2023年春季北师版数学九年级下册第二章《二次函数》单元检测B

试卷更新日期：2022-11-18 类型：单元试卷

进入出卷网下载

一、单选题（每题3分，共30分）

1. 二次函数 $y = x^{2} + 2 x + 2$ 的图象的对称轴是（）

A、 $x = - 1$ B、 $x = - 2$ C、 $x = 1$ D、 $x = 2$

查看试题解析
2. 抛物线的函数表达式为y＝（x﹣2）²﹣9，则下列结论中，正确的序号为（　　）
①当x＝2时，y取得最小值﹣9；②若点（3，y₁），（4，y₂）在其图象上，则y₂＞y₁；③将其函数图象向左平移3个单位长度，再向上平移4个单位长度所得抛物线的函数表达式为y＝（x﹣5）²﹣5；④函数图象与x轴有两个交点，且两交点的距离为6.

A、②③④ B、①②④ C、①③ D、①②③④

查看试题解析
3. 已知二次函数y=x²−2x−3的自变量x₁ ， x₂ ， x₃对应的函数值分别为y₁ ， y₂ ， y₃.当−1<x₁<0，1<x₂<2，x₃>3时，y₁ ， y₂ ， y₃三者之间的大小关系是（）

A、 $y_{1} < y_{2} < y_{3}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{3} < y_{1} < y_{2}$ D、 $y_{2} < y_{3} < y_{1}$

查看试题解析
4. 已知抛物线 $y = (x - 2)^{2} + 1$ ，下列结论错误的是（）

A、抛物线开口向上 B、抛物线的对称轴为直线 $x = 2$ C、抛物线的顶点坐标为 $(2 ， 1)$ D、当 $x < 2$ 时，y随x的增大而增大

查看试题解析
5. 已知抛物线 y=x²+mx的对称轴为直线 x=2 ，则关于x的方程 x²+mx=5的根是（）

A、0，4 B、1，5 C、1，－5 D、－1，5

查看试题解析
6. 在平面直角坐标系中，将二次函数 $y = x^{2}$ 的图象向左平移2个单位长度，再向上平移1个单位长度，所得抛物线对应的函数表达式为（）

A、 $y = {(x - 2)}^{2} + 1$ B、 $y = {(x + 2)}^{2} + 1$ C、 $y = {(x + 2)}^{2} - 1$ D、 $y = {(x - 2)}^{2} - 1$

查看试题解析
7. 小嘉说：将二次函数 $y = x^{2}$ 的图象平移或翻折后经过点 $(2 ， 0)$ 有4种方法：
①向右平移2个单位长度 ②向右平移1个单位长度，再向下平移1个单位长度③向下平移4个单位长度④沿x轴翻折，再向上平移4个单位长度

你认为小嘉说的方法中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 在平面直角坐标系中，已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象如图所示，有下列5个结论：① $a b c > 0$ ；② $2 a - b = 0$ ；③ 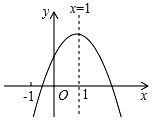$9 a + 3 b + c > 0$ ；④ $b^{2} > 4 a c$ ；⑤ $a + c < b$ .其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 如图，抛物线y＝ax²+bx+c（a≠0）与x轴交于点A（5，0），与y轴交于点C，其对称轴为直线x＝2，结合图象分析如下结论：①abc＞0；②b+3a＜0；③当x＞0时，y随x的增大而增大；④若一次函数y＝kx+b（k≠0）的图象经过点A，则点E（k，b）在第四象限；⑤点M是抛物线的顶点，若CM⊥AM，则a＝ $\frac{\sqrt{6}}{6}$ ．其中正确的有（）

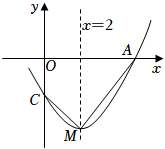A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象的一部分与x轴的一个交点坐标为 $(1 ， 0)$ ，对称轴为 $x = - 1$ ，结合图象给出下列结论：

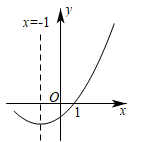
① $a + b + c = 0$ ；

② $a - 2 b + c < 0$ ；

③关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两根分别为-3和1；

④若点 $(- 4 ， y_{1})$ ， $(- 2 ， y_{2})$ ， $(3 ， y_{3})$ 均在二次函数图象上，则 $y_{1} < y_{2} < y_{3}$ ；

⑤ $a - b < m (a m + b)$ （m为任意实数）．

其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题（每题3分，共18分）

11. 如图，以一定的速度将小球沿与地面成一定角度的方向击出时，小球的飞行路线是一条抛物线.若不考虑空气阻力，小球的飞行高度 $h$ （单位：m）与飞行时间 $t$ （单位：s）之间具有函数关系： $h = - 5 t^{2} + 20 t$ ，则当小球飞行高度达到最高时，飞行时间 $t =$ s.

查看试题解析
12. 抛物线y＝ax²+bx+c（a，b，c为常数）的部分图象如图所示，设m＝a﹣b+c，则m的取值范围是 .

查看试题解析
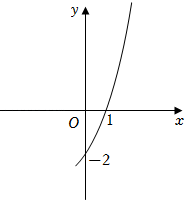13. 某超市购进一批单价为8元的生活用品，如果按每件9元出售，那么每天可销售20件．经调查发现，这种生活用品的销售单价每提高1元，其销售量相应减少4件，那么将销售价定为元时，才能使每天所获销售利润最大．

查看试题解析
14. 抛物线y＝ax²+bx+c（a，b，c为常数，a＞0）经过（0，0），（4，0）两点.则下列四个结论正确的有（填写序号）.
①4a+b＝0；

②5a+3b+2c＞0；

③若该抛物线y＝ax²+bx+c与直线y＝﹣3有交点，则a的取值范围是a $\geq \frac{3}{4}$ ；

④对于a的每一个确定值，如果一元二次方程ax²+bx+c﹣t＝0（t为常数，t≤0）的根为整数，则t的值只有3个.

查看试题解析
15. 以初速度v（单位：m/s）从地面竖直向上抛出小球，从抛出到落地的过程中，小球的高度h（单位：m）与小球的运动时间t（单位：s）之间的关系式是h＝vt﹣4.9t².现将某弹性小球从地面竖直向上抛出，初速度为v₁ ，经过时间t₁落回地面，运动过程中小球的最大高度为h₁（如图1）；小球落地后，竖直向上弹起，初速度为v₂ ，经过时间t₂落回地面，运动过程中小球的最大高度为h₂（如图2）.若h₁＝2h₂ ，则t₁：t₂＝.

查看试题解析
16. 已知二次函数 $y = a x^{2} + b x + c (a \neq 0)$ ，图象的一部分如图所示，该函数图象经过点 $(- 2 ， 0)$ ，对称轴为直线 $x = - \frac{1}{2}$ .对于下列结论：① $a b c < 0$ ；② $b^{2} - 4 a c > 0$ ；③ $a + b + c = 0$ ；④ $a m^{2} + b m < \frac{1}{4} (a - 2 b)$ （其中 $m \neq - \frac{1}{2}$ ）；⑤若 $A (x_{1} ， y_{1})$ 和 $B (x_{2} ， y_{2})$ 均在该函数图象上，且 $x_{1} > x_{2} > 1$ ，则 $y_{1} > y_{2}$ .其中正确结论的个数共有个.

查看试题解析

三、解答题（共8题，共72分）

17. 某文具店购进一批单价为12元的学习用品，按照相关部门规定其销售单价不低于进价，且不高于进价的1.5倍，通过分析销售情况，发现每天的销售量y（件）与销售单价x（元）满足一次函数关系，且当 $x = 15$ 时， $y = 50$ ；当 $x = 17$ 时， $y = 30$ ．

(1)、求y与x之间的函数关系式；

(2)、这种学习用品的销售单价定为多少时，每天可获得最大利润，最大利润是多少元？

查看试题解析
18. 小红看到一处喷水景观，喷出的水柱呈抛物线形状，她对此展开研究：测得喷水头P距地面0.7m，水柱在距喷水头P水平距离5m处达到最高，最高点距地面3.2m；建立如图所示的平面直角坐标系，并设抛物线的表达式为 $y = a {(x - h)}^{2} + k$ ，其中x（m）是水柱距喷水头的水平距离，y（m）是水柱距地面的高度.

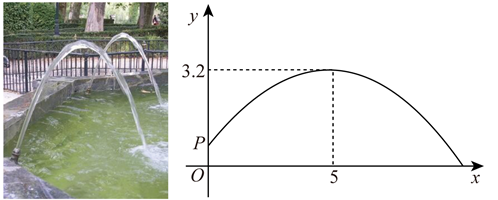(1)、求抛物线的表达式.

(2)、爸爸站在水柱正下方，且距喷水头P水平距离3m，身高1.6m的小红在水柱下方走动，当她的头顶恰好接触到水柱时，求她与爸爸的水平距离.

查看试题解析

19. “八婺”菜场指导菜农生产和销售某种蔬菜，提供如下信息：

①统计售价与需求量的数据，通过描点(图1)，发现该蔬菜需求量y_需求(吨)关于售价x(元/千克)的函数图象可以看成抛物线，其表达式为 $y_{需求} = a x^{2} + c$ ，部分对应值如下表：

售价x(元/千克)	…	2.5	3	3.5	4	…
需求量y_需求(吨）	…	7.75	7.2	6.55	5.8	…

②该蔬菜供给量y_供给(吨)关于售价x(元/千克)的函数表达式为y_供给=x-1，函数图象见图1.

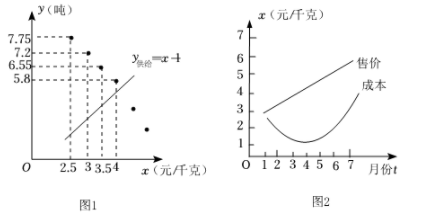
③1~7月份该蔬菜售价x_售价(元/千克)、成本x_成本(元/千克)关于月份t的函数表达式分别为 $x_{售价} = \frac{1}{2} t + 2$ ， $x_{成本} = \frac{1}{4} t^{2} - \frac{3}{2} t + 3$ ，函数图象见图2.

请解答下列问题：

(1)、求a，c的值.

(2)、根据图2，哪个月出售这种蔬菜每千克获利最大？并说明理由.

(3)、求该蔬菜供给量与需求量相等时的售价，以及按此价格出售获得的总利润.

查看试题解析

20. 已知抛物线经过A（－1，0）、B（0、3）、 C（3，0）三点，O为坐标原点，抛物线交正方形OBDC的边BD于点E，点M为射线BD上一动点，连接OM ，交BC于点F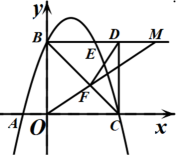

(1)、求抛物线的表达式；

(2)、求证：∠BOF＝∠BDF ：

(3)、是否存在点M使△MDF为等腰三角形？若不存在，请说明理由；若存在，求ME的长

查看试题解析
21. 如图，抛物线 $y = a x^{2} + b x + c$ 与 $x$ 轴交于 $A (3 ， 0)$ 、 $B (- 1 ， 0)$ 两点，与 $y$ 轴交于点 $C (0 ， 3)$ ，其顶点为点 $D$ ，连结 $A C$ .

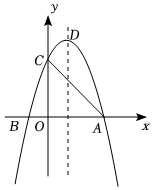(1)、求这条抛物线所对应的二次函数的表达式及顶点 $D$ 的坐标；

(2)、在抛物线的对称轴上取一点 $E$ ，点 $F$ 为抛物线上一动点，使得以点 $A$ 、 $C$ 、 $E$ 、 $F$ 为顶点、 $A C$ 为边的四边形为平行四边形，求点 $F$ 的坐标；

(3)、在（2）的条件下，将点 $D$ 向下平移5个单位得到点 $M$ ，点 $P$ 为抛物线的对称轴上一动点，求 $P F + \frac{3}{5} P M$ 的最小值.

查看试题解析
22. 如图，在平面直角坐标系xOy中，抛物线E：y＝﹣（x﹣m）²+2m²（m＜0）的顶点P在抛物线F：y＝ax²上，直线x＝t与抛物线E，F分别交于点A，B．

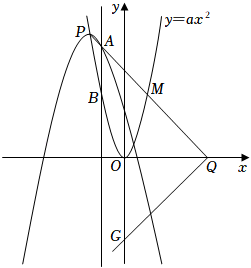(1)、求a的值；

(2)、将A，B的纵坐标分别记为yA，yB，设s＝yA﹣yB，若s的最大值为4，则m的值是多少？

(3)、Q是x轴的正半轴上一点，且PQ的中点M恰好在抛物线F上．试探究：此时无论m为何负值，在y轴的负半轴上是否存在定点G，使∠PQG总为直角？若存在，请求出点G的坐标；若不存在，请说明理由．

查看试题解析
23. 已知二次函数图象的顶点坐标为 $A (1 ， 4)$ ，且与x轴交于点 $B (- 1 ， 0)$ ．

(1)、求二次函数的表达式；

(2)、如图，将二次函数图象绕x轴的正半轴上一点 $P (m ， 0)$ 旋转 $180 °$ ，此时点A、B的对应点分别为点C、D．
①连结 $A B 、 B C 、 C D 、 D A$ ，当四边形 $A B C D$ 为矩形时，求m的值；
②在①的条件下，若点M是直线 $x = m$ 上一点，原二次函数图象上是否存在一点Q，使得以点B、C、M、Q为顶点的四边形为平行四边形，若存在，求出点Q的坐标；若不存在，请说明理由．

查看试题解析
24. 【生活情境】
为美化校园环境，某学校根据地形情况，要对景观带中一个长 $A D = 4 m$ ，宽 $A B = 1 m$ 的长方形水池 $A B C D$ 进行加长改造（如图①，改造后的水池 $A B N M$ 仍为长方形，以下简称水池1），同时，再建造一个周长为 $12 m$ 的矩形水池 $E F G H$ （如图②，以下简称水池2）．
【建立模型】
如果设水池 $A B C D$ 的边 $A D$ 加长长度 $D M$ 为 $x (m) (x > 0)$ ，加长后水池1的总面积为 $y_{1} (m^{2})$ ，则 $y_{1}$ 关于 $x$ 的函数解析式为： $y_{1} = x + 4 (x > 0)$ ；设水池2的边 $E F$ 的长为 $x (m) (0 < x < 6)$ ，面积为 $y_{2} (m^{2})$ ，则 $y_{2}$ 关于 $x$ 的函数解析式为： $y_{2} = - x^{2} + 6 x (0 < x < 6)$ ，上述两个函数在同一平面直角坐标系中的图像如图③．
【问题解决】

(1)、若水池2的面积随 $E F$ 长度的增加而减小，则 $E F$ 长度的取值范围是（可省略单位），水池2面积的最大值是 $m^{2}$ ；

(2)、在图③字母标注的点中，表示两个水池面积相等的点是，此时的 $x (m)$ 值是；

(3)、当水池1的面积大于水池2的面积时， $x (m)$ 的取值范围是；

(4)、在 $1 < x < 4$ 范围内，求两个水池面积差的最大值和此时 $x$ 的值；

(5)、假设水池 $A B C D$ 的边 $A D$ 的长度为 $b (m)$ ，其他条件不变（这个加长改造后的新水池简称水池3），则水池3的总面积 $y_{3} (m^{2})$ 关于 $x (m) (x > 0)$ 的函数解析式为： $y_{3} = x + b (x > 0)$ ．若水池3与水池2的面积相等时， $x (m)$ 有唯一值，求 $b$ 的值．

查看试题解析

2023年春季北师版数学九年级下册第二章 《二次函数》单元检测B

一、单选题（每题3分，共30分）

二、填空题（每题3分，共18分）

三、解答题（共8题，共72分）

2023年春季北师版数学九年级下册第二章《二次函数》单元检测B