内蒙古自治区通辽市科尔沁区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-11-18 类型:期末考试
一、单选题
-
1. 如图图形是以科学家名字命名的,其中是轴对称图形的有( )
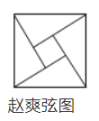


 A、1个 B、2个 C、3个 D、4个2. 用木棒钉成一个三角架,两根小棒分别是7cm和10cm,第三根小棒可取( )A、20cm B、3cm C、11cm D、2cm3. 华为 手机搭载了全球首款7纳米制程芯片,7纳米就是0.000000007米.数据0.000000007用科学记数法表示为( ).A、 B、 C、 D、4. 下面运算中正确的是( )A、 B、 C、 D、5. 如图,已知BC=BD,那么添加下列一个条件后,仍无法判定△ABC≌△ABD的是( )
A、1个 B、2个 C、3个 D、4个2. 用木棒钉成一个三角架,两根小棒分别是7cm和10cm,第三根小棒可取( )A、20cm B、3cm C、11cm D、2cm3. 华为 手机搭载了全球首款7纳米制程芯片,7纳米就是0.000000007米.数据0.000000007用科学记数法表示为( ).A、 B、 C、 D、4. 下面运算中正确的是( )A、 B、 C、 D、5. 如图,已知BC=BD,那么添加下列一个条件后,仍无法判定△ABC≌△ABD的是( ) A、AC=AD B、∠ABC=∠ABD C、∠C=∠D=90° D、∠CAB=∠DAB6. 下列各式由左边到右边的变形中,是因式分解的为( )A、a(x+y)=ax+ay B、10x2﹣5x=5x(2x﹣1) C、x2﹣4x+4=(x﹣4)2 D、x2﹣16+3x=(x+4)(x﹣4)+3x7. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、过C作EF AB
A、AC=AD B、∠ABC=∠ABD C、∠C=∠D=90° D、∠CAB=∠DAB6. 下列各式由左边到右边的变形中,是因式分解的为( )A、a(x+y)=ax+ay B、10x2﹣5x=5x(2x﹣1) C、x2﹣4x+4=(x﹣4)2 D、x2﹣16+3x=(x+4)(x﹣4)+3x7. 在探究证明“三角形的内角和是180°”时,综合实践小组的同学作了如下四种辅助线,其中不能证明“三角形内角和是180°”的是( )A、过C作EF AB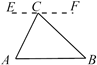 B、过AB上一点D作DE BC,DF AC
B、过AB上一点D作DE BC,DF AC 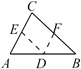 C、延长AC到F,过C作CE AB
C、延长AC到F,过C作CE AB  D、作CD⊥AB于点D
D、作CD⊥AB于点D 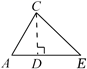 8. 已知: , 则的值是( )A、 B、 C、5 D、9. 下列各式从左到右变形正确的是( )A、 B、 C、 D、10. 如图,已知的内角 , 分别作内角与外角的平分线,两条平分线交于点 , 得;和的平分线交于点 , 得;……以此类推得到 , 则的度数是( )
8. 已知: , 则的值是( )A、 B、 C、5 D、9. 下列各式从左到右变形正确的是( )A、 B、 C、 D、10. 如图,已知的内角 , 分别作内角与外角的平分线,两条平分线交于点 , 得;和的平分线交于点 , 得;……以此类推得到 , 则的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分式有意义的条件是.12. 十二边形的内角和是13. 如图,在 中, , ,DE垂直平分AC,交BC于点E, ,则 .
 14. 若等腰三角形一个内角是70°,则该三角形的顶角为 .15. 如图, , , , 为上一动点,则的最小值为 .
14. 若等腰三角形一个内角是70°,则该三角形的顶角为 .15. 如图, , , , 为上一动点,则的最小值为 . 16. 《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为.17. 的结果是 .
16. 《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为.17. 的结果是 .三、解答题
-
18. 计算:(1)、;(2)、 .19. 解方程:(1)、;(2)、 .20. 如图1所示的折叠凳.图2是折叠凳撑开后的侧面示意图(木条等材料宽度忽略不计),其中凳腿和的长相等,是它们的中点.为了使折叠凳坐着舒适,厂家将撑开后的折叠凳宽度设计为 , 则由以上信息求的长度.
 21. 先化简,再求值: , 其中满足 .22. 如图,已知 , , .
21. 先化简,再求值: , 其中满足 .22. 如图,已知 , , .
( 1 )作关于轴对称的;
( 2 )在轴上找一点使得最小,画出点所在的位置;
( 3 )求的面积.
23. 某单位在疫情期间用6000元购进、两种口罩1100个,购买种口罩与购买种口罩的费用相同,且种口罩的单价是种口罩单价的1.2倍;(1)、求 , 两种口罩的单价各是多少元?(2)、随着口罩供应量不断充足,、两种口罩的进价都下降了 , 若计划用不超过9000元的资金再次购进、两种口罩共2800个,求种口罩最多能购进多少个?24. 如图1,在平面直角坐标系中,的顶点、 , 点在轴正半轴上,点 , 的延长线交于点 , 且 . (1)、求点的坐标;(2)、判断与的位置关系,并说明理由;(3)、如图2,求证:平分 .25. 阅读材料:利用公式法,可以将一些形如()的多项式变形为的形式,我们把这样的变形方法叫做多项式()的配方法,运用多项式的配方法可以解决一些数学问题.比如运用多项式的配方法及平方差公式能对一些多项式进行因式分解.
(1)、求点的坐标;(2)、判断与的位置关系,并说明理由;(3)、如图2,求证:平分 .25. 阅读材料:利用公式法,可以将一些形如()的多项式变形为的形式,我们把这样的变形方法叫做多项式()的配方法,运用多项式的配方法可以解决一些数学问题.比如运用多项式的配方法及平方差公式能对一些多项式进行因式分解.例: .
.
根据以上材料,利用多项式的配方解答下列问题.
(1)、分解因式:;(2)、求多项式的最小值;(3)、已知 , , 是的三边长,且满足 , 求的周长.26. 【问题背景】在四边形中, , , , , 分别是 , 上的点,且 , 试探究图中线段 , , 之间的数量关系.(1)、【初步探索】读图一,小亮同学认为:延长到点 , 使 , 连接 , 先证明 , 再证明 , 则可得到 , , 之间的数量关系是 . (2)、【探索延伸】在图二四边形中, , , , 分别是 , 上的点, , 上述结论是否仍然成立?说明理由.
(2)、【探索延伸】在图二四边形中, , , , 分别是 , 上的点, , 上述结论是否仍然成立?说明理由. (3)、【结论运用】如图三,在某次军事演习中,舰艇甲在指挥中心(处)北偏西的处,舰艇乙在指挥中心南偏东的处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以海里/小时的速度前进,舰艇乙沿北偏东的方向以海里/小时的速度前进小时后,指挥中心观测到甲、乙两舰艇分别到达 , 处,且两舰艇之间的夹角()为 , 试求此时两舰艇之间的距离.
(3)、【结论运用】如图三,在某次军事演习中,舰艇甲在指挥中心(处)北偏西的处,舰艇乙在指挥中心南偏东的处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以海里/小时的速度前进,舰艇乙沿北偏东的方向以海里/小时的速度前进小时后,指挥中心观测到甲、乙两舰艇分别到达 , 处,且两舰艇之间的夹角()为 , 试求此时两舰艇之间的距离.