内蒙古自治区呼和浩特市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-11-18 类型:期末考试
一、单选题
-
1. 下列四个图案中,不是轴对称图形的是( )A、
 B、
B、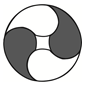 C、
C、 D、
D、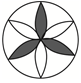 2. 下列各式: , , , , , 中,是分式的共有( )A、1个 B、2个 C、3个 D、4个3. 新冠病毒的大小为125纳米也就是0.000000125米,这个数据用科学记数法可表示为( )A、0.125×107 B、1.25×107 C、1.25×10-7 D、0.125×10-74. 下列各式运算正确的是( )A、 B、 C、 D、5. 某多边形的内角和比外角和多180度,这个多边形的边数( )A、3 B、4 C、5 D、66. -的计算结果为( )A、 B、 C、 D、7. 下列命题:①等腰三角形的角平分线、底边中线、高线三线合一;②有一个外角等于120°的等腰三角形是等边三角形;③等腰三角形的一边长为3,另一边为7,则它的周长为13或17;④轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.其中正确的有( )A、1个 B、2个 C、3个 D、4个8. 已知a2+b2=2a-b-2,则a-b的值为( )A、-1 B、-2 C、1 D、3
2. 下列各式: , , , , , 中,是分式的共有( )A、1个 B、2个 C、3个 D、4个3. 新冠病毒的大小为125纳米也就是0.000000125米,这个数据用科学记数法可表示为( )A、0.125×107 B、1.25×107 C、1.25×10-7 D、0.125×10-74. 下列各式运算正确的是( )A、 B、 C、 D、5. 某多边形的内角和比外角和多180度,这个多边形的边数( )A、3 B、4 C、5 D、66. -的计算结果为( )A、 B、 C、 D、7. 下列命题:①等腰三角形的角平分线、底边中线、高线三线合一;②有一个外角等于120°的等腰三角形是等边三角形;③等腰三角形的一边长为3,另一边为7,则它的周长为13或17;④轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.其中正确的有( )A、1个 B、2个 C、3个 D、4个8. 已知a2+b2=2a-b-2,则a-b的值为( )A、-1 B、-2 C、1 D、3二、填空题
-
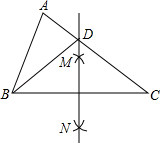
9. 当时,分式的值为0.10. 如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于BC的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD.若AC=6,AD=2,则BD的长为 .
 11. 若an=3,bn=4,则 (ab)2n= .12. 图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,得到四块形状和大小完全相同的小长方形,然后按图(2)所示拼成一个大正方形,则中间空白部分的面积是 . (用含a,b的式子表示)
11. 若an=3,bn=4,则 (ab)2n= .12. 图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,得到四块形状和大小完全相同的小长方形,然后按图(2)所示拼成一个大正方形,则中间空白部分的面积是 . (用含a,b的式子表示)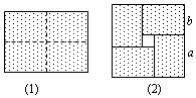 13. 方程 的解是 .14. 如图,在△ABC中,O是△ABC内一点,且点O到△ABC三边的距离相等,∠BOC=126°,则∠A的度数为 .
13. 方程 的解是 .14. 如图,在△ABC中,O是△ABC内一点,且点O到△ABC三边的距离相等,∠BOC=126°,则∠A的度数为 .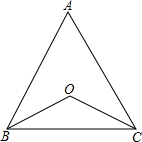 15. 如图,等边△ABC中,BD⊥AC于D,QD=1.5,点P、Q分别为AB、AD上的两个定点且BP=AQ=2,在BD上有一动点E使PE+QE最短,则PE+QE的最小值为 .
15. 如图,等边△ABC中,BD⊥AC于D,QD=1.5,点P、Q分别为AB、AD上的两个定点且BP=AQ=2,在BD上有一动点E使PE+QE最短,则PE+QE的最小值为 . 16. 下面三个判断:①顶角及一个底角的角平分线长对应相等的两个等腰三角形全等;②如果等腰三角形的一个外角是80°,则另外两个角一定都等于40°;③如果两个三角形全等、则它们必是关于某条直线成轴对称的图形.④若两个直角三角形斜边上的中线相等,则这两个直角三角形全等.其中正确的判断有(填序号即可).
16. 下面三个判断:①顶角及一个底角的角平分线长对应相等的两个等腰三角形全等;②如果等腰三角形的一个外角是80°,则另外两个角一定都等于40°;③如果两个三角形全等、则它们必是关于某条直线成轴对称的图形.④若两个直角三角形斜边上的中线相等,则这两个直角三角形全等.其中正确的判断有(填序号即可).三、解答题
-
17.(1)、计算:(x2+2x+3)(2x-5);(2)、因式分解:a4-1;(3)、先化简,再求值:[(x-2y)2+(x-2y)(x+2y)-2x(2x-y)]÷2x,其中x=1,y=-218. 解方程: .19. 如图,已知AC⊥BC,BD⊥AD,AC与BD交于点O,AC=BD.
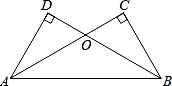 (1)、求证:△OAB是等腰三角形;(2)、若∠CBA=60°,求证AC=3OC.20. 如图,在平面直角坐标系xOy中,△ABC三个顶点分别在边长为1的格点上.
(1)、求证:△OAB是等腰三角形;(2)、若∠CBA=60°,求证AC=3OC.20. 如图,在平面直角坐标系xOy中,△ABC三个顶点分别在边长为1的格点上.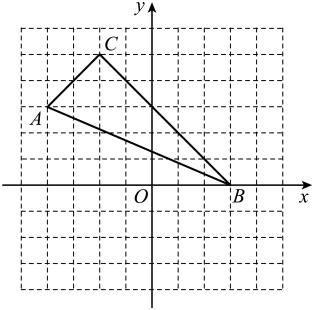 (1)、作出△ABC关于y轴对称的△A1B1C1;(2)、在x轴上找出一个点P,使点P到B、C两点的距离相等,则点P的坐标为 .21. 如图,△ABC中,AB=AC,E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.
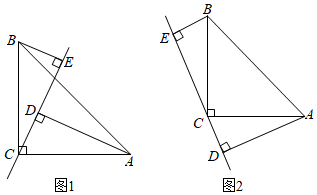
(1)、作出△ABC关于y轴对称的△A1B1C1;(2)、在x轴上找出一个点P,使点P到B、C两点的距离相等,则点P的坐标为 .21. 如图,△ABC中,AB=AC,E在线段AC上,D在AB的延长线上,连接DE交BC于F,过E作EG⊥BC于G.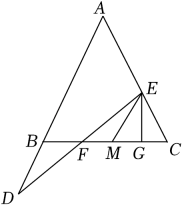 (1)、若∠A=50°,∠D=20°,求证△EFG是等腰直角三角形;(2)、若BD=CE,EM∥AD,M在BC上,求证:点F是BM的中点.22. “杂交水稻之父”袁隆平团队示范基地的“水稻1号”的试验田是边长为a米(a>1)的正方形去掉一个边长为1米的正方形蓄水池后余下的部分,“水稻2号”的试验田是边长为(a-1)米的正方形,两块试验田的水稻都收获了1000千克.(1)、试说明哪种水稻的单位面积产量高?(2)、高的单位面积产量是低的单位面积产量的多少倍?23. 已知△ABC中,∠ACB=90°,AC=BC.BE、AD分别与过点C的直线垂直,且垂足分别为D,E.
(1)、若∠A=50°,∠D=20°,求证△EFG是等腰直角三角形;(2)、若BD=CE,EM∥AD,M在BC上,求证:点F是BM的中点.22. “杂交水稻之父”袁隆平团队示范基地的“水稻1号”的试验田是边长为a米(a>1)的正方形去掉一个边长为1米的正方形蓄水池后余下的部分,“水稻2号”的试验田是边长为(a-1)米的正方形,两块试验田的水稻都收获了1000千克.(1)、试说明哪种水稻的单位面积产量高?(2)、高的单位面积产量是低的单位面积产量的多少倍?23. 已知△ABC中,∠ACB=90°,AC=BC.BE、AD分别与过点C的直线垂直,且垂足分别为D,E.学习完第十二章后,张老师首先让同学们完成问题1:如图1,若AD=2.5cm,DE=1.7cm,求BE的长;然后,张老师又提出问题2:将图1中的直线CE绕点C旋转到△ABC的外部,BE、AD与直线CE的垂直关系不变,如图2,猜想AD、DE、BE三者的数量关系,并给予证明.
 24. 甲、乙两公司全体员工踊跃参与“携手防疫,共渡难关”捐款活动,甲公司共捐款100000元,乙公司共捐款140000元.下面是甲、乙两公司员工的一段对话:
24. 甲、乙两公司全体员工踊跃参与“携手防疫,共渡难关”捐款活动,甲公司共捐款100000元,乙公司共捐款140000元.下面是甲、乙两公司员工的一段对话: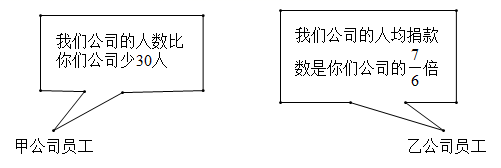 (1)、甲、乙两公司各有多少人?(2)、现甲、乙两公司共同使用这笔捐款购买 、 两种防疫物资, 种防疫物资每箱15000元, 种防疫物资每箱12000元.若购买 种防疫物资不少于10箱,并恰好将捐款用完,有几种购买方案?请设计出来(注: 、 两种防疫物资均需购买,并按整箱配送).
(1)、甲、乙两公司各有多少人?(2)、现甲、乙两公司共同使用这笔捐款购买 、 两种防疫物资, 种防疫物资每箱15000元, 种防疫物资每箱12000元.若购买 种防疫物资不少于10箱,并恰好将捐款用完,有几种购买方案?请设计出来(注: 、 两种防疫物资均需购买,并按整箱配送).