内蒙古自治区鄂尔多斯市准格尔旗2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-11-18 类型：期末考试

进入出卷网下载

一、单选题

1. 下列科学防控“新冠肺炎”的图片中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 中国药学家屠呦呦获2015年诺贝尔医学奖，她的突出贡献是创制新型抗疟药青蒿素和双氢青蒿素，这是中国医学界迄今为止获得的最高奖项，已知显微镜下某种疟原虫平均长度为0.0000015米，该长度用科学记数法可表示为（）

A、 $1.5 \times 10^{- 6}$ 米 B、 $1.5 \times 10^{- 5}$ 米 C、 $1.5 \times 10^{6}$ 米 D、 $1.5 \times 10^{5}$ 米

查看试题解析
3. 将一副三角板如图放置，若 $A E$ // $B C$ ，则 $∠ A F D$ 的度数为（）

A、85° B、75° C、45° D、15°

查看试题解析
4. 下面运算中正确的是（）

A、 $m^{2} \cdot m^{3} = m^{6}$ B、 $m^{2} + m^{2} = 2 m^{4}$ C、 $(- 3 a^{2} b)^{2} = 6 a^{4} b^{2}$ D、 $(- 2 x^{2}) \cdot (- 5 x^{4}) = 10 x^{6}$

查看试题解析
5. 若一个多边形的内角和是外角和的2倍，则此多边形是（）

A、三角形 B、四边形 C、六边形 D、八边形

查看试题解析
6. 下列各式中，从左到右的变形是因式分解的是（）

A、 $6 x^{7} = 3 x^{2} \cdot 2 x^{5}$ B、 $3 x + 3 y - 5 = 3 (x + y) - 5$ C、 $4 x^{2} + 4 x = 4 x (x + 1)$ D、 $(x + 1) (x - 1) = x^{2} - 1$

查看试题解析
7. 如图，在 $△$ ABC中，分别以点A和点B为圆心，大于 $\frac{1}{2} A B$ 长为半径画弧，两弧相交于点M，N，作直线MN，交BC于点D，交AB于点E，连接AD．若 $△$ ADC的周长为12， $△$ ABC的周长为20，则AE的长为（）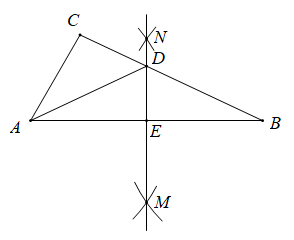

A、12 B、4 C、20 D、8

查看试题解析
8. 若关于x的分式方程 $\frac{x + a}{x - 3} + \frac{2 a}{3 - x} = \frac{1}{3}$ 的解是非负数，则a的取值范围为（）

A、a＞1 B、a≥1 C、a≥1且a≠3 D、a＞1且a≠3

查看试题解析
9. 在△ABC中，已知点D、E、F分别是BC、AD、CE的中点，且S_△ABC=4 cm² ，则S_△BEF=（　　）

A、2 cm² B、1cm² C、0.5cm² D、0.25 cm²

查看试题解析
10. 如图，已知 $△ A B C$ 和 $△ C D E$ 都是等边三角形，点B、C、D在同一条直线上，BE交AC于点M，AD交CE于点N，AD，BE交于点P．则下列结论：① $A D = B E$ ；② $∠ B M C = ∠ A N C$ ；③ $∠ A P M = 60 °$ ；④ $A N = B M$ ；⑤ $△ C M N$ 是等边三角形、其中，正确的有（）

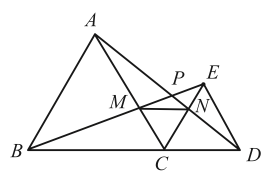A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

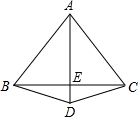
11. 若分式 $\frac{3}{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
12. 若 $m^{2} + m - 1 = 0$ ，则 $m^{3} + 2 m^{2} + 2021 =$ ．

查看试题解析
13. 如图，AB=AC=4cm，DB＝DC，若∠ABC为60°，则BE为．

查看试题解析
14. 如图，在 $△ A B C$ 中，D在AC上，连接BD，且 $∠ A B C = ∠ C = ∠ B D C$ ， $∠ A = ∠ A B D$ ，则 $∠ A$ 的度数为度．

查看试题解析
15. 如图，等腰三角形ABC的底边BC长为4，面积是16，腰AC的垂直平分线EF分别交AC，AB边于E，F点，若点D为BC边的中点，点M为线段EF上一动点，则 $△ CDM$ 周长的最小值为.

查看试题解析
16. 如图，已知 $∠ M O N = 30 °$ ，点 $A_{1}$ ， $A_{2}$ ， $A_{3} ，$ ， …在射线ON上，点 $B_{1}$ ， $B_{2}$ ， $B_{3}$ ， …在射线OM上， $△ A_{1} B_{1} A_{2}$ ， $△ A_{2} B_{2} A_{3}$ ， $△ A_{3} B_{3} A_{4}$ ， …均为等边三角形，若 $O A_{1} = 2$ ，则 $△ A_{2022} B_{2022} A_{2023}$ 的边长为．

查看试题解析

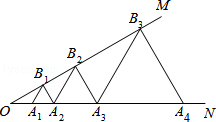
三、解答题

17.

(1)、计算： $\sqrt{9} - {(3.14 - π)}^{0} + {(\frac{1}{5})}^{- 1}$ ；

(2)、计算： $(a^{2} b - 2 a b^{2} - b^{3}) \div b - (a + b) (a - b)$ ；

(3)、分解因式： $3 x^{3} - 27 x$ ；

(4)、解方程： $\frac{x + 1}{x - 1} - \frac{4}{x^{2} - 1} = 1$ ．

查看试题解析
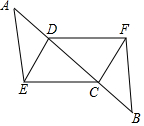
18. 先化简： $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4 x + 4}{x^{2} - 1}$ ，再从 $- 1 \leq x \leq 2$ 的范围内选取一个合适的整数作为 $x$ 的值代入求值.

查看试题解析
19. 已知：如图，点A、D、C、B在同一条直线上，AD=BC，AE=BF，CE=DF，求证：AE∥BF．

查看试题解析
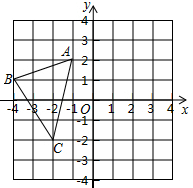
20. 如图所示的坐标系中，△ABC的三个顶点的坐标依次为A（-1，2），B（-4，1），C（-2，-2）
（ 1 ）请在这个坐标系中作出△ABC关于y轴对称的△A₁B₁C₁；
（ 2 ）分别写出A₁、B₁、C₁的坐标；
（ 3 ）求△ABC的面积．

查看试题解析
21. 如图， $△ A B C$ 为等边三角形，点D，E分别在BC，AC边上，且 $A E = C D$ ， AD与BE相交于点F， $B G ⊥ A D$ ，垂足为G．

(1)、求证： $A D = B E$ ；

(2)、若 $B F = 4$ ，求FG的长．

查看试题解析
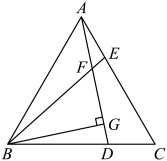22. 铭润超市用5000元购进一批新品种的苹果进行试销，由于销售状况良好，超市又调拨11000元资金购进该品种苹果，但这次的进货价比试销时每千克多了0.5元，购进苹果数量是试销时的2倍．

(1)、试销时该品种苹果的进货价是每千克多少元？

(2)、如果超市将该品种苹果按每千克7元的定价出售，当大部分苹果售出后，余下的400千克按定价的七折（“七折”即定价的70%）售完，那么超市在这两次苹果销售中共盈利多少元？

查看试题解析
23. 阅读材料：若m²﹣2mn+2n²﹣10n+25＝0，求m ， n的值．
解：∵m²﹣2mn+2n²﹣10n+25＝0，

∴（m²﹣2mn+n²）+（n²﹣10n+25）＝0．

∴（m﹣n）²+（n﹣5）²＝0，

∴m﹣n＝0，n﹣5＝0．

∴n＝5，m＝5．

根据你的观察，探究下面的问题：

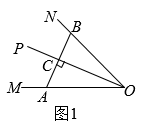
(1)、已知：x²+2xy+2y²+4y+4＝0，求x^y的值；

(2)、已知：△ABC的三边长a ， b ， c都是正整数，且满足：a²+b²﹣16a﹣12b+100＝0，求△ABC的周长的最大值；

(3)、已知：△ABC的三边长是a ， b ， c ，且满足：a²+2b²+c²﹣2b（a+c）＝0，试判断△ABC是什么形状的三角形并说明理由．

查看试题解析
24. 【问题情境】
利用角平分线构造全等三角形是常用的方法，如图1，OP平分 $∠ M O N$ ．点A为OM上一点，过点A作 $A C ⊥ O P$ ，垂足为C，延长AC交ON于点B，可根据ASA证明 $△ A O C ≅ △ B O C$ ，则 $A O = B O$ ， $A C = B C$ （即点C为AB的中点）．

(1)、问题探究：如图2， $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ， CD平分 $∠ A C B$ ， $B E ⊥ C D$ ，垂足E在CD的延长线上，试探究BE和CD的数量关系，并证明你的结论：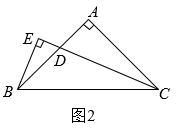

(2)、拓展延伸：如图3， $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 90 °$ ，点D在线段BC上，且 $∠ B D E = \frac{1}{2} ∠ A C B$ ， $B E ⊥ D E$ 于E，DE交AB于F，试探究BE和DF之间的数量关系，并证明你的结论．

查看试题解析