内蒙古自治区包头市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-11-18 类型:期末考试
一、单选题
-
1. 4的平方根是( )A、4 B、±4 C、±2 D、22. 在平面直角坐标系的第二象限内有一点P,点P到x轴的距离为2,到y轴的距离为3,则点P的坐标是( )A、 B、 C、 D、3. 李老师为了解学生每周参加家务劳动的时间,随机调查了本班7名学生,收集到如下数据(单位:小时):4,3,6,5,5,4,5,则这组数据的中位数和众数分别是( )A、5,5 B、5,4 C、4,5 D、5,64. 一次函数在平面直角坐标系内的大致图象是( )A、
 B、
B、 C、
C、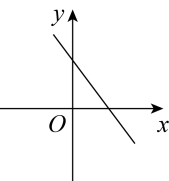 D、
D、 5. 将一副三角板如图1放置,使点A落在DE上,三角板ABC的顶点C与三角板CDE的直角顶点C重合,若 , AB与CE交于点F,则的度数为( )
5. 将一副三角板如图1放置,使点A落在DE上,三角板ABC的顶点C与三角板CDE的直角顶点C重合,若 , AB与CE交于点F,则的度数为( ) A、30° B、45° C、60° D、75°6. 某弹簧的长度y与所挂物体的质量x(kg)之间的关系为一次函数,其函数图象如图所示,则不挂物体时弹簧的长度为( )
A、30° B、45° C、60° D、75°6. 某弹簧的长度y与所挂物体的质量x(kg)之间的关系为一次函数,其函数图象如图所示,则不挂物体时弹簧的长度为( ) A、 B、 C、 D、7. 如图,用10块形状、大小完全相同的小长方形墙砖拼成一个大长方形,设每个小长方形墙砖的长和宽分别为xcm和ycm,则依题意可列方程组为( )
A、 B、 C、 D、7. 如图,用10块形状、大小完全相同的小长方形墙砖拼成一个大长方形,设每个小长方形墙砖的长和宽分别为xcm和ycm,则依题意可列方程组为( ) A、 B、 C、 D、8. 如图,长方形网格中,每个小长方形的长均为2cm,宽均为1cm.△ABC的三个顶点都在长方形网格的格点处,若BD是AC边上的高,则BD的长度为( )cm
A、 B、 C、 D、8. 如图,长方形网格中,每个小长方形的长均为2cm,宽均为1cm.△ABC的三个顶点都在长方形网格的格点处,若BD是AC边上的高,则BD的长度为( )cm A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 如果关于x,y的二元一次方程的一组解是那么m的值为 .10. 甲乙两足球队,他们队员的平均身高都是1.73m,方差分别是、 , 且 , 则两个队队员的身高较整齐的是队(填甲或乙).11. 如图,正比例函数y=﹣2x与一次函数y=ax+b的图象交于点P(﹣1,m),那么二元一次方程组 的解为 .
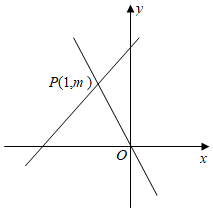 12. 如图,△ABC是等边三角形,边长为2,以边BC所在直线为x轴,以边BC的垂直平分线为y轴建立平面直角坐标系,那么点A的坐标为 .
12. 如图,△ABC是等边三角形,边长为2,以边BC所在直线为x轴,以边BC的垂直平分线为y轴建立平面直角坐标系,那么点A的坐标为 . 13. 若 , , 则代数式的值为 .14. 如图,BE、CF是△ABC的角平分线,BE、CF相交于点D,若 , 则∠CDE的度数为°.
13. 若 , , 则代数式的值为 .14. 如图,BE、CF是△ABC的角平分线,BE、CF相交于点D,若 , 则∠CDE的度数为°.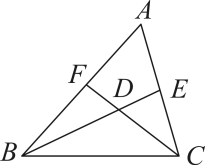 15. 如图,这是一个供滑板爱好者使用的U型池的示意图,该U型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为 的半圆,其边缘 ,点 在 上, ,一滑板爱好者从A点滑到E点,则他滑行的最短距离约为 .(边缘部分的厚度忽略不计)
15. 如图,这是一个供滑板爱好者使用的U型池的示意图,该U型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为 的半圆,其边缘 ,点 在 上, ,一滑板爱好者从A点滑到E点,则他滑行的最短距离约为 .(边缘部分的厚度忽略不计) 16. 甲、乙两人在笔直的公路上从同一起点出发向同一方向匀速步行1200米,先到终点的人原地休息.乙知甲先出发3分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分钟)之间的关系如图所示,下列结论:①甲步行的速度为40米/分;②乙用9分钟追上甲;③整个过程中,有4个时刻甲乙两人相距90米;④乙到达终点时,甲离终点还有280米,其中正确的结论有 . (填写所有正确结论的序号)
16. 甲、乙两人在笔直的公路上从同一起点出发向同一方向匀速步行1200米,先到终点的人原地休息.乙知甲先出发3分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分钟)之间的关系如图所示,下列结论:①甲步行的速度为40米/分;②乙用9分钟追上甲;③整个过程中,有4个时刻甲乙两人相距90米;④乙到达终点时,甲离终点还有280米,其中正确的结论有 . (填写所有正确结论的序号)
三、解答题
-
17. 化简:(1)、;(2)、 .18. 解方程组: .19. 阅读材料:善于思考的小明同学在解方程组时,采用了一种“整体换元”的解法.
解:把 , 看成一个整体,设 , ,
原方程组可化为 ,
解得 , ,
∴原方程组的解为 ,
请仿照小明同学的方法,用“整体换元”法解方程组
20. 某校学生会决定从甲、乙两名学生会干事中选拔一名副主席,选拔包括笔试、面试和民主测评三项,每项得分依次按4:4:2的比例确定个人的最终得分,甲、乙两名候选人的三项成绩如下表所示:测试项目
测试成绩/分
甲
乙
笔试
80
90
面试
70
70
民主测评
80
70
请通过计算说明哪位同学最终得分高?
21. 如图,一艘轮船从A港向南偏西50°方向航行100km到达B岛,再从B岛沿BM方向航行125km到达C岛,A港到航线BM的最短距离是60km(即). (1)、若轮船速度为25km/h,求轮船从C岛沿CA返回A港所需的时间;(2)、请你判断C岛在A港的什么方向 ,并说明理由.22. 如图,直线 , 将Rt△ABC按如图所示的位置放置,点C在直线EF上, , .
(1)、若轮船速度为25km/h,求轮船从C岛沿CA返回A港所需的时间;(2)、请你判断C岛在A港的什么方向 ,并说明理由.22. 如图,直线 , 将Rt△ABC按如图所示的位置放置,点C在直线EF上, , . (1)、若 , 则∠2的度数为多少?(2)、若 , 则∠2的度数为多少?(用含的代数式表示)23. 在“新冠病毒”防控期间,某医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售,两次购进的同一商品进价相同,购进数量和所需费用如表所示:
(1)、若 , 则∠2的度数为多少?(2)、若 , 则∠2的度数为多少?(用含的代数式表示)23. 在“新冠病毒”防控期间,某医疗器械公司分两次购进酒精消毒液与测温枪两种商品进行销售,两次购进的同一商品进价相同,购进数量和所需费用如表所示:项目
购进数量(件)
购进所需费用(元)
酒精消毒液
测温枪
第一次
30
40
8300
第二次
40
30
6400
(1)、求酒精消毒液和测温枪两种商品每件的进价分别是多少元?(2)、公司决定酒精消毒液以每件20元出售,测温枪以每件240元出售.为满足市场需求,需购进这两种商品共1000件.①若设购进测温枪m件,该公司销售完上述1000件商品获得的利润为W元,请写出W与m的函数关系式;
②若购买测温枪数量不超过200件,求该公司销售完上述1000件商品获得的最大利润.
24. 如图,将一个长方形OABC纸片放在平面直角坐标系中,O为原点,点A在x轴正半轴上,点C在y轴正半轴上, , , 将长方形折叠后,点B恰好落在OA边上的点E处,折痕所在直线经过点C且与AB边交于点D,与x轴的正半轴交于点F. (1)、求点D的坐标及直线CD的解析式;(2)、点P是线段CF上的一个动点,若OP将△COF的面积分为1:2两部分,求点P的坐标.
(1)、求点D的坐标及直线CD的解析式;(2)、点P是线段CF上的一个动点,若OP将△COF的面积分为1:2两部分,求点P的坐标.