江西省萍乡市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-11-18 类型:期末考试
一、单选题
-
1. 下列各数是无理数的是( )A、3.414 B、 C、 D、2. 下列语句中,是命题的是( )A、连接A、B两点 B、画一条线段等于已知线段 C、过点M作直线的垂线 D、同旁内角互补,两直线不平行3. 在以下四点中,哪一点与点(-3,4)所连的线段与x轴和y轴都不相交( )A、(-5,1) B、(3,-3) C、(2,2) D、(-2,-1)4. 如图, , 垂足为B, , 则的度数是( )
 A、 B、 C、 D、5. 一个正数的两个平方根分别为与 , 则m的值为( )A、1 B、2 C、 D、6. 直线经过一,三,四,象限,则直线的图象大致是A、
A、 B、 C、 D、5. 一个正数的两个平方根分别为与 , 则m的值为( )A、1 B、2 C、 D、6. 直线经过一,三,四,象限,则直线的图象大致是A、 B、
B、 C、
C、 D、
D、 7. 若关于x,y的方程组的解适合方程 , 则m的值为( )A、 B、1 C、2 D、38. 若一组数据的平均数为17,方差为2,则另一组数据的平均数和方差分别为( )A、17,2 B、17,3 C、18,1 D、18,29. 如图,RtΔABC中,AB=9,BC=6,∠B=90°,将ΔABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( )
7. 若关于x,y的方程组的解适合方程 , 则m的值为( )A、 B、1 C、2 D、38. 若一组数据的平均数为17,方差为2,则另一组数据的平均数和方差分别为( )A、17,2 B、17,3 C、18,1 D、18,29. 如图,RtΔABC中,AB=9,BC=6,∠B=90°,将ΔABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为( ) A、 B、 C、4 D、510. 如图,直线与x轴,y轴分别交于点A和点B,点C在线段上,且点C坐标为 , 点D为线段的中点,点P为上一动点,当的周长最小时,点P的坐标为( )
A、 B、 C、4 D、510. 如图,直线与x轴,y轴分别交于点A和点B,点C在线段上,且点C坐标为 , 点D为线段的中点,点P为上一动点,当的周长最小时,点P的坐标为( )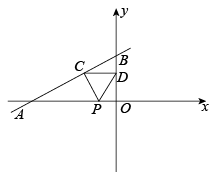 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
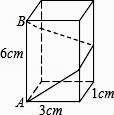
11. 比较大小:(填“>”“<”或“=”).12. 已知平面直角坐标系内两点关于x轴对称,则 .13. 如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要cm.
 14. 已知是关于x的正比例函数,则 .15. 某年级(1)班体育委员对本班50名同学课外延时参加球类自选项目做了统计,制作扇形统计图(如图),则该班选乒乓球人数比选羽毛球人数多人.
14. 已知是关于x的正比例函数,则 .15. 某年级(1)班体育委员对本班50名同学课外延时参加球类自选项目做了统计,制作扇形统计图(如图),则该班选乒乓球人数比选羽毛球人数多人. 16. 把一副直角三角尺按如图所示的方式摆放在一起,其中 , , , ,则 .
16. 把一副直角三角尺按如图所示的方式摆放在一起,其中 , , , ,则 . 17. 如图,在一圆形跑道上,甲从A点、乙从B点同时出发,反向而行,8分后两人相遇,再过6分甲到B点,又过10分两人再次相遇.甲环行一周需分.
17. 如图,在一圆形跑道上,甲从A点、乙从B点同时出发,反向而行,8分后两人相遇,再过6分甲到B点,又过10分两人再次相遇.甲环行一周需分. 18. 如图,在平面直角坐标系中,O为坐标原点,四边形是长方形,点A,C的坐标分别为 , 点D为的中点,点P在边上运动,当时,点P的坐标为 .
18. 如图,在平面直角坐标系中,O为坐标原点,四边形是长方形,点A,C的坐标分别为 , 点D为的中点,点P在边上运动,当时,点P的坐标为 .
三、解答题
-
19.(1)、计算:(2)、若直线和直线的交点坐标为 , 求a,b的值.20. 如图,已知平分 , 求证:平分 .
 21. 如图,在△ABC中,AD,AE分别是BC边上的高和中线,AB=9cm,AC=7cm,BC=8cm,求DE的长.
21. 如图,在△ABC中,AD,AE分别是BC边上的高和中线,AB=9cm,AC=7cm,BC=8cm,求DE的长. 22. 一辆旅游车从大理返回昆明,旅游车距昆明的路程y(千米)与行驶时间x(小时)之间的函数关系如图所示,试回答下列问题:(1)、求此函数的表达式(不必求出自变量的取值范围);(2)、若旅游车8:00从大理出发,11:30在某加油站加油,问此时旅游车距昆明还有多少千米(途中停车时间不计)?
22. 一辆旅游车从大理返回昆明,旅游车距昆明的路程y(千米)与行驶时间x(小时)之间的函数关系如图所示,试回答下列问题:(1)、求此函数的表达式(不必求出自变量的取值范围);(2)、若旅游车8:00从大理出发,11:30在某加油站加油,问此时旅游车距昆明还有多少千米(途中停车时间不计)? 23. 如图,在中,点D为上一点,将沿翻折得到 , 与相交于点F,若平分 , , .
23. 如图,在中,点D为上一点,将沿翻折得到 , 与相交于点F,若平分 , , . (1)、求证:;(2)、求的度数.24. 为创建“绿色校园”,绿化校园环境,某校计划分两次购进A、B两种花草,第一次分别购进A,B两种花草30棵和15棵,共花费675元,第二次分别购进A、B两种花草12棵和5棵,共花费265元(两次购进同种花草和价格相同).求:(1)、A、B两种花草每棵的价格分别是多少元?(2)、若计划购买A、B两种花草共30棵,其中购买A种花草m棵,且 , 请你给出一种费用最省的方案,并求该方案所需费用.25. 在学校组织的“文明出行”知识竞赛中,8(1)和8(2)班参赛人数相同,成绩分为A、B、C三个等级,其中相应等级的得分依次记为A级100分、B级90分、C级80分,达到B级以上(含B级)为优秀,其中8(2)班有2人达到A级,将两个班的成绩整理并绘制成如下的统计图,请解答下列问题:
(1)、求证:;(2)、求的度数.24. 为创建“绿色校园”,绿化校园环境,某校计划分两次购进A、B两种花草,第一次分别购进A,B两种花草30棵和15棵,共花费675元,第二次分别购进A、B两种花草12棵和5棵,共花费265元(两次购进同种花草和价格相同).求:(1)、A、B两种花草每棵的价格分别是多少元?(2)、若计划购买A、B两种花草共30棵,其中购买A种花草m棵,且 , 请你给出一种费用最省的方案,并求该方案所需费用.25. 在学校组织的“文明出行”知识竞赛中,8(1)和8(2)班参赛人数相同,成绩分为A、B、C三个等级,其中相应等级的得分依次记为A级100分、B级90分、C级80分,达到B级以上(含B级)为优秀,其中8(2)班有2人达到A级,将两个班的成绩整理并绘制成如下的统计图,请解答下列问题: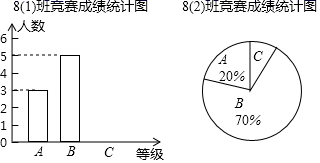 (1)、求各班参赛人数,并补全条形统计图;(2)、此次竞赛中8(2)班成绩为C级的人数为人;(3)、小明同学根据以上信息制作了如下统计表:
(1)、求各班参赛人数,并补全条形统计图;(2)、此次竞赛中8(2)班成绩为C级的人数为人;(3)、小明同学根据以上信息制作了如下统计表:平均数(分)
中位数(分)
方差
8(1)班
m
90
n
8(2)班
91
90
29
请分别求出m和n的值,并从优秀率和稳定性方面比较两个班的成绩;
26. 如图①,直线与x轴、y轴分别交于 , B两点,过点B的另一直线交x轴的负半轴于点C,且 . (1)、求点C的坐标;(2)、求直线的表达式;(3)、直线交于点E,交于点F,交x轴于点D,是否存在这样的直线 , 使?若存在,求出a的值,若不存在,说明理由.
(1)、求点C的坐标;(2)、求直线的表达式;(3)、直线交于点E,交于点F,交x轴于点D,是否存在这样的直线 , 使?若存在,求出a的值,若不存在,说明理由.