江西省景德镇市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-11-18 类型：期末考试

进入出卷网下载

一、单选题

1. 在 $- \sqrt{3}$ ， 0， $\frac{π}{2}$ ， 3.14， $\frac{1}{6}$ ， $\sqrt[3]{4}$ 这些数中，无理数的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
2. 第24届冬季奥林匹克运动会将于2022年2月4日-2022年2月20日在北京市和张家口市联合举行．以下能够准确表示张家口市的地理位置的是（）

A、离北京市200千米 B、东经114.8°，北纬40.8° C、在宁德市北方 D、在河北省西北部

查看试题解析
3. 下列条件中，不能判断 $△ A B C$ 是直角三角形的是（）

A、 $A B ： B C ： A C = 3 ： 4 ： 5$ B、 $A B ： B C ： A C = 1 ： 2 ： \sqrt{3}$ C、 $∠ A - ∠ B = ∠ C$ D、 $∠ A ： ∠ B ： ∠ C = 3 ： 4 ： 5$

查看试题解析
4. 某同学使用计算器求30个数据的平均数时，错将其中的一个数据406输入为46，那么由此求出的平均数与实际平均数的差是（）

A、-12 B、9 C、-9 D、12

查看试题解析
5. 如图，点 $A$ 的坐标为 $(- 1 ， 0)$ ，直线 $y = x - 2$ 与 $x$ 轴交于点 $C$ ，与 $y$ 轴交于点 $D$ ，点 $B$ 在直线 $y = x - 2$ 上运动．当线段 $A B$ 最短时，求点 $B$ 的坐标（）

A、 $(\frac{1}{2} ， - \frac{3}{2})$ B、 $(1 ， - 1)$ C、 $(\frac{1}{3} ， - \frac{5}{3})$ D、 $(0 ， - 2)$

查看试题解析
6. P₁（x₁ ， y₁），P₂（x₂ ， y₂）是平面直角坐标系中的任意两点，我们把|x₁-x₂|+|y₁-y₂|叫做P₁ ， P₂两点间的“直角距离”，记作d（P₁ ， P₂）．比如：点P（2，-4），Q（1，0），则d（P，Q）=|2-1|+|-4-0|=5，已知Q（2，1），动点P（x，y）满足d（P，Q）=3，且x、y均为整数，则满足条件的点P有（）个．

A、4 B、8 C、10 D、12

查看试题解析

二、填空题

7. 比较大小： $- 3$ $- \sqrt{10}$ ．（填“>”，“=”或“<”）

查看试题解析
8. 若正比例函数 $y = k x$ 的图象经过点 $A (k ， 9)$ ，且 $y$ 的值随 $x$ 值的增大而减小，则 $k =$ ．

查看试题解析
9. 某校规定学生的学期数学成绩由平时成绩与期末卷面成绩共同确定，其中平时成绩占40%，期末卷面成绩占60%，小明平时成绩为85分，期末卷面成绩为95分，则小明的学期数学成绩是．

查看试题解析
10. 如图所示，长方形 $A B C D$ ，半圆 $O$ 与直角 $△ E O F$ 分别是学生常用的直尺，量角器与三角板的示意图．已知图中的点 $M$ 处的读数是135°，则 $∠ F N D$ 的度数为．

查看试题解析
11. 已知关于 $x$ ， $y$ 的二元一次方程组 ${\begin{array}{l} 3 x + 2 y + k = 3 \\ 2 x + 3 y + 3 k = 5 \end{array}$ 的解满足 $x + y = - 4$ ，则 $k$ 的值为．

查看试题解析
12. 如图，在长方形 $A B C O$ 中，点 $O$ 为坐标原点，点 $B$ 的坐标为 $(8 ， 6)$ ，点 $A$ ， $C$ 在坐标轴上，直线 $y = 2 x - 6$ 与 $A B$ 交于点 $D$ ，与 $y$ 轴交于点 $E$ ．动点 $P$ 在 $B C$ 边上，点 $Q$ 是坐标平面内的点．当点 $Q$ 在第一象限，且在直线 $y = 2 x - 6$ 上时，若 $△ A P Q$ 是等腰直角三角形，则点 $Q$ 的坐标为．

查看试题解析

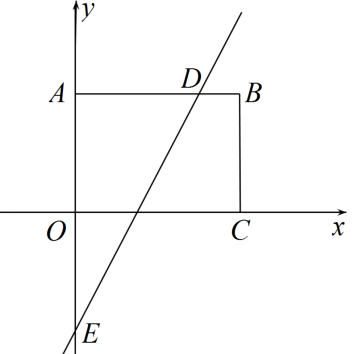
三、解答题

13.

(1)、计算： $(\sqrt{24} - \sqrt{48}) \div \sqrt{3} - 3 \sqrt{\frac{1}{2}}$

(2)、解方程组： ${\begin{array}{l} 3 x - y + z = - 2 \\ 2 x + y - 3 z = - 9 \\ x + y + z = 4 \end{array}$

查看试题解析
14. 甲、乙两人同时解方程组 ${\begin{array}{l} m x + y = 5 ① \\ 2 x - n y = 13 ② \end{array}$ 甲解题看错了①中的 $m$ ，解得 ${\begin{array}{l} x = 2 \\ y = - 3 \end{array}$ ，乙解题时看错②中的 $n$ ，解得 ${\begin{array}{l} x = 3 \\ y = - 7 \end{array}$ ，试求原方程组的解．

查看试题解析
15. 《中华人民共和国道路交通管理条例》规定：小汽车在城街路上行驶速度不得超过 $70 k m / h$ ．如图，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路对面车速检测仪 $A$ 处的正前方 $30 m$ 的 $C$ 处，过了 $2 s$ 后，测得小汽车与车速检测仪间距离为 $50 m$ ，这辆小汽车超速了吗？（参考数据转换： $1 m / s = 3.6 k m / h$ ）

查看试题解析
16. 如图，在 $6 \times 7$ 的正方形的网格图中，点 $A$ ， $B$ ， $C$ 均为格点，仅用无刻度直尺按要求作图．

（ 1 ）在图1中，画一条射线 $A M$ ，使 $∠ B A M = 45 °$ ；

查看试题解析
17. 已知一次函数 $y = (k - 2) x - 3 k + 9$ ．

(1)、 $k$ 为何值时，图象经过原点？

(2)、将该一次函数向上平移5个单位长度后得到的函数图象经过点 $(2 ， 9)$ ，求平移后的函数的解析式．

查看试题解析
18. 某数学兴趣小组研究我国古代《算法统宗》里这样一首诗：我问开店李三公，众客都来到店中，一房七客多七客，一房九客一房空．诗中后两句的意思是：如果每一间客房住7人，那么有7人无房可住；如果每一间客房住9人，那么就空出一间房．

(1)、求该店有客房多少间？房客多少人？

(2)、假设店主李三公将客房进行改造后，房间数大大增加．每间客房收费20钱，且每间客房最多入住4人，一次性订客房18间以上（含18间），房费按8折优惠．若诗中“众客”再次一起入住，他们如何订房更合算？

查看试题解析
19. 若正比例函数 $y_{1} = - x$ 的图象与一次函数 $y_{2} = 2 x + m$ 的图象交于点 $A$ ，且点 $A$ 的横坐标为-2．

(1)、求该一次函数的表达式；

(2)、直接写出方程组 ${\begin{array}{l} x + y = 0 \\ - 2 x + y = m \end{array}$ 的解；

(3)、在一次函数 $y_{2} = 2 x + m$ 的图象上是否存在点 $B$ ，使 $△ A O B$ 的面积为9，若存在，求出点 $B$ 坐标；若不存在，请说明理由．

查看试题解析
20. 我市某中学举办“网络安全知识答题竞赛”，初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛，两个队各选出的5名选手的决赛成绩如图所示．

平均数（分）
中位数（分）
众数（分）
方差（分 $^{2}$ ）
初中部
$a$
8.5
8.5
$s_{初中}^{2}$
高中部
8.5
$b$
$c$
1.6

(1)、根据图示计算出 $a =$ ， $b =$ ， $c =$ ；

(2)、结合两队成绩的平均数和中位数进行分析，哪个队的决赛成绩较好？

(3)、计算初中代表队决赛成绩的方差 $s_{初中}^{2}$ ，并判断哪一个代表队成绩较为稳定．

查看试题解析
21. 同学们以“一块直角三角板和一把直尺”开展数学活动，提出了很多数学问题，请你解答：

(1)、如图1，∠α和∠β具有怎样的数量关系？请说明理由；

(2)、如图2，∠DFC的平分线与∠EGC的平分线相交于点Q，求∠FQG的大小；

(3)、如图3，点P是线段AD上的动点（不与A，D重合），连接PF、PG， $\frac{∠ D F P + ∠ F P G}{∠ E G P}$ 的值是否变化？如果不变，请求出比值；如果变化，请说明理由．

查看试题解析
22. 在初中阶段的函数学习中，我们经历了“确定函数的表达式——利用函数图象研究其性质——运用函数解决问题”的学习过程．在画函数图象时，我们通过描点或平移的方法画出了所学的函数图象．学习了一次函数之后，现在来解决下面的问题：
在y=a|x|+b中，下表是y与x的几组对应值．
x
…
-3
-2
-1
0
1
2
3
…
y
…
8
m
4
2
n
6
8
…

(1)、求这个函数的表达式；

(2)、m ， n=；

(3)、在给出的平面直角坐标系xOy中，描出以上表格中各组对应值为坐标的点，并根据描出的点，画出该函数的图象．根据函数图象可得：
①该函数的最小值为 ▲ ；
②写出该函数的另一条性质；

(4)、已知直线y₁=x+4与函数y=a|x|+b的图象交于两点，则当y₁>y时，x的取值范围为．

查看试题解析
23. 大家在学完勾股定理的证明后发现运用“同一图形的面积用不同方式表示”可以证明一类含有线段的等式，这种解决问题的方法我们称之为等面积法．学有所用：在等腰三角形 $A B C$ 中， $A B = A C$ ，其一腰上的高 $B D = h$ ， $M$ 是底边 $B C$ 上的任意一点， $M$ 到腰 $A B$ 的距离 $M E = h_{1}$ ， $M$ 到腰 $A C$ 的距离 $M F = h_{2}$ ．

(1)、请你结合图形1来证明： $h_{1} + h_{2} = h$ ；

(2)、当点 $M$ 在 $B C$ 延长线上时， $h_{1}$ 、 $h_{2}$ 、 $h$ 之间又有什么样的结论．请你在图2中画出图形，并直接写出结论不必证明；

(3)、请利用以上结论解答下列问题，如图3，在平面直角坐标系中有两条直线 $l_{1} ： y = \frac{3}{4} x + 3$ ， $l_{2} ： y = - 3 x + 3$ ，若 $l_{2}$ 上的一点 $M$ 到 $l_{1}$ 的距离是2，求点 $M$ 的坐标．

查看试题解析

	平均数（分）	中位数（分）	众数（分）	方差（分 $^{2}$ ）
初中部	$a$	8.5	8.5	$s_{初中}^{2}$
高中部	8.5	$b$	$c$	1.6

x	…	-3	-2	-1	0	1	2	3	…
y	…	8	m	4	2	n	6	8	…