江西省吉安市永丰县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-11-18 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，属于无理数的是（　　）

A、﹣2 B、 $\frac{22}{7}$ C、 $\sqrt{3}$ D、0.101001000

查看试题解析
2. 在平面直角坐标系中，点P（2，﹣3）在（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 小明妈妈经营一家皮鞋专卖店，为了提高效益，小明帮妈妈对上个月各种型号的皮鞋销售数量进行了一次统计分析，决定在这个月的进货中多进某种型号皮鞋，此时小明应重点参考（）

A、众数 B、平均数 C、加权平均数 D、中位数

查看试题解析
4. 下列图形中，已知∠1＝∠2，则可得到AB∥CD的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，点A，B，C在一次函数 $y = - 2 x + m$ 的图象上，他们的横坐标依次为－1，1，2．分别过这些点作x轴与y轴的垂线，则图中阴影部分的面积之和是（）

A、1 B、 $\frac{3}{2} (m - 1)$ C、 $3 (m - 1)$ D、3

查看试题解析
6. 某二元方程的解是 ${\begin{array}{l} x = m - 1 \\ y = - 2 m + 1 \end{array}$ （ $m$ 为实数），若把 $x$ 看作平面直角坐标系中点的横坐标， $y$ 看作平面直角坐标系中点的纵坐标，下面说法正确的是（）

A、点 $(x, y)$ 一定不在第一象限 B、点 $(x, y)$ 一定不在第二象限 C、 $y$ 随 $x$ 的增大而增大 D、点 $(x, y)$ 一定不在第三象限

查看试题解析

二、填空题

7. $\sqrt{16}$ 的算术平方根是

查看试题解析
8. 一组数据1，2，3，5，3，4，10的极差是．

查看试题解析
9. 我国南宋著名数学家秦九韶在他的著作《数书九章》一书中，给出了著名的秦九韶公式，也叫三斜求积公式，即如果一个三角形的三边长分别为a，b，c，则该三角形的面积为S= $\sqrt{\frac{1}{4} [a^{2} b^{2} - (\frac{a^{2} + b^{2} - c^{2}}{2})^{2}]}$ ，现已知△ABC的三边长分别为1，2， $\sqrt{5}$ ，则△ABC的面积为．

查看试题解析
10. 如图所示，在长为10m、宽为8m的长方形空地上，沿平行于各边的方向分割出三个全等的小长方形花圃则其中一个小长方形花圃的周长是m.

查看试题解析
11. 直线y＝2x＋b与x轴的交点坐标是(2，0)，则关于x的方程2x＋b＝0的解是．

查看试题解析
12. 已知直线y＝2x﹣2与x轴交于A ，与y轴交于B ，若点C是坐标轴上的一点，且AC＝AB ，则点C的坐标为．

查看试题解析

三、解答题

13.

(1)、解方程组： ${\begin{array}{l} x - y = 8 \\ 3 x + y = 12 \end{array}$ ．

(2)、如图，已知∠1＝75°，∠2＝105°，请证明AB与ED平行？

查看试题解析
14. 已知点 $A (a ， - 3)$ 与点 $B (5 ， b)$ 关于x轴对称，求 $a + b$ 的立方根．

查看试题解析
15. 如图，在3×3的网格中，小正方形的边长为1，连接三个格点得到△ABC ．

(1)、求△ABC的周长．

(2)、BC边上的高是多少？

查看试题解析
16. 已知x﹣2的平方根是±2，2x+y+7的立方根是3，求x²+y²的平方根．

查看试题解析
17. 如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，建立平面直角坐标系后△ABC的顶点均在格点上．

(1)、画出△ABC关于x轴对称的图形△A₁B₁C₁；

(2)、分别写出△A₁B₁C₁的顶点A₁ ， B₁ ， C₁的坐标．

查看试题解析
18. 甲、乙、丙三个家电厂家在广告中都声称，他们的某种电子产品在正常情况下的使用寿命都是8年，质量检测部门对这三家销售的产品的使用寿命进行跟踪调查，统计结果如下：（单位：年）
甲厂：4，5，5，5，5，7，9，12，13，15
乙厂：6，6，8，8，8，9，10，12，14，15
丙厂：4，4，4，6，7，9，13，15，16，16
请回答下列问题

(1)、填写表格．

平均数
众数
中位数
甲厂
8
5
乙厂
9.6
8.5
丙厂
4
8

(2)、这三个厂家的推销广告分别利用了哪一种表示集中趋势的特征数？

(3)、如果你是位顾客，宜选购哪家工厂的产品？为什么？

查看试题解析
19. 如图，已知一次函数y=kx+b的图象经过A(-2，-1)，B(1，3)两点，并且交x轴于点C，交y轴于点D

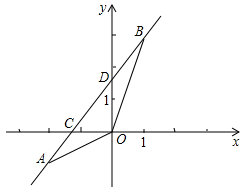(1)、求该一次函数的解析式；

(2)、求△AOB的面积

查看试题解析
20. 某小学在6月1日组织师生共110人到趵突泉公园游览，趵突泉公园规定：成人票价每位40元，学生票价每位20元．该学校购票共花费2400元，在这次游览活动中，教师和学生各有多少人？

查看试题解析
21. 如图，已知 $A B ∥ C D$ ，现将一直角三角形PMN放入图中，其中 $∠ P = 90 °$ ， PM交AB于点E，PN交CD于点F.

(1)、当 $△ P M N$ 在如图1所示的位置时，求出 $∠ P F D$ 与∠AEM的数量关系；

(2)、当 $△ P M N$ 在如图2所示的位置时，求证： $∠ P F D - ∠ A E M = 90 °$ ；

(3)、在（2）的条件下，若MN与CD交于点O，且 $∠ D O N = 20 °$ ， $∠ P E B = 30 °$ ，求 $∠ N$ 的度数．

查看试题解析
22. 阅读下列材料，然后解答下列问题：
在进行代数式化简时，我们有时会碰上如 $\frac{5}{\sqrt{3}}$ ， $\frac{2}{\sqrt{3} + 1}$ 这样的式子，其实我们还可以将其进一步化简：
（一） $\frac{5}{\sqrt{3}} = \frac{5 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{5 \sqrt{3}}{3}$ ；
（二） $\frac{2}{\sqrt{3} + 1} = \frac{2 （ \sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \sqrt{3} - 1$ ；
（三） $\frac{2}{\sqrt{3} + 1} = \frac{3 - 1}{\sqrt{3} + 1} = \frac{(\sqrt{3})^{2} - 1^{2}}{\sqrt{3} + 1} = \frac{(\sqrt{3} + 1) (\sqrt{3} - 1)}{\sqrt{3} + 1} = \sqrt{3} - 1$ ．
以上这种化简的方法叫分母有理化．

(1)、请用不同的方法化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ ：
①参照（二）式化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ ＝．
②参照（三）式化简 $\frac{2}{\sqrt{5} + \sqrt{3}}$ ＝

(2)、化简： $\frac{1}{\sqrt{3} + 1} + \frac{1}{\sqrt{5} + \sqrt{3}} + \frac{1}{\sqrt{7} + \sqrt{5}} + ⋯ + \frac{1}{\sqrt{99} + \sqrt{97}}$ ．

查看试题解析
23. 如图，以Rt△AOC的直角顶点O为原点，以OC、OA所在直线为x轴和y轴建立平面直角坐标系，点A（0，a），C（b，0）满足 $\sqrt{a - 2 b}$ +|b﹣2|＝0．

(1)、C点的坐标为， A点的坐标为；

(2)、如图1，已知坐标轴上有两动点P、Q同时出发，点P从点C出发，沿x轴负方向以1个单位长度每秒的速度匀速移动，点Q从点O出发以2个单位长度每秒的速度沿y轴正方向移动，点Q到达A点整个运动随之结束．AC的中点D的坐标是（1，2），设运动时间为t（t＞0）秒．问：是否存在这样的t，使S_△ODP＝S_△ODQ？若存在，请求出t的值；若不存在，请说明理由；

(3)、如图2，过点O作OG∥AC，作∠AOF＝∠AOG交AC于点F，点E是线段OA上一动点，连接CE交OF于点H，当点E在线段OA上运动的过程中， $\frac{∠ O H C + ∠ A C E}{∠ O E C}$ 的值是否会发生变化？若不变，请求出它的值；若变化，请说明理由，

查看试题解析

	平均数	众数	中位数
甲厂	8	5
乙厂	9.6		8.5
丙厂		4	8