江西省吉安市青原区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-11-18 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中是无理数的是（）

A、 $\sqrt{8}$ B、 $\sqrt[3]{8}$ C、 $π^{0}$ D、 $- \frac{1}{2}$

查看试题解析
2. 下列命题中是假命题的是（）

A、两直线平行，同位角互补 B、对顶角相等 C、直角三角形两锐角互余 D、平行于同一直线的两条直线平行

查看试题解析
3. 下列式子是最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{(a + 1)^{2}}$ C、 $\sqrt{8}$ D、 $\sqrt{a^{2} + 1}$

查看试题解析
4. 如图，有一个水池，水面是一个边长为10尺的正方形，在水池的中央有一根新生的芦苇，它高出水面1尺，如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面，则这个水池的深度是（　　　）尺．

A、26 B、24 C、13 D、12

查看试题解析
5. 《九章算术》是中国古代的一本重要数学著作，其中有一道方程的应用题：“五只雀、六只燕共重16两，雀重燕轻．互换其中一只，恰好一样重．假设每只雀的重量相同，每只燕的重量相同，问每只雀、燕的重量各为多少？”解：设雀每只 $x$ 两，燕每只 $y$ 两，则可列出方程组为（）

A、 ${\begin{array}{l} 6 x + 5 y = 16 \\ 6 x + y = 5 y + x \end{array}$ B、 ${\begin{array}{l} 6 x + 5 y = 16 \\ 5 x + y = 4 y + x \end{array}$ C、 ${\begin{array}{l} 5 x + 6 y = 16 \\ 5 x + y = 6 y + x \end{array}$ D、 ${\begin{array}{l} 5 x + 6 y = 16 \\ 4 x + y = 5 y + x \end{array}$

查看试题解析
6. 当k取不同的值时，y关于x的函数y=kx+2（k≠0）的图象为总是经过点（0，2）的直线，我们把所有这样的直线合起来，称为经过点（0，2）的“直线束”．那么，下面经过点（-1，2）的直线束的函数式是（）

A、y=kx-2（k≠0） B、y=kx+k+2（k≠0） C、y=kx-k+2（k≠0） D、y=kx+k-2（k≠0）

查看试题解析

二、填空题

7. 计算： $2 \sqrt{3} - \sqrt{3} =$

查看试题解析
8. 一个正数的平方根分别是 $x + 1$ 和 $x - 5$ ，则 $x =$ .

查看试题解析
9. 某水果店销售11元，18元，24元三种价格的水果，根据水果店一个月这三种水果销售量的统计图 $($ 如图 $)$ ，可计算出该店当月销售出水果的平均价格是元 $.$

查看试题解析
10. 已知直线 $m ∥ n$ ，将一块含30°角的直角三角板ABC，按如图方式放置（∠ABC=30°），其中A，B两点分别落在直线m，n上，若∠1=18°，则∠2的度数为．

查看试题解析
11. 如图，直线 $l_{1}$ ： $y = x + 2$ 与直线 $l_{2}$ ： $y = k x + b$ 相交于点P（m，4），则方程组 ${\begin{matrix} y = x + 2 \\ y = k x + b \end{matrix}$ 的解是．

查看试题解析
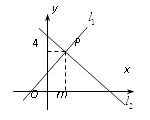12. 已知直线y＝2x﹣2与x轴交于A ，与y轴交于B ，若点C是坐标轴上的一点，且AC＝AB ，则点C的坐标为．

查看试题解析

三、解答题

13.

(1)、计算： $\sqrt{3} × \sqrt{2} - \sqrt{2} + 2 × \sqrt{2}$

(2)、解方程组： ${\begin{array}{l} x - y = 4 ， ① \\ 2 x + y = 5 . ② \end{array}$

查看试题解析
14. 如图是单位长度为1的正方形网格．
（ 1 ）在图1中画出一条长度为 $\sqrt{10}$ 的线段AB；
（ 2 ）在图2中画出一个以格点为顶点，面积为5的正方形．

查看试题解析
15. 二元一次方程组 ${\begin{array}{l} x - 2 y = - 3 \\ 3 x + y = 5 \end{array}$ 的解满足 $2 x - k y = 1$ ，求k的值．

查看试题解析
16. 将一幅三角板拼成如图所示的图形，过点C作CF平分∠DCE交DE于点F，

(1)、求证：CF∥AB，

(2)、求∠DFC的度数.

查看试题解析
17. 已知一次函数的图象经过点（2，1）和（0，-2）．

(1)、求出该函数图象与x轴的交点坐标；

(2)、判断点（-4，6）是否在该函数图象上．

查看试题解析
18. 列二元一次方程组解应用题：某大型超市投入15000元资金购进A、B两种品牌的矿泉水共600箱，矿泉水的成本价和销售价如表所示：
类别/单价
成本价（元/箱）
销售价（元/箱）
A品牌
20
32
B品牌
35
50

(1)、该大型超市购进A、B品牌矿泉水各多少箱？

(2)、全部销售完600箱矿泉水，该超市共获得多少利润？

查看试题解析
19. 如图，在8×8网格纸中，每个小正方形的边长都为1．
（ 1 ）请在网格纸中建立平面直角坐标系，使点A、C的坐标分别为（-4，4），（-1，3），并写出点B的坐标为 ▲ ；
（ 2 ）画出△ABC关于y轴的对称图形△A₁B₁C₁ ，并写出B₁点的坐标；
（ 3 ）在y轴上求作一点P，使△PAB的周长最小，并直接写出点P的坐标

查看试题解析
20. 疫情过后，地摊经济迅速兴起．小李以每千克2元的价格购进某种水果若干千克，销售一部分后，根据市场行情降价销售，销售额 $y$ （元）与销售量 $x$ （千克）之间的关系如图所示．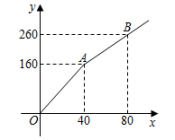

(1)、求降价后销售额 $y$ （元）与销售量 $x$ （千克）之间的函数表达式；

(2)、当销售量为多少千克时，小李销售此种水果的利润为150元？

查看试题解析

21. 为了迎接郑州市第二届“市长杯”青少年校园足球超级联赛，某学校组织了一次体育知识竞赛.每班选25名同学参加比赛，成绩分别为A、B、C、D四个等级，其中相应等级得分依次记为100分、90分、80分、70分.学校将八年级一班和二班的成绩整理并绘制成统计图，如图所示.

(1)、把一班竞赛成绩统计图补充完整；

(2)、写出下表中a、b、c的值：

	平均数（分）	中位数（分）	众数（分）	方差
一班	a	b	90	106.24
二班	87.6	80	c	138.24

(3)、根据（2）的结果，请你对这次竞赛成绩的结果进行分析.

查看试题解析

22. 如图①，在矩形OACB中，点A在x轴正半轴上，点B在y轴正半轴上，点C在第一象限，OA=8，OB=6

(1)、直接写出点C的坐标：；

(2)、如图②，点G在BC边上，连接AG，将△ACG沿AG折叠，点C恰好与线段AB上一点 $C^{'}$ 重合，求线段CG的长度；

(3)、如图③，P是直线y=2x－6上一点，PD⊥PB交线段AC于D．若P在第一象限，且PB=PD，试求符合条件的所有点P的坐标．

查看试题解析
23. 我们新定义一种三角形：若一个三角形中存在两边的平方差等于第三边上高的平方，则称这个三角形为勾股高三角形，两边交点为勾股顶点．

(1)、特例感知：
①等腰直角三角形 ▲ 勾股高三角形（请填写“是”或者“不是”）；
②如图1，已知△ABC为勾股高三角形，其中C为勾股顶点，CD是AB边上的高．若 $B D = 2 A D = 2$ ，试求线段CD的长度．

(2)、深入探究：
如图2，已知△ABC为勾股高三角形，其中C为勾股顶点且CA＞CB，CD是AB边上的高．试探究线段AD与CB的数量关系，并给予证明；

(3)、推广应用：
如图3，等腰△ABC为勾股高三角形，其中 $A B = A C > B C$ ， CD为AB边上的高，过点D向BC边引平行线与AC边交于点E．若 $C E = a$ ，试求线段DE的长度．

查看试题解析

类别/单价	成本价（元/箱）	销售价（元/箱）
A品牌	20	32
B品牌	35	50