江西省吉安市吉安县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-11-18 类型：期末考试

进入出卷网下载

一、单选题

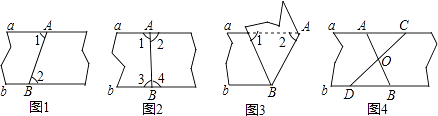
1. 以下四种沿AB折叠的方法中，不一定能判定纸带两条边线a，b互相平行的是（）

A、如图1，展开后测得∠1=∠2 B、如图2，展开后测得∠1=∠2且∠3=∠4 C、如图3，测得∠1=∠2 D、如图4，展开后再沿CD折叠，两条折痕的交点为O，测得OA=OB，OC=OD

查看试题解析
2. 下列各式计算正确的是（）

A、 $\sqrt{6} + \sqrt{2} = \sqrt{8}$ B、 $2 \sqrt{7} + 3 = 5 \sqrt{7}$ C、 $3 \sqrt{2} \times \sqrt{6} = 6 \sqrt{3}$ D、 $\sqrt{20} \div 2 =$ $\sqrt{10}$

查看试题解析
3. 在△ABC中，∠A，∠B，∠C的对边分别记为a，b，c，下列结论中错误的是（）

A、如果a²=b²−c² ，那么△ABC是直角三角形且∠A=90° B、如果∠A：∠B：∠C=1：2：3，那么△ABC是直角三角形 C、如果 $a^{2} ： b^{2} ： c^{2} = 9 ： 16 ： 25$ ，那么△ABC是直角三角形 D、如果 $∠ A - ∠ B = ∠ C$ ，那么△ABC是直角三角形

查看试题解析
4. 化简 $a \sqrt{\frac{1}{- a}}$ 得（）

A、 $\sqrt{a}$ B、 $- \sqrt{a}$ C、 $\sqrt{- a}$ D、 $- \sqrt{- a}$

查看试题解析
5. 如图，AB∥CD，AE平分∠CAB交CD于点E，若∠C=50°，则∠AED为（）

A、130° B、115° C、125° D、120°

查看试题解析
6. 如图是边长为1的4×4的正方形网络，已知A ， B ， C三点均在正方形格点上，则点A到线段BC所在直线的距离是（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、2 D、2.5

查看试题解析

二、填空题

7. $\sqrt{16}$ 的算术平方根是

查看试题解析
8. 点 $P$ 在第四象限内， $P$ 到 $x$ 轴的距离是4，到原点的距离是5，那么点 $P$ 的坐标为．

查看试题解析
9. 中国古代的数学专著《九章算术》有方程组问题“五只雀，六只燕，共重1斤(等于16两)，雀重燕轻．互换其中一只，恰好一样重．”设每只雀、燕的重量各为x两，y两，则根据题意，可得方程组为．

查看试题解析
10. 已知一次函数 $y = a x + | a - 1 |$ 的图象经过点（0，3），且函数y的值随x的增大而减小，则a的值为．

查看试题解析
11. 如图，已知函数y=kx和y=2x+4的图象交于点P，则关于x，y的二元一次方程组 ${\begin{array}{l} y = k x \\ y = 2 x + 4 \end{array}$ 的解是．

查看试题解析
12. 如图，已知格点A的坐标为（1，－2），格点B的坐标为（3，2），在4×4的正方形网格中（小正方形的边长为1）取一格点C，构建三边都为无理数的直角三角形ABC，则格点C的坐标可为．

查看试题解析

三、解答题

13.

(1)、计算： $2 \sqrt{2} (\sqrt{\frac{1}{2}} - \sqrt{6}) + \sqrt{48}$

(2)、解方程组： ${\begin{array}{l} \frac{2 x - y}{5} = 3 \\ \frac{x + y}{3} = 3 \end{array}$

查看试题解析
14. 如图，点 $A$ 所对应的实数为 $a$ ，已知 $O A = O B$ ，请求式子 $| a + \frac{5}{2} | + \sqrt{5} (1 + a)$ 的值．

查看试题解析
15. 下面是两个由边长为1的小正方形组成的 $4 \times 4$ 的正方形网格，小正方形的顶点称为格点．请只用无刻度的直尺在网格（ 1 ）中画一条长为5的线段，在网格（ 2 ）中画一个面积为5的正方形．要求：所画线段的端点和所画正方形的顶点均为格点．

查看试题解析
16. 如图，在△ABC中，已知AB=8，BC=12，AC=18，直线DE是线段AB的垂直平分线，已知线段DE=3．

(1)、求CD的长；

(2)、连接BD，△DBC为何种特殊三角形？并说明理由．

查看试题解析
17. 如图，在平面直角坐标系xOy中，已知点A（0，8），B（6，0），点C（3，a）在线段AB上．

(1)、则a的值为；

(2)、若点D（－4，－3），求直线CD的解析式；

(3)、点（－5，－4）在直线CD上吗？说明理由．

查看试题解析

18. 甲、乙两名射击运动员进行射击比赛，两人在相同条件下，各射击10次，射击的成绩如图所示．根据统计图信息，整理分析数据如下：

	平均成绩（环）	中位数（环）	众数（环）	方差
甲	8	b	8	s²
乙	a	7	c	0.6

(1)、补充表格中a ， b ， c的值，并求甲的方差s²；

(2)、运用表中的四个统计量，简要分析这两名运动员的射击成绩，若选派其中一名参赛，你认为应选哪名运动员？

查看试题解析

19. 某服装店用6000元购进A，B两种新式服装，按标价售出后可获得毛利润3800元（毛利润=售价−进价），这两种服装的进价，标价如表所示．
类型价格
A型
B型
进价（元/件）
60
100
标价（元/件）
100
160

(1)、求这两种服装各购进的件数；

(2)、如果A种服装按标价的8折出售，B种服装按标价的7折出售，那么这批服装全部售完后，服装店比按标价出售少收入多少元?

查看试题解析
20. 李老师一家去离家200千米的某地自驾游，周六上午8点整出发．下面是他们离家的距离y(千米)与汽车行驶时间x(小时)之间的函数图象．

(1)、求他们出发半小时时，离家多少千米？

(2)、出发1小时后，在服务区等另一家人一同前往，等到后以每小时80千米的速度直达目的地；求等侯的时间及线段BC的解析式；

(3)、上午11点时，离目的地还有多少千米？

查看试题解析
21. 阅读下列材料，并解答问题：
① $\frac{1}{\sqrt{2} + \sqrt{4}} = \frac{\sqrt{4} - \sqrt{2}}{2} = \frac{2 - \sqrt{2}}{2}$ ；

② $\frac{1}{\sqrt{4} + \sqrt{6}} = \frac{\sqrt{6} - \sqrt{4}}{2} = \frac{\sqrt{6} - 2}{2}$ ；

③ $\frac{1}{\sqrt{6} + \sqrt{8}} = \frac{\sqrt{8} - \sqrt{6}}{2} = \frac{2 \sqrt{2} - \sqrt{6}}{2}$ ；

④ $\frac{1}{\sqrt{8} + \sqrt{10}} = \frac{\sqrt{10} - \sqrt{8}}{2} = \frac{\sqrt{10} - 2 \sqrt{2}}{2}$ ；……

(1)、直接写出第⑤个等式；

(2)、用含n(n为正整数)的等式表示你探索的规律；

(3)、利用你探索的规律，求 $\frac{1}{\sqrt{2} + \sqrt{4}}$ ＋ $\frac{1}{\sqrt{4} + \sqrt{6}}$ ＋ $\frac{1}{\sqrt{6} + \sqrt{8}}$ ＋…＋ $\frac{1}{\sqrt{198} + \sqrt{200}}$ 的值．

查看试题解析
22. 如图，在△ABC中，∠B=∠C，点D为BC边上(B、C点除外)的动点，∠EDF的两边与AB，AC分别交于点E，F，且BD=CF，BE=DC．

(1)、求证：DE=DF；

(2)、若∠EDF=m°，用含m的代数式表示∠A的度数；

(3)、连接EF，求∠A为多少度数时，△DEF为等边三角形，并说明理由．

查看试题解析
23. 如图1，在平面直角坐标系xOy中，已知点A（0，3），B（2，3），OC=a．将梯形ABCO沿直线y=x折叠，点A落在线段OC上，对应点为E．

(1)、求点E的坐标；

(2)、①若BC $/ /$ AE，求a的值，探究线段BC与AE的数量关系，说明理由．
②如图2，若梯形ABCO的面积为2a，且直线y=mx将此梯形面积分为1∶2的两部分，求直线y=mx的解析式．

查看试题解析

类型价格	A型	B型
进价（元/件）	60	100
标价（元/件）	100	160