江西省赣州市南康区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-11-18 类型：期末考试

进入出卷网下载

一、单选题

1. 下列长度的三条线段，能组成三角形的是（）

A、1，2，5 B、2，2，4 C、2，3，5 D、2，3，4

查看试题解析
2. 下列图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 如图，已知BC＝BD，那么添加下列一个条件后，仍无法判定△ABC≌△ABD的是（）

A、AC＝AD B、∠ABC＝∠ABD C、∠C＝∠D＝90° D、∠CAB＝∠DAB

查看试题解析
4. 下列计算中，正确的是（）

A、 $(x^{3})^{2} = x^{5}$ B、 $x^{3} + x^{2} = x^{5}$ C、 $- x \cdot (- x)^{2} = - x^{3}$ D、 $x^{6} \div x^{2} = x^{3}$

查看试题解析
5. 如图，在△ABC中，∠C＝90°，∠B＝30°，根据尺规作图保留的痕迹，判断下列结论错误的是（）

A、AD是∠BAC的平分线 B、AD=BD C、AD=2CD D、2S_△ABD=3S_△ACD

查看试题解析
6. 课本习题：“A，B两种机器人都被用来搬运化工原料，A型机器人比B型机器人每小时多搬运30kg，A型机器人搬运900kg所用时间与B型机器人搬运600kg所用时间相等，两种机器人每小时分别搬运多少化工原料？”下列四位同学列方程正确的是（）
①设A型机器人每小时搬运xkg化工原料，则：
甲列的方程为： $\frac{900}{x} = \frac{600}{x + 30}$ ；乙列的方程为： $\frac{900}{x} = \frac{600}{x - 30}$
②设A型机器人搬运900kg化工原料需要x小时，则：
丙列的方程为： $\frac{900}{x} + 30 = \frac{600}{x}$ ；丁列的方程为： $\frac{600}{x} + 30 = \frac{900}{x}$

A、甲、丙 B、甲、丁 C、乙、丙 D、乙、丁

查看试题解析

二、填空题

7. 分式 $\frac{2}{x - 1}$ 有意义的条件是．

查看试题解析
8. 因式分解：a³－a=.

查看试题解析
9. 如图，已知△ABC≌△ADE，AD平分∠BAC，∠BAC＝80°，则∠CAE＝°．

查看试题解析
10. 如图，AB//CD，∠1、∠2、∠3是五边形ABCDE的外角，若∠1+∠3＝70°，则∠2＝°．

查看试题解析
11. 如图，已知直线l经过点（0，-1）并且垂直于y轴，若点P（-3，2）与点Q（a，b）关于直线l对称，则a+b＝．

查看试题解析
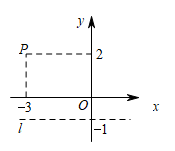12. 如图，在正方形ABCD中，将线段AD绕点A逆时针旋转α°（0＜α＜180）得到线段AE，连接BE、CE．若△EBC是等腰三角形，则α＝．

查看试题解析

三、解答题

13.

(1)、计算： $x (x - y) + 2 x (y - x)$ ．

(2)、如图，C是AB的中点，AD=CE，CD=BE．求证：△ACD≌△CBE．

查看试题解析
14. 解分式方程： $\frac{x - 1}{x - 2} + \frac{1}{x - 2} = 3$ ．

查看试题解析
15. 如图，在平面直角坐标系中，A（-1，2），B（-4，0），C（-3，-2）．

(1)、在图中作出△ABC关于y轴的对称图形△DEF，其中点A与点D对应，点B与点E对称；

(2)、连接CD，CE，则△CDE的面积为．

查看试题解析
16. 先化简，再求值（1- $\frac{3}{x + 1}$ ）÷ $\frac{x^{2} - 4 x + 4}{x + 1}$ ，其中x＝1．

查看试题解析
17. 如图，在△ABC中，AB＝2cm，AC＝4cm．

(1)、尺规作图：作BC边的垂直平分线分别交AC，BC于点D、E（保留作图痕迹，不写作法）；

(2)、在（1）的条件下，连结BD，直接写出△ABD的周长为cm．

查看试题解析
18. 四个全等的长方形（长a，宽b，且a＞b）既可以拼成一个大的长方形（如图1），也可以拼成一个正方形（如图2），通过观察可以发现图2中间空白的部分的面积是 $(a - b)^{2}$ ．

(1)、继续观察，请你直接写出代数式 $(a + b)^{2}$ 、 $(a - b)^{2}$ 、 $a b$ 之间的数量关系；

(2)、根据你得到的关系式解答下列问题：若 $x + y = - 4$ ， $x y = 3$ ，求 $x - y$ 的值．

查看试题解析
19. 如图，AB//CD，∠BAE=∠DCE=45°．判断△ACE的形状，并说明理由．

查看试题解析
20. 如图，在△ABC中，∠BAC＝2∠B，在AB上取AE＝AC，连接CE，作AD⊥CE于点D，交BC于点F．设∠B=α．

(1)、用含α的代数式表示∠AEC为，当∠BCE＝30°时，α＝°；

(2)、判断BC与AD的数量关系，并说明理由．

查看试题解析
21. 一辆汽车开往距离出发地180km的目的地，出发后第一小时内按原计划的速度匀速行驶，一小时后以原来速度的1.5倍匀速行驶，并比原计划提前40min到达目的地．

(1)、原计划的行驶速度是多少？

(2)、这辆汽车实际花费多长时间到达了目的地．

查看试题解析
22. 超市准备购进甲、乙两种绿色袋装食品．甲、乙两种绿色袋装食品的进价和售价如下表．

甲
乙
进价（元/袋）
m
m－2
售价（元/袋）
20
13
已知用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同．

(1)、求m的值；

(2)、要使购进的甲、乙两种绿色袋装食品共800袋，且总利润不少于4800元，则该超市至少购进甲种绿色袋装食品多少袋？

查看试题解析
23. 如图，在△ABC中，AB=AC，分别以AB、AC为腰作等腰直角△ABD、△ACE，两条底边BD、CE交于点F，连接并延长AF交BC于点G．求证：∠FBC=∠FCB，BG＝CG．

查看试题解析
24. 我们知道两个全等的直角三角形（△ABD和△ACE）可以拼成一个等腰三角形（如图1），那么对其中一个直角三角形作适当改变又能得到什么结论呢？现在我们一起来探究吧．

(1)、如图2，将△ACE绕点A逆时针旋转，连接DE，M是DE的中点，连接MB、MC，求证：MB＝MC．

(2)、将CE向上平移，连接DE，M是DE的中点，∠BCM＝30°，连接MB、MC．
①如图3，当∠CAE=∠BAD时，求证：MB＝MC；
②当∠CAE＞∠BAD时，在图4中补全相应的图形，并直接写出MB、MC的数量关系 ▲ ．

查看试题解析

	甲	乙
进价（元/袋）	m	m－2
售价（元/袋）	20	13