江西省赣州市定南县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-11-18 类型：期末考试

进入出卷网下载

一、单选题

1. 某校从认识安全警告标志入手开展安全教育，下列安全图标不是轴对称的是（）

A、 B、 C、 D、

查看试题解析
2. 若分式 $\frac{x - 2}{x + 3}$ 的值为0，则 $x$ 的值等于（）

A、0 B、2 C、3 D、-3

查看试题解析
3. 下列计算结果正确的是（）

A、 $(2 a)^{3} = 6 a^{3}$ B、 $a \div b \cdot \frac{1}{b} = \frac{a}{b^{2}}$ C、 $1 + \frac{1}{a} ＝ \frac{2}{a}$ D、 $(- b c)^{2} \cdot (- b c) = b^{3} c^{3}$

查看试题解析
4. 若一个三角形的两边长分别为3 $cm$ 、6 $cm$ ，则它的第三边的长可能是（）

A、2 $cm$ B、3 $cm$ C、6 $cm$ D、9 $cm$

查看试题解析
5. 图①是一个长为 $2 a$ ，宽为 $2 b$ 的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图②那样拼成一个正方形，则中间空白部分的面积是（）

A、 $a b$ B、 $(a - b)^{2}$ C、 $(2 a + b)^{2}$ D、 $a^{2} - b^{2}$

查看试题解析
6. 如图，在 $△$ ABC中，BA＝BC，∠B＝80°，观察图中尺规作图的痕迹，∠DCE的度数是（）

A、45° B、50° C、55° D、65°

查看试题解析
7. 如图，在等腰 $△ A B C$ 中，BD为 $∠ A B C$ 的平分线， $∠ A = 36 °$ ， AB=AC=a，BC=b，则 $△ A B D$ 的周长为（）

A、 $a + 2 b$ B、 $2 a - b$ C、 $2 a + b$ D、 $a - 2 b$

查看试题解析
8. 如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE=DF，连结BF，CE.下列说法：①△ABD和△ACD面积相等；②∠BAD=∠CAD；③△BDF≌△CDE；④BF∥CE；⑤CE=AE.其中正确的有（）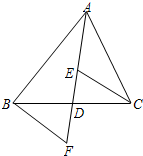

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

9. 分解因式：a²+a= ．

查看试题解析
10. 用科学记数法表示： $0.013697 =$ ．

查看试题解析
11. 已知：如图，AC、BD相交于点O，∠A＝∠D，请你再补充一个条件，使 $△$ AOB≌ $△$ DOC，你补充的条件是．

查看试题解析
12. 若a+b＝3，a²+b²＝7，则ab＝．

查看试题解析
13. 如图，在Rt△ABC中，∠BAC＝90°，∠B＝50°，AD⊥BC ，垂足为D ， △ADB与△ADB'关于直线AD对称，点B的对称点是点B'，则∠CAB'的度数为．

查看试题解析
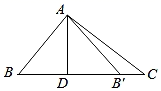14. 如图，在Rt $△$ ABC中，∠B=90°，∠ACB=60°，E是AC的中点，DE⊥AC交AB于D，连接CD．若AD=8，BD的长等于．

查看试题解析
15. 随着快递业务的增加，某快递公司为快递员更换了快捷的交通工具，公司投递快件的能力由每周3000件提高到4200件，平均每人每周比原来多投递80件，若快递公司的快递员人数不变，求原来平均每人每周投递快件多少件？设原来平均每人每周投递快件 $x$ 件，根据题意可列方程为．

查看试题解析
16. 在9×7的正方形网格中，建立如图所示的平面直角坐标系，已知 $△$ ABC三个顶点的坐标分别为A（1，1），B（4，1），C（5，3）．如果要使 $△$ ABD与 $△$ ABC全等，那么符合条件的点D的坐标是．

查看试题解析

三、解答题

17. 计算： ${(- \sqrt{3})}^{0} + 2^{- 2} - | - \frac{1}{4} | + (- 2)^{2}$

查看试题解析
18. 如图，在 $△ A B C$ 中，点D是边BC的中点，连接AD并延长到点E，使DE=AD，连接CE．求证： $△ A B D ≌ △ E C D$

查看试题解析
19. 如图，三角形ABC与三角形DEF关于直线l对称，请仅用无刻度的直尺，在下面两个图中分别作出直线l.

查看试题解析
20. 如图，在△ ABC 中，点 $D 、 E$ 分别在边 $A C 、 A B$ 上， $B D$ 与 $C E$ 交于点O，给出下列三个条件：①∠ $E B O$ =∠ $D C O$ ；② $B E = C D$ ；③ $O B = O C$ .

(1)、上述三个条件中，由哪两个条件可以判定 $Δ A B C$ 是等腰三角形？（用序号写出所有成立的情形）

(2)、请选择（1）中的一种情形，写出证明过程.

查看试题解析
21. 解分式方程： $\frac{x}{x + 1} - 1 = \frac{2 x}{3 x + 3}$

查看试题解析
22. 先化简，再求值 $\frac{1}{a - 1} - \frac{a + 1}{a - 1} \div \frac{a^{2} + 2 a + 1}{a - 1}$ ，在-1，0，1，2四个数中选一个合适的代入求值．

查看试题解析
23. 为了创建全国卫生城市，某社区要清理一个卫生死角内的垃圾，租用甲、乙两车运送，两车各运12趟可完成，需支付运费4800元．已知甲、乙两车单独运完此堆垃圾，乙车所运趟数是甲车的2倍，且乙车每趟运费比甲车少200元．

(1)、求甲、乙两车单独运完此堆垃圾各需运多少趟？

(2)、若单独租用一台车，租用哪台车合算？

查看试题解析
24. 如图1，已知等边 $△$ ABC边长为4cm，点P、Q分别是边AB、BC上的动点，点P、Q分别从点A、B同时出发，且它们的速度都为1cm/s．连接AQ、CP交于点M．

(1)、求证： $△$ ABQ≌ $△$ CAP；

(2)、在整个运动过种中，∠CMQ会发生变化吗？若变化，则说明理由；若不变，求出它的度数．

(3)、连接PQ，何时 $△$ PBQ是直角三角形？

(4)、如图2，若点P、Q在运动到终点后继续在射线AB、BC上运动，直线AQ、CP交于点M，求∠CMQ的度数．

查看试题解析