江西省抚州市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-11-18 类型:期末考试
一、单选题
-
1. 27的立方根为( )A、 B、 C、3 D、92. 在三边分别为4、4、6的等腰三角形中,底边上的高是( )A、5 B、3 C、4 D、3. 在海战中,欲确定敌方每艘战舰的位置,需要知道敌方每艘战舰相对我方潜艇的( )A、距离 B、方位角 C、方位角和距离 D、以上都不对4. 在平面直角坐标系内,一次函数与的图象如图所示,则关于x,y的方程组的解是( )
 A、 B、 C、 D、5. 如图,两条直线和相交于点 , 两直线与x轴所围成的的面积是( )
A、 B、 C、 D、5. 如图,两条直线和相交于点 , 两直线与x轴所围成的的面积是( )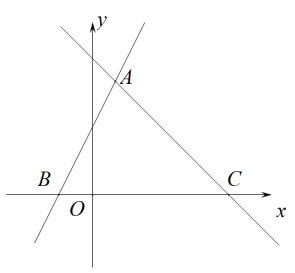 A、 B、 C、75 D、156. 为筹备元旦晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕彩色油纸,如图所示,已知圆筒的高为48cm,其横截面周长为5cm,如果在表面均匀缠绕油纸4圈,应裁剪油纸的长为( )
A、 B、 C、75 D、156. 为筹备元旦晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕彩色油纸,如图所示,已知圆筒的高为48cm,其横截面周长为5cm,如果在表面均匀缠绕油纸4圈,应裁剪油纸的长为( ) A、48cm B、52cm C、60cm D、64cm
A、48cm B、52cm C、60cm D、64cm二、填空题
-
7. 在中, , 则 .8. 我国古代《九章算术》中的“折竹抵地问题”:一根竹子高一丈,折断后竹子顶端落在离竹子底端6尺处,折断处离地面的高度为尺.(一丈=10尺)9. 点与点B关于y轴对称,点B与点C关于x轴对称,则点C的坐标是 .10. 一组数据 , , …,的方差是3,则 , , , …,的方差是 .11. 已知一次函数图象经过与两点,则该函数的图象与y轴交点的坐标为 .12. 直线与平面直角坐标系的x轴、y轴分别交于A,B两点,直线经过B点,且与x轴交于点C,当时是等腰三角形时(举例:直线的解析式为时,就是等腰三角形,此时 , 请写出符合条件的直线的解析式 . (直线除外)
三、解答题
-
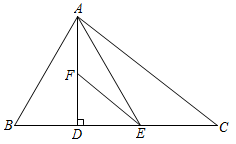
13.(1)、计算:(2)、解方程组:14. 已知 , 且 , 求的平方根.15. 如图,在中, . , 是的高,点E在边上,且是的角平分线,// , 求和的度数.
 16. 如图,在平面直角坐标系中,的各顶点分别为、、
16. 如图,在平面直角坐标系中,的各顶点分别为、、 (1)、在平面直角坐标系中作 , 使与关于y轴对称;(2)、连接 , , 请判定的形状,并说明理由.17. 在平面直角坐标系中,已知两点坐标 , , 若//轴,求一次函数的图像与x轴交点坐标.18. 抚州市“99公益日”关爱困难退役军人募捐活动吸引了大批退役军人及退役军人工作者广泛参与,下列是根据某企业一部门退役军人绘制的捐款人数条形统计图和扇形统计图.
(1)、在平面直角坐标系中作 , 使与关于y轴对称;(2)、连接 , , 请判定的形状,并说明理由.17. 在平面直角坐标系中,已知两点坐标 , , 若//轴,求一次函数的图像与x轴交点坐标.18. 抚州市“99公益日”关爱困难退役军人募捐活动吸引了大批退役军人及退役军人工作者广泛参与,下列是根据某企业一部门退役军人绘制的捐款人数条形统计图和扇形统计图.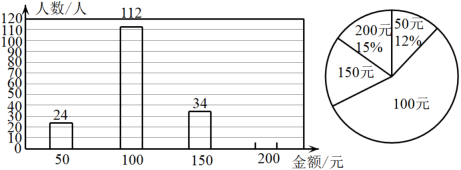 (1)、求该部门总人数,补全条形统计图;(2)、求此次捐款的平均数与中位数;(3)、若该企业有900人,据此样本,请你估计该企业捐款100元的共有多少人?19. 抚州市乡村振兴局在乡村振兴中实施产业振兴,振宇超市积极响应号召,帮助脱贫农户进行葛粉和蜜桔的销售,葛粉售价30元/千克,蜜桔售价20元/千克,第一个月葛粉的销量比蜜桔的销量多1000千克,两种农产品的销售总额达到8万元.(1)、第一个月葛粉和蜜桔的销售量分别为多少千克;(2)、第二个月继续销售这两种农产品,第二个月葛粉售价保持不变,销量比第一个月增加了 . 蜜桔的售价降价四分之一,销量比第一个月增加了 , 结果这两种水果第二个月比上个月的总销售额增加0.4万元,求a的值.20. 根据勾股定理知识迁移,完成下列应用.
(1)、求该部门总人数,补全条形统计图;(2)、求此次捐款的平均数与中位数;(3)、若该企业有900人,据此样本,请你估计该企业捐款100元的共有多少人?19. 抚州市乡村振兴局在乡村振兴中实施产业振兴,振宇超市积极响应号召,帮助脱贫农户进行葛粉和蜜桔的销售,葛粉售价30元/千克,蜜桔售价20元/千克,第一个月葛粉的销量比蜜桔的销量多1000千克,两种农产品的销售总额达到8万元.(1)、第一个月葛粉和蜜桔的销售量分别为多少千克;(2)、第二个月继续销售这两种农产品,第二个月葛粉售价保持不变,销量比第一个月增加了 . 蜜桔的售价降价四分之一,销量比第一个月增加了 , 结果这两种水果第二个月比上个月的总销售额增加0.4万元,求a的值.20. 根据勾股定理知识迁移,完成下列应用. (1)、如图1,分别以直角三角形的三边为直径向外侧作半圆,则它们的面积 , , 之间满足的等量关系是;(2)、应用:如图2,直角三角形的两条直角边长分别为a,b,斜边长为c,分别以三边为直径作半圆,若 , , 求图中阴影部分的面积.21. 如图,已知直线// , , 点E,F在上,且满足 , 平分 .
(1)、如图1,分别以直角三角形的三边为直径向外侧作半圆,则它们的面积 , , 之间满足的等量关系是;(2)、应用:如图2,直角三角形的两条直角边长分别为a,b,斜边长为c,分别以三边为直径作半圆,若 , , 求图中阴影部分的面积.21. 如图,已知直线// , , 点E,F在上,且满足 , 平分 .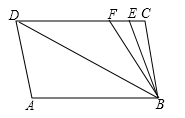 (1)、直线与有何位置关系?请说明理由;(2)、求的度数;(3)、若平行移动 , 在平行移动的过程中是否存在?若存在,求出的度数;若不存在,请说明理由.22. 如图1,已知与都是等腰直角三角形,其中 , 点E为边上一点.
(1)、直线与有何位置关系?请说明理由;(2)、求的度数;(3)、若平行移动 , 在平行移动的过程中是否存在?若存在,求出的度数;若不存在,请说明理由.22. 如图1,已知与都是等腰直角三角形,其中 , 点E为边上一点. (1)、试判断与的大小关系,并说明理由;(2)、求证:;(3)、若E点不在线段上,如图2所示在内,且 , , 求的值.23. 如图,在平面直角坐标系上从原点O出发,有一序列点: , 从开始坐标依次为
(1)、试判断与的大小关系,并说明理由;(2)、求证:;(3)、若E点不在线段上,如图2所示在内,且 , , 求的值.23. 如图,在平面直角坐标系上从原点O出发,有一序列点: , 从开始坐标依次为…
1
4
9
16
…
1
3
6
…
 (1)、请依次写出点 , , 的坐标 , , ;(2)、按规律用含n的代数式写出点的坐标,探讨点 , , , , ......是否在同一直线上,如在同一直线上,请直接写出该直线表达式:如不在同一直线上,请说明理由;(3)、设点的横坐标为m,由点 , , 围成的三角形面积为S,
(1)、请依次写出点 , , 的坐标 , , ;(2)、按规律用含n的代数式写出点的坐标,探讨点 , , , , ......是否在同一直线上,如在同一直线上,请直接写出该直线表达式:如不在同一直线上,请说明理由;(3)、设点的横坐标为m,由点 , , 围成的三角形面积为S,①请补全表1中的空格部分:
②求出S关于m的表达式.