天津市河西区2021-2022学年高二上学期数学期末考试试卷
试卷更新日期:2022-11-17 类型:期末考试
一、单选题
-
1. 观察数列 , (), , ()的特点,则括号中应填入的适当的数为()A、 B、 C、 D、2. 设函数 , 当自变量t由2变到2.5时,函数的平均变化率是( )A、5.25 B、10.5 C、5.5 D、113. 若数列 满足 , ,则该数列的前2021项的乘积是( )A、-2 B、-1 C、2 D、14. 《莱茵德纸草书》是世界上最古老的数学著作之一.书中有这样一道题目:把100个面包分给5个人,使每个人所得成等差数列,且使较大的三份之和的 是较小的两份之和,则最小的一份为( )A、 B、 C、 D、5. 已知函数 的图象如图所示,则其导函数的图象大致形状为( )
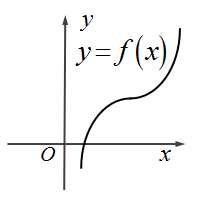 A、
A、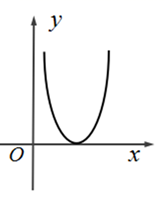 B、
B、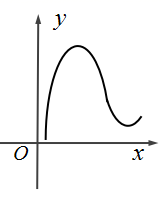 C、
C、 D、
D、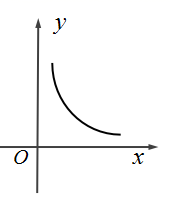 6. 在等差数列中, , 且 , , , 构成等比数列,则公差()A、0或2 B、2 C、0 D、0或7. 函数 的导数为( )A、 B、 C、 D、8. 已知定义在区间 上的函数 , ,若以上两函数的图象有公共点,且在公共点处切线相同,则m的值为( )A、2 B、5 C、1 D、09. 将数列中的各项依次按第一个括号1个数,第二个括号2个数,第三个括号4个数,第四个括号8个数,第五个括号16个数,…,进行排列, , , …,则以下结论中正确的是()A、第10个括号内的第一个数为1025 B、2021在第11个括号内 C、前10个括号内一共有1025个数 D、第10个括号内的数字之和
6. 在等差数列中, , 且 , , , 构成等比数列,则公差()A、0或2 B、2 C、0 D、0或7. 函数 的导数为( )A、 B、 C、 D、8. 已知定义在区间 上的函数 , ,若以上两函数的图象有公共点,且在公共点处切线相同,则m的值为( )A、2 B、5 C、1 D、09. 将数列中的各项依次按第一个括号1个数,第二个括号2个数,第三个括号4个数,第四个括号8个数,第五个括号16个数,…,进行排列, , , …,则以下结论中正确的是()A、第10个括号内的第一个数为1025 B、2021在第11个括号内 C、前10个括号内一共有1025个数 D、第10个括号内的数字之和二、填空题
-
10. 已知数列都是等差数列,公差分别为 , 数列满足 , 则数列的公差为 .11. 已知 , 若三个数成等差数列,则;若三个数成等比数列,则 .12. 函数 , 其导函数为函数 , 则 .13. 已知数列的前n项和为 , 且满足通项公式 , 则 .