山东省枣庄市薛城区2021-2022学年高二上学期理数期末考试试卷
试卷更新日期:2022-11-17 类型:期末考试
一、单选题
-
1. 抛物线的焦点坐标是()A、 B、 C、 D、2. 已知向量 , ,若 ,则 ( )A、-5 B、5 C、4 D、-13. 已知圆的方程为 , 圆的方程为 , 其中 . 那么这两个圆的位置关系不可能为()A、外离 B、外切 C、内含 D、内切4. 如图,把椭圆的长轴分成6等份,过每个分点作x轴的垂线交椭圆的上半部分于点 , F是椭圆C的右焦点,则()
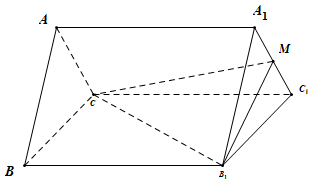
 A、20 B、 C、36 D、305. 在各项都为正数的等比数列 中,首项 ,前3项和为21,则 ( )A、84 B、72 C、33 D、1896. 数学家欧拉1765年在其所著的《三角形几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上,后人称这条直线为欧拉线.已知△ABC的顶点分别为 , , ,则△ABC的欧拉线方程为( )A、 B、 C、 D、7. 已知三棱柱 中, , ,D点是线段 上靠近A的一个三等分点,则 ( )A、 B、 C、 D、8. 已知抛物线 的焦点为 ,准线为l,A是l上一点,B是直线 与抛物线C的一个交点,若 ,则 ( )A、 B、3 C、 D、2
A、20 B、 C、36 D、305. 在各项都为正数的等比数列 中,首项 ,前3项和为21,则 ( )A、84 B、72 C、33 D、1896. 数学家欧拉1765年在其所著的《三角形几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上,后人称这条直线为欧拉线.已知△ABC的顶点分别为 , , ,则△ABC的欧拉线方程为( )A、 B、 C、 D、7. 已知三棱柱 中, , ,D点是线段 上靠近A的一个三等分点,则 ( )A、 B、 C、 D、8. 已知抛物线 的焦点为 ,准线为l,A是l上一点,B是直线 与抛物线C的一个交点,若 ,则 ( )A、 B、3 C、 D、2二、多选题
-
9. 已知曲线C的方程为 , 则()A、曲线C可以表示圆 B、曲线C可以表示焦点在x轴上的椭圆 C、曲线C可以表示焦点在y轴上的椭圆 D、曲线C可以表示焦点在y轴上的双曲线10. 已知数列的前项和为 , , , 数列的前项和为 , , 则下列选项正确的为( )A、数列是等比数列 B、数列是等差数列 C、数列的通项公式为 D、11. 已知直线 上存在相距为4的两个动点A,B,若圆 上存在点P使得 是以点P为直角顶点的等腰直角三角形,则实数a的值可以为( )A、-2 B、-1 C、0 D、112. 在棱长为1的正方体中,点P满足 , , , 则以下说法正确的是()A、当时,直线平面 B、当时,线段CP长度的最小值为 C、当时,直线CP与平面所成的角不可能为 D、当时,存在唯一点P使得直线DP与直线所成的角为
三、填空题
-
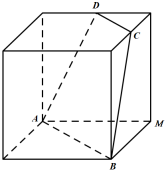
13. 已知空间向量 , , 则向量在向量上的投影向量的坐标是 .14. 数列满足 , 则 .15. 如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是 .
 16. 椭圆 的左、右焦点分别为 , ,过焦点 的直线交该椭圆于 两点,若 的内切圆面积为 , 两点的坐标分别为 , ,则 的面积 , 的值为.
16. 椭圆 的左、右焦点分别为 , ,过焦点 的直线交该椭圆于 两点,若 的内切圆面积为 , 两点的坐标分别为 , ,则 的面积 , 的值为.
四、解答题
-
17.(1)、已知等轴双曲线的上顶点到一条渐近线的距离为 , 求此双曲线的方程;(2)、已知抛物线的焦点为 , 设过焦点且倾斜角为的直线l交抛物线于 , 两点,求线段的长.18. 已知首项为1的等比数列 , 满足 .(1)、求数列的通项公式;(2)、求数列的前n项和 .19. 已知直线 , 圆.(1)、若l与圆C相切,求切点坐标;(2)、若l与圆C交于A,B,且 , 求的面积.20. 在① , ② , ③这三个条件中任选一个,补充在下面问题中,若问题中的存在,求实数的取值范围;若问题中的不存在,请说明理由.
设等差数列的前n项和为 , 数列的前n项和为 , ________, , , 是否存在实数 , 对任意都有?