山东省日照市2020-2021学年高二上学期数学期末校际联合考试试卷

试卷更新日期：2022-11-17 类型：期末考试

进入出卷网下载

一、单选题

1. 直线 $y = \sqrt{3} x + 1$ 的倾斜角是（）

A、 $\frac{π}{3}$ B、 $\frac{π}{4}$ C、 $\frac{3 π}{4}$ D、 $\frac{2 π}{3}$

查看试题解析
2. 抛物线 $x^{2} = - 2 y$ 的焦点到其准线的距离是（）.

A、4 B、2 C、1 D、 $\frac{1}{2}$

查看试题解析
3. 甲、乙两类水果的质量（单位： $k g$ ）分别服从正态分布 $N (μ_{1} ， δ_{1}^{2}) ， N (μ_{2} ， δ_{2}^{2})$ ，其正态分布的密度曲线如图所示，则下列说法错误的是（）

A、甲类水果的平均质量 $μ_{1} = 0.4 k g$ B、甲类水果的质量比乙类水果的质量更集中于平均值左右 C、甲类水果的平均质量比乙类水果的平均质量小 D、乙类水果的质量服从正态分布的参数 $δ_{2} = 1.99$

查看试题解析
4. 如图，在四面体OABC中， $\vec{O A} = \vec{a}$ ， $\vec{O B} = \vec{b}$ ， $\vec{O C} = \vec{c}$ .点M在OA上，且 $O M = 2 M A$ ， $N$ 为BC中点，则 $\vec{M N}$ 等于（）

A、 $\frac{1}{2} \vec{a} - \frac{2}{3} \vec{b} + \frac{1}{2} \vec{c}$ B、 $- \frac{2}{3} \vec{a} + \frac{1}{2} \vec{b} + \frac{1}{2} \vec{c}$ C、 $\frac{1}{2} \vec{a} + \frac{1}{2} \vec{b} - \frac{1}{2} \vec{c}$ D、 $\frac{2}{3} \vec{a} + \frac{2}{3} \vec{b} - \frac{1}{2} \vec{c}$

查看试题解析
5. 已知直线 $l_{1}$ ： $(m + 1) x + 2 y - 1 = 0$ ， $l_{2}$ ： $8 x + (m + 1) y - m + 1 = 0$ ，若 $l_{1} // l_{2}$ ，则 $m =$ （）

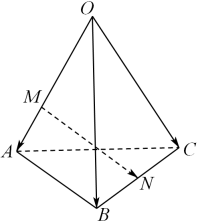A、-1 B、-5 C、-1或3 D、3或-5

查看试题解析
6. 已知椭圆 $\frac{x^{2}}{9} + \frac{y^{2}}{2} = 1$ 的焦点分别为 $F_{1}$ ， $F_{2}$ ，点 $P$ 在椭圆上，若 $| P F_{1} | = 4$ 则三角形 $F_{1} P F_{2}$ 的面积为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\sqrt{3}$ C、 $2 \sqrt{3}$ D、 $4 \sqrt{3}$

查看试题解析
7. 甲、乙、丙、丁四名同学分别从篮球、足球、排球、羽毛球四种球类项目中选择一项进行活动，记事件A为“四名同学所选项目各不相同”，事件B为“只有甲同学选羽毛球”，则 $P (A | B) =$ （）

A、 $\frac{8}{9}$ B、 $\frac{2}{9}$ C、 $\frac{3}{8}$ D、 $\frac{3}{4}$

查看试题解析
8. 双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左右焦点分别为 $F_{1}$ 、 $F_{2}$ ，渐近线为 $l_{1} ， l_{2}$ ，点 $P$ 在第一象限内且在 $l_{1}$ 上，若 $l_{2} ⊥ P F_{1} ， l_{2} ∥ P F_{2} ，$ 则双曲线的离心率为（）

A、 $\sqrt{3}$ B、 $2$ C、 $\sqrt{5}$ D、 $\sqrt{2}$

查看试题解析

二、多选题

9. 已知曲线 $C ： m x^{2} + n y^{2} = 1$ ，下列结论正确的是（）

A、若 $m > n > 0$ ，则 $C$ 是椭圆，其焦点在 $y$ 轴上 B、若 $m > 0 > n$ ，则 $C$ 是双曲线，其焦点在 $x$ 轴上 C、若 $m = n$ ，则 $C$ 是圆 D、若 $m = 0$ ， $n \neq 0$ ，则 $C$ 是两条直线

查看试题解析
10. 某大学为了解学生对学校食堂服务的满意度，随机调查了50名男生和50名女生，每位学生对食堂的服务给出满意或不满意的评价，得到如图所示的列联表.经计算 $K^{2}$ 的观测值 $k \approx 4.762$ ，则可以推断出（）

满意

不满意

男

30

20

女

40

10

$P (K^{2} \geq k)$

0.100

0.050

0.010

$k$

2.706

3.841

6.635

A、该学校男生对食堂服务满意的概率的估计值为 $\frac{3}{5}$ B、调研结果显示，该学校男生比女生对食堂服务更满意 C、有95%的把握认为男、女生对该食堂服务的评价有差异 D、有99%的把握认为男、女生对该食堂服务的评价有差异

查看试题解析
11. 定义：如果在一圆上恰有四个点到一直线的距离等于 $1$ ，那么这条直线叫做这个圆的“相关直线”.则下列直线是圆 $C ： {(x + 1)}^{2} + {(y - 2)}^{2} = 4$ 的“相关直线”的为（）

A、 $y = 1$ B、 $3 x - 4 y + 12 = 0$ C、 $2 x + y = 0$ D、 $12 x - 5 y - 17 = 0$

查看试题解析
12. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，P为线段 $B C_{1}$ 上的动点，下列说法正确的是（）

A、对任意点P ， $D P ∥$ 平面 $A B_{1} D_{1}$ B、点P到平面 $A D D_{1} A_{1}$ 的距离为定值 C、存在点P ，使得直线DP与 $A D_{1}$ 所成的角为 $\frac{π}{4}$ D、存在点P ，使得平面CDP与平面 $A_{1} B_{1} C_{1} D_{1}$ 所成角的大小为 $\frac{π}{3}$

查看试题解析

三、填空题

13. 在 ${(x + \frac{2}{x})}^{5}$ 的二项展开式中， $x^{3}$ 的系数为．

查看试题解析
14. 已知离散型随机变量X的分布列如下表所示，则a＝.

X

1

2

3

P

0.2

a

0.5

查看试题解析
15. 电影《夺冠》讲述了中国女排姑娘们顽强奋斗、为国争光的励志故事，在《夺冠》上映当天，一对夫妇带着他们的两个小孩一起去观看该影片，订购的4张电影票恰好在同一排且连在一起.为安全起见，影院要求每个小孩子要有家长相邻陪坐，则不同的坐法种数是.

查看试题解析
16. 如图，在直三棱柱 $A_{1} B_{1} C_{1} - A B C$ 中， $∠ B A C = \frac{π}{2}$ ， $A B = A C = A_{1} A = 1$ ，已知G与E分别是棱 $A_{1} B_{1}$ 和 $C C_{1}$ 的中点， D与F分别是线段AC与AB上的动点（不包括端点）．若 $G D ⊥ E F$ ，则线段DF的长度的取值范围是．

查看试题解析

四、解答题

17. 在①圆C经过A（4，0），B（6，2），且圆心在直线 $x - y - 6 = 0$ 上；②已知点M（2，0），N（5，0），P（x ， y）为圆C上任一点，P到点M的距离和到点N的距离的比值为2，这两个条件中任选一个条件______，解答下列问题.

(1)、求圆C的标准方程；

(2)、设直线 $y = \sqrt{3} (x - 4)$ 与圆C交于D ， E两点，求弦长 $| D E |$ .

查看试题解析
18. 如图，O为坐标原点，过点P（2，0）且斜率为k的直线l交抛物线 $y^{2} = 2 x$ 于 $M (x_{1} ， y_{1})$ ， $N (x_{2} ， y_{2})$ 两点.

(1)、求 $x_{1} x_{2}$ 的值；

(2)、求证：OM⊥ON.

查看试题解析

19. 共享单车进驻城市，绿色出行引领时尚，某市有统计数据显示，某站点6天的使用单车用户的数据如下，用两种模型①

y = b x + a

；②

y = b \sqrt{x} + a

分别进行拟合，得到相应的回归方程

{\hat{y}}_{1} = 10.7 x + 3.4

，

{\hat{y}}_{2} = 35.5 \sqrt{x} - 22.8

，进行残差分析得到如表所示的残差值及一些统计量的值：

日期x（天）	1	2	3	4	5	6	$\bar{x} = 3.5$ $\bar{y} = 41$ $\sum_{i = 1}^{6} x_{i} y_{i} = 1049$ $\sum_{i = 1}^{6} x_{i}^{2} = 91$
用户y（人）	13	22	43	45	55	68
模型①的残差值	－1.1	－2.8	7.5	－1.2	－1.9	0.4
模型②的残差值	0.3	－5.4	4.3	－3.2	－1.6	3.8

（参考公式： $\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ）

(1)、残差值的绝对值之和越小说明模型拟合效果越好，根据残差，比较模型①，②的拟合效果，应选择哪一个模型？并说明理由；

(2)、残差绝对值大于3的数据认为是异常数据，需要剔除，剔除异常数据后，重新求出（1）中所选模型的回归方程.

查看试题解析

20. 如图，三棱锥P－ABC中， $△ P A B$ 为正三角形，侧面PAB与底面ABC所成的二面角为150°，AB＝AC＝2， $A B ⊥ A C$ ， E ， M ， N分别是线段AB ， PB和BC的中点.

(1)、证明：平面PEN⊥平面ABC；

(2)、求直线PN与平面MAC所成角的正弦值.

查看试题解析

21. 2020年12月4日，“直播带货”入选《咬文嚼字》2020年度十大流行语，与电商直播相关的职业成了年轻人就业新选择.有甲、乙两家农副产品直播间，直播主持人的日工资方案如下：甲直播间底薪100元，直播主持人每箱抽成3元；乙直播间无底薪，80箱以内（含80箱）的部分直播主持人每箱抽成4元，超过80箱的部分直播主持人每箱抽成6元.现从这两家直播间各随机选取一名直播主持人，分别记录其50天的售货箱数，得到如下频数分布表：

售货箱数	60	70	80	90	100
甲直播间天数	5	15	10	15	5
乙直播间天数	5	10	15	12	8

(1)、①从记录甲直播间售货的50天中随机抽取3天，求这3天的售货箱数都不小于80箱的概率；

②以样本估计总体，视样本频率为概率，估计甲直播间主持人3天中至少有2天售货箱数不小于80箱的概率.

(2)、假设同一个直播间的主持人一天的售货箱数相同，将频率视为概率，小张打算到甲、乙两家直播间中的一家应聘主持人，如果从日工资的角度考虑，小张应选择哪家直播间应聘？说明你的理由.

查看试题解析

22. 设圆 $x^{2} + 2 \sqrt{2} x + y^{2} - 14 = 0$ 的圆心为 $A$ ，直线 $l$ 过点 $B (\sqrt{2} ， 0)$ 且与 $x$ 轴不重合， $l$ 交圆 $A$ 于 $C$ 、 $D$ 两点，过 $B$ 作 $A C$ 的平行线交 $A D$ 于点 $E$ ，记点 $E$ 的轨迹为曲线 $Γ$ .

(1)、求曲线 $Γ$ 的方程；

(2)、过坐标原点的直线交曲线 $Γ$ 于 $M$ 、 $N$ 两点，点 $M$ 在第一象限， $M F ⊥ x$ 轴，垂足为 $F$ ，连接 $N F$ 并延长交曲线 $Γ$ 于点 $G$ .证明： $△ M N G$ 是直角三角形.

查看试题解析

	满意	不满意
男	30	20
女	40	10

$P (K^{2} \geq k)$	0.100	0.050	0.010
$k$	2.706	3.841	6.635

X	1	2	3
P	0.2	a	0.5