黑龙江省五校2021-2022学年高二上学期数学期末联考试卷
试卷更新日期:2022-11-17 类型:期末考试
一、单选题
-
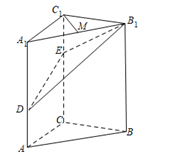
1. 直线的倾斜角为( )A、 B、 C、 D、2. 若两条直线 与 互相垂直,则 的值为( )A、4 B、-4 C、1 D、-13. 已知等差数列 , ,则公差d等于( )A、 B、 C、3 D、-34. 双曲线 的焦点坐标是( )A、 B、 C、 D、5. 双曲线的渐近线方程是()A、 B、 C、 D、6. 已知向量 , , 且与互相平行,则的值为( )A、-2 B、 C、 D、7. 数列 , , , ,……的通项公式可能是()A、 B、 C、 D、8. 如图,在平行六面体 中, ,则与向量 相等的是( )
 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. (多选)下列说法中正确的是()A、若直线的斜率存在,则必有一个倾斜角与之对应 B、每一条直线都有且仅有一个倾斜角与之对应 C、与坐标轴垂直的直线的倾斜角为0°或90° D、若直线的倾斜角为α , 则直线的斜率为tan α10. 如图,在三棱锥中,平面 , , , , 以B为原点,分别以 , , 的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,设平面PAB和平面PBC的一个法向量分别为 , , 则下列结论中正确的是()
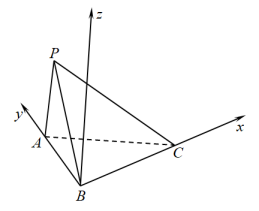 A、点P的坐标为 B、 C、 D、11. 已知数列 , 则下列说法正确的是()A、此数列的通项公式是 B、是它的第23项 C、此数列的通项公式是 D、是它的第25项12. 已知 是椭圆 上一点, , 是其左右焦点,则下列选项中正确的是( )A、椭圆的焦距为2 B、椭圆的离心率 C、 D、 的面积的最大值是4
A、点P的坐标为 B、 C、 D、11. 已知数列 , 则下列说法正确的是()A、此数列的通项公式是 B、是它的第23项 C、此数列的通项公式是 D、是它的第25项12. 已知 是椭圆 上一点, , 是其左右焦点,则下列选项中正确的是( )A、椭圆的焦距为2 B、椭圆的离心率 C、 D、 的面积的最大值是4三、填空题
-
13. 已知P , A , B , C四点共面,对空间任意一点O , 若 , 则.14. 已知圆 , 则圆心坐标为.15. 已知椭圆的左、右焦点分别为 , , 过点的直线与椭圆交于A , B两点,线段AB的长为5,若 , 那么△的周长是.16. 记 为等差数列 的前n项和.若 ,则 .
四、解答题