2023年春季北师版数学九年级下册第二章 《二次函数》单元检测A
试卷更新日期:2022-11-17 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 关于二次函数 ,下列说法正确的是( )A、函数图象的开口向下 B、函数图象的顶点坐标是 C、该函数有最大值,是大值是5 D、当 时,y随x的增大而增大2. 抛物线经平移后,不可能得到的抛物线是( )A、 B、 C、 D、3. 已知点在下列某一函数图象上,且那么这个函数是( )A、 B、 C、 D、4. 若二次函数的图象如图所示,则一次函数与反比例函数在同一坐标系内的大致图象为( )
 A、
A、 B、
B、 C、
C、 D、
D、 5. 已知二次函数的部分函数图象如图所示,则一次函数与反比例函数在同一平面直角坐标系中的图象大致是( )
5. 已知二次函数的部分函数图象如图所示,则一次函数与反比例函数在同一平面直角坐标系中的图象大致是( ) A、
A、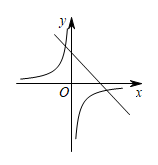 B、
B、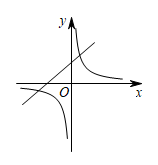 C、
C、 D、
D、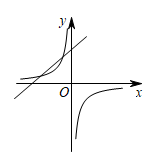 6. 如图是二次函数的图象,其对称轴为直线 , 且过点 . 有以下四个结论:① , ② , ③ , ④若顶点坐标为 , 当时,y有最大值为2、最小值为 , 此时m的取值范围是 . 其中正确结论的个数是( )
6. 如图是二次函数的图象,其对称轴为直线 , 且过点 . 有以下四个结论:① , ② , ③ , ④若顶点坐标为 , 当时,y有最大值为2、最小值为 , 此时m的取值范围是 . 其中正确结论的个数是( )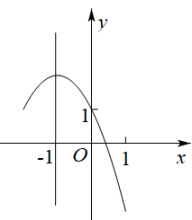 A、4个 B、3个 C、2个 D、1个7. 已知二次函数 , 其中、 , 则该函数的图象可能为( )A、
A、4个 B、3个 C、2个 D、1个7. 已知二次函数 , 其中、 , 则该函数的图象可能为( )A、 B、
B、 C、
C、 D、
D、 8. 点A (m-1,y1),B(m,y2)都在二次函数y=(x-1)2+n的图象上。若y1<y2 , 则m的取值范围为( )A、m>2 B、m> C、m<1 D、 <m<29. 已知点 A(a,2)、B(b,2)、C(c,7)都在抛物线 上,点A在点B左侧,下列选项正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则10. 如图,已知抛物线 的对称轴是 ,直线 轴,且交抛物线于点 ,下列结论错误的是( )
8. 点A (m-1,y1),B(m,y2)都在二次函数y=(x-1)2+n的图象上。若y1<y2 , 则m的取值范围为( )A、m>2 B、m> C、m<1 D、 <m<29. 已知点 A(a,2)、B(b,2)、C(c,7)都在抛物线 上,点A在点B左侧,下列选项正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则10. 如图,已知抛物线 的对称轴是 ,直线 轴,且交抛物线于点 ,下列结论错误的是( )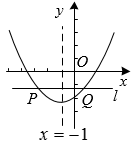 A、 B、若实数 ,则 C、 D、当 时,
A、 B、若实数 ,则 C、 D、当 时,二、填空题(每题3分,共18分)
-
11. 在函数 中,当x>1时,y随x的增大而 .(填“增大”或“减小”)12. 若二次函数的图象上有且只有三个点到x轴的距离等于m,则m的值为 .13. 如图是抛物线形拱桥,当拱顶离水面2米时,水面宽6米,水面下降米,水面宽8米.
 14. 在平面直角坐标系中,将抛物线先绕原点旋转180°,再向下平移5个单位,所得到的抛物线的顶点坐标是.15. 平面直角坐标系 中,已知点 ,且实数m,n满足 ,则点P到原点O的距离的最小值为.16. 如图,二次函数 的函数图象经过点(1,2),且与 轴交点的横坐标分别为 、 ,其中 -1< <0,1< <2,下列结论:① ;② ;③ ;④当 时, ;⑤ ,其中正确的有 .(填写正确的序号)
14. 在平面直角坐标系中,将抛物线先绕原点旋转180°,再向下平移5个单位,所得到的抛物线的顶点坐标是.15. 平面直角坐标系 中,已知点 ,且实数m,n满足 ,则点P到原点O的距离的最小值为.16. 如图,二次函数 的函数图象经过点(1,2),且与 轴交点的横坐标分别为 、 ,其中 -1< <0,1< <2,下列结论:① ;② ;③ ;④当 时, ;⑤ ,其中正确的有 .(填写正确的序号)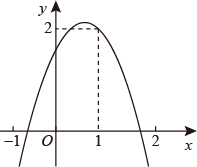
三、解答题(共8题,共72分)
-
17. 某超市购进一批水果,成本为8元/ , 根据市场调研发现,这种水果在未来10天的售价(元/)与时间第天之间满足函数关系式( , 为整数),又通过分析销售情况,发现每天销售量与时间第天之间满足一次函数关系,下表是其中的三组对应值.
时间第天
…
2
5
9
…
销售量
…
33
30
26
…
(1)、求与的函数解析式;(2)、在这10天中,哪一天销售这种水果的利润最大,最大销售利润为多少元?18. 如图,已知二次函数的图象与x轴交于点A,点B,与y轴交于点C,其顶点为D,直线DC的函数解析式为 . 已知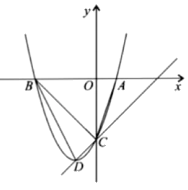 (1)、求二次函数的函数解析式和直线DC的函数解析式;(2)、连接BD,求的面积.19. 北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度为4米,以起跳点正下方跳台底端为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点的坐标为 , 着陆坡顶端与落地点的距离为2.5米,若斜坡的坡度(即).求:
(1)、求二次函数的函数解析式和直线DC的函数解析式;(2)、连接BD,求的面积.19. 北京冬奥会自由式滑雪空中技巧比赛中,某运动员比赛过程的空中剪影近似看作一条抛物线,跳台高度为4米,以起跳点正下方跳台底端为原点,水平方向为横轴,竖直方向为纵轴,建立如图所示平面直角坐标系.已知抛物线最高点的坐标为 , 着陆坡顶端与落地点的距离为2.5米,若斜坡的坡度(即).求: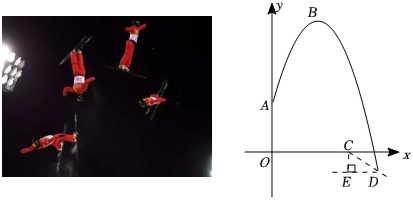 (1)、点的坐标;(2)、该抛物线的函数表达式;(3)、起跳点与着陆坡顶端之间的水平距离的长.(精确到0.1米)(参考数据:)20. 某校为配合疫情防控需要,每星期组织学生进行核酸抽样检测;防疫部门为了解学生错峰进入操场进行核酸检测情况,调查了某天上午学生进入操场的累计人数y(单位:人)与时间x(单位:分钟)的变化情况,发现其变化规律符合函数关系式:数据如下表.
(1)、点的坐标;(2)、该抛物线的函数表达式;(3)、起跳点与着陆坡顶端之间的水平距离的长.(精确到0.1米)(参考数据:)20. 某校为配合疫情防控需要,每星期组织学生进行核酸抽样检测;防疫部门为了解学生错峰进入操场进行核酸检测情况,调查了某天上午学生进入操场的累计人数y(单位:人)与时间x(单位:分钟)的变化情况,发现其变化规律符合函数关系式:数据如下表.时间x(分钟)
0
1
2
3
…
8
累计人数y(人)
0
150
280
390
…
640
640
(1)、求a,b,c的值;(2)、如果学生一进入操场就开始排队进行核酸检测,检测点有4个,每个检测点每分钟检测5人,求排队人数的最大值(排队人数-累计人数-已检测人数);(3)、在(2)的条件下,全部学生都完成核酸检测需要多少时间?如果要在不超过20分钟让全部学生完成核酸检测,从一开始就应该至少增加几个检测点?21. 如图,抛物线经过点和点 , 与轴的另一个交点为 , 连接、 .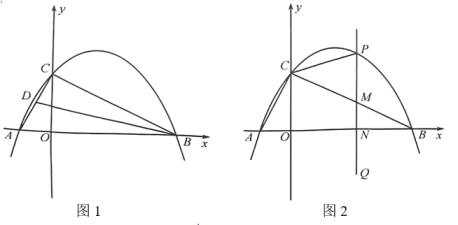 (1)、求抛物线的解析式及点的坐标;(2)、如图1,若点是线段的中点,连接 , 在轴上是否存在点 , 使得是以为斜边的直角三角形?若存在,请求出点的坐标;若不存在,请说明理由;(3)、如图2,点是第一象限内抛物线上的动点,过点作轴,分别交、轴于点、 , 当中有某个角的度数等于度数的2倍时,请求出满足条件的点的横坐标.22. 如图,抛物线y=ax2+bx+c交x轴于A(-1,0),B两点,交y轴于点C(0,3),顶点D的横坐标为1.
(1)、求抛物线的解析式及点的坐标;(2)、如图1,若点是线段的中点,连接 , 在轴上是否存在点 , 使得是以为斜边的直角三角形?若存在,请求出点的坐标;若不存在,请说明理由;(3)、如图2,点是第一象限内抛物线上的动点,过点作轴,分别交、轴于点、 , 当中有某个角的度数等于度数的2倍时,请求出满足条件的点的横坐标.22. 如图,抛物线y=ax2+bx+c交x轴于A(-1,0),B两点,交y轴于点C(0,3),顶点D的横坐标为1.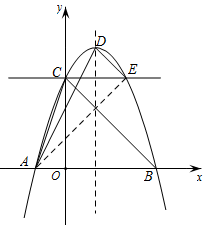 (1)、求抛物线的解析式;(2)、在y轴的负半轴上是否存在点P使∠APB+∠ACB=180°.若存在,求出点P的坐标,若不存在,请说明理由;(3)、过点C作直线l与y轴垂直,与抛物线的另一个交点为E,连接AD,AE,DE,在直线l下方的抛物线上是否存在一点M,过点M作MF⊥l,垂足为F,使以M,F,E三点为顶点的三角形与ΔADE相似?若存在,请求出M点的坐标,若不存在,请说明理由.23. 已知抛物线 与x轴相交于点 , ,与y轴相交于点C.
(1)、求抛物线的解析式;(2)、在y轴的负半轴上是否存在点P使∠APB+∠ACB=180°.若存在,求出点P的坐标,若不存在,请说明理由;(3)、过点C作直线l与y轴垂直,与抛物线的另一个交点为E,连接AD,AE,DE,在直线l下方的抛物线上是否存在一点M,过点M作MF⊥l,垂足为F,使以M,F,E三点为顶点的三角形与ΔADE相似?若存在,请求出M点的坐标,若不存在,请说明理由.23. 已知抛物线 与x轴相交于点 , ,与y轴相交于点C.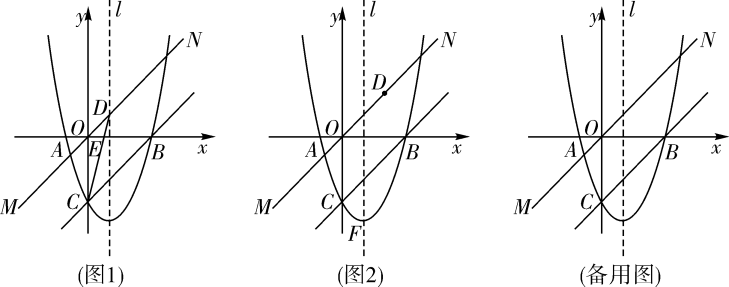 (1)、求抛物线的表达式;(2)、如图1,将直线BC间上平移,得到过原点O的直线MN.点D是直线MN上任意一点.
(1)、求抛物线的表达式;(2)、如图1,将直线BC间上平移,得到过原点O的直线MN.点D是直线MN上任意一点.①当点D在抛物线的对称轴l上时,连接CD,关x轴相交于点E,求线段OE的长;
②如图2,在抛物线的对称轴l上是否存在点F,使得以B,C,D,F为顶点的四边形是平行四边形?若存在,求出点F与点D的坐标;若不存在,请说明理由.
24. 如图,已知抛物线: 与x轴交于点A, (A在B的左侧),与y轴交于点C,对称轴是直线 ,P是第一象限内抛物线上的任一点.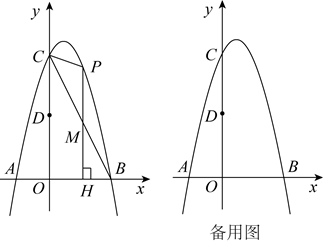 (1)、求抛物线的解析式;(2)、若点D为线段 的中点,则 能否是等边三角形?请说明理由;(3)、过点P作x轴的垂线与线段 交于点M,垂足为点H,若以P,M,C为顶点的三角形与 相似,求点P的坐标.
(1)、求抛物线的解析式;(2)、若点D为线段 的中点,则 能否是等边三角形?请说明理由;(3)、过点P作x轴的垂线与线段 交于点M,垂足为点H,若以P,M,C为顶点的三角形与 相似,求点P的坐标.