四川省雅安市2023届高三理数零诊考试试卷

试卷更新日期：2022-11-16 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知全集 $U = R$ ，集合 $M = {x | x^{2} > 4}$ ， $N = {x | - 1 < x < 3}$ ．则 $(∁_{U} M) \cap N =$ （）

A、 ${x | - 1 < x \leq 1}$ B、 ${x | - 1 \leq x \leq 1}$ C、 ${x | - 1 < x \leq 2}$ D、 ${x | - 1 \leq x \leq 2}$

查看试题解析
2. 已知复数z满足 $(2 + i) z = 2 - 4 i$ ，则 ${(\bar{z} - 2)}^{2} =$ （）

A、 $- 8 i$ B、 $8 i$ C、 $8 - 8 i$ D、 $8 + 8 i$

查看试题解析
3. 某地区今年夏天迎来近50年来罕见的高温极端天气，当地气象部门统计了八月份每天的最高气温和最低气温，得到如下图表：
某地区2022年8月份每天最高气温与最低气温

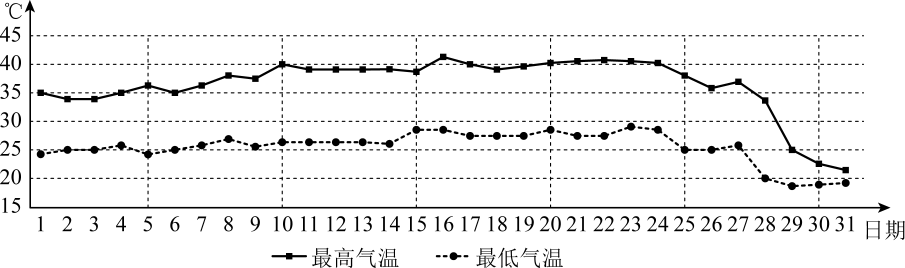
根据图表判断，以下结论正确的是（）

A、8月每天最高气温的平均数低于35℃ B、8月每天最高气温的中位数高于40℃ C、8月前半月每天最高气温的方差大于后半月最高气温的方差 D、8月每天最高气温的方差大于每天最低气温的方差

查看试题解析
4. 若 $\sin (\frac{π}{4} - α) = \frac{2}{3}$ ，则 $\sin 2 α =$ （）

A、 $\frac{1}{9}$ B、 $\frac{4}{9}$ C、 $\frac{5}{9}$ D、 $\frac{8}{9}$

查看试题解析
5. 函数 $f (x) = \frac{e^{x} + e^{- x}}{4} \cdot \sin (2 x - \frac{3 π}{2})$ 在 $[- 4 ， 4]$ 上的图象大致是（）

A、 B、 C、 D、

查看试题解析
6. 执行如图所示的程序框图，输出S的值为（）

A、20 B、40 C、70 D、112

查看试题解析
7. 中国古代数学名著《九章算术》中“均输”一章有如下问题：“今有竹九节，下三节容量四升，上四节容量三升．问中间二节欲均容各多少．”意思是“今有竹9节，下部分3节总容量4升，上部分4节总容量3升，且自下而上每节容积成等差数列，问中间二节容积各是多少？”按此规律，中间二节（自下而上第四节和第五节）容积之和为（）

A、 $\frac{47}{22}$ B、 $\frac{131}{66}$ C、 $\frac{127}{66}$ D、 $\frac{113}{66}$

查看试题解析
8. 甲、乙、丙、丁4名志愿者参加新冠疫情防控志愿者活动，现有A ， B ， C三个小区可供选择，每个志愿者只能选其中一个小区去服务．则甲不在A小区、乙不在B小区服务的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{4}{9}$ C、 $\frac{5}{9}$ D、 $\frac{7}{12}$

查看试题解析
9. 如图，在等腰直角 $△ A B C$ 中，斜边 $B C = 4$ ， $M ， N$ 为线段BC上的动点，且 $M N = 1$ ，则 $\vec{A M} \cdot \vec{A N}$ 的最小值为（）

A、 $\frac{13}{4}$ B、 $\frac{15}{4}$ C、4 D、6

查看试题解析
10. 已知下面给出的四个图都是各棱长均相等的直三棱柱，A为一个顶点，D ， F ， F分别是所在棱的中点．则满足直线 $A D ⊥ E F$ 的图形个数是（）

A、1 B、2 C、3 D、4

查看试题解析
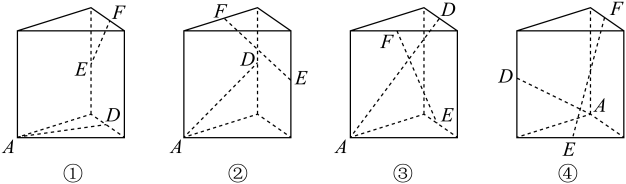11. 已知函数 $f (x) = \sin (ω x + \frac{π}{6}) (ω > 0)$ ．给出以下几个结论：
①若对任意 $x \in R$ ，均有 $f (x) = f (\frac{π}{3} - x)$ ，则 $ω$ 的最小值为2；

②若对任意 $x \in R$ ，均有 $f (x) = - f (\frac{π}{3} - x)$ ，则 $ω$ 的最小值为5；

③若 $f (x)$ 在区间 $(0 ， \frac{π}{2})$ 上的极小值点有且仅有2个，则 $\frac{20}{3} < ω \leq \frac{32}{3}$ ．

其中，正确结论的序号是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析
12. 设 $a = \frac{1}{6 \sqrt{15}}$ ， $b = \frac{3}{4} \sin \frac{1}{60}$ ， $c = \ln \frac{61}{60}$ ，则a ， b ， c的大小关系正确的是（）

A、 $c<a<b$ B、 $c < b < a$ C、 $b<c<a$ D、 $b < a < c$

查看试题解析

二、填空题

13. 在 ${(2 x - a)}^{6}$ 的展开式中， $x^{3}$ 的系数为 $- 20$ ，则 $a =$ ．

查看试题解析
14. 给出两个条件：① $a ， b \in R$ ， $f (a + b) = f (a) f (b)$ ；②当 $x \in (0 ， + \infty)$ 时， $f^{'} (x) < 0$ （其中 $f^{'} (x)$ 为 $f (x)$ 的导函数）．请写出同时满足以上两个条件的一个函数．（写出一个满足条件的函数即可）

查看试题解析
15. 已知数列 ${a_{n}}$ 满足 $a_{1} a_{2} a_{3} \dots a_{n} = 2^{n^{2}}$ ．若对任意 $n \in N^{*}$ ， $\frac{1}{a_{1}} + \frac{1}{a_{2}} + \dots + \frac{1}{a_{n}} < \log_{m} \sqrt[3]{4}$ （ $m > 0$ 且 $m \neq 1$ ）恒成立，则m的取值范围为．

查看试题解析
16. 如图所示的三棱锥 $A - B C D$ 中， $△ B C D$ 为等腰直角三角形，且 $B C = B D = 2 \sqrt{2}$ ，侧棱 $A B = 2$ ， $\cos ∠ A B C = \cos ∠ A B D = - \frac{\sqrt{2}}{4}$ ，则经过该三棱锥四个顶点的球的表面积为．

查看试题解析

三、解答题

17. 某地区对高一年级学生进行体质健康测试（简称体测），现随机抽取了900名学生的体测结果等级（“良好及以下”或“优秀”）进行分析．得到如下列联表：

	良好及以下	优秀	合计
男	450	200	650
女	150	100	250
合计	600	300	900

附表及公式：

$P (K^{2} \geq k_{0})$	0.15	0.10	0.05	0.025	0.010	0.005	0.001
$k_{0}$	2.072	2.706	3.841	5.024	6.635	7.879	10.828

其中 $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ， $n = a + b + c + d$ ．

(1)、计算并判断是否有99％的把握认为本次体测结果等级与性别有关系？

(2)、将频率视为概率，用样本估计总体．若从该地区高一所有学生中，采取随机抽样的方法每次抽取1名学生成绩进行具体指标分析，连续抽取3次，且各次抽取的结果相互独立，记被抽取到的3名学生的体测等级为“优秀”的人数为

ξ

，求

ξ

的分布列和数学期望

E (ξ)

．

查看试题解析

18. 记 $△ A B C$ 的内角A ， B ， C的对边分别为a ， b ， c ，已知 $\frac{2 a \cos A}{c} = \cos B + \frac{\sin B}{\tan C}$ ．

(1)、求角A的大小；

(2)、若点D在边BC上， $A D = 3$ ，且 $B D = 3 D C$ ，求 $△ A B C$ 面积的最大值．

查看试题解析
19. 如图①， $△ A B C$ 为边长为6的等边三角形，E ， F分别为AB ， AC上靠近A的三等分点，现将 $△ A E F$ 沿EF折起，使点A翻折至点P的位置，且二面角 $P - E F - C$ 的大小为120°（如图②）．

(1)、在PC上是否存在点H ，使得直线 $F H / /$ 平面PBE？若存在，确定点H的位置；若不存在，说明理由．

(2)、求直线PC与平面PBE所成角的正弦值．

查看试题解析
20. 给出以下条件：① $a_{2}$ ， $a_{3} + 2$ ， $a_{6} + 4$ 成等比数列；② $S_{2}$ ， $a_{6}$ ， $S_{4} + 4$ 成等比数列；③ $\frac{1}{a_{5}}$ 是 $\frac{1}{S_{2}}$ 与 $\frac{1}{S_{5}}$ 的等差中项．从中任选一个，补充在下面的横线上，再解答．
已知单调递增的等差数列 ${a_{n}}$ 的前n项和为 $S_{n}$ ，且 $a_{1} = 2$ ， ______．

注：如果选择多个条件分别解答，按第一个解答计分．

(1)、求 ${a_{n}}$ 的通项公式；

(2)、令 ${\frac{b_{n}}{a_{n}}}$ 是以2为首项，2为公比的等比数列，数列 ${b_{n}}$ 的前n项和为 $T_{n}$ ．若 $n \in N^{*}$ ， $λ (T_{n} + 2^{n + 2} - 4) \geq 8 S_{n} - 26 a_{n}$ ，求实数 $λ$ 的取值范围．

查看试题解析
21. 已知函数 $f (x) = \frac{x + 3}{e^{x}} - a x^{2} + 2 x - 3$ ．

(1)、当 $a = - \frac{1}{2}$ 时，函数 $y = f (x) - m$ 有三个零点，求m取值范围；

(2)、若 $f (x) \leq 0$ ，求a的取值范围．

查看试题解析
22. 数学中有许多美丽的曲线，如在平面直角坐标系xOy中，曲线 $E ： x^{2} + y^{2} = a (\sqrt{x^{2} + y^{2}} - y) (a > 0)$ 的形状如心形（如图），称这类曲线为心形曲线．以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系．当 $a = 2$ 时，

(1)、求E的极坐标方程；

(2)、已知P ， Q为曲线E上异于O的两点，且 $\vec{O P} \cdot \vec{O Q} = 0$ ，求 $△ O P Q$ 的面积的最大值．

查看试题解析
23. 已知 $a > 0$ ， $b > 0$ ，且 $a + b = 4$ ，证明：

(1)、 $3 a^{2} + b^{2} \geq 12$ ；

(2)、 $\frac{1}{a + 1} + \frac{4}{b} \geq \frac{9}{5}$ ．

查看试题解析