广西普通高中2023届高三理数摸底测试试卷
试卷更新日期:2022-11-16 类型:高考模拟
一、单选题
-
1. 已知集合 ,集合 ,则 ( )A、 B、 C、 D、2. 沙糖桔网店2019年全年的月收支数据如图所示,则针对2019年这一年的收支情况,下列说法中错误的是()
 A、月收入的最大值为90万元,最小值为30万元 B、这一年的总利润超过400万元 C、这12个月利润的中位数与众数均为30 D、7月份的利润最大3. 已知复数(其中为虚数单位),则()A、1 B、 C、 D、4. “”是“方程表示椭圆”的()A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分也不必要条件5. 若将函数的图象向右平移个单位后,所得图象对应的函数为奇函数,则的最小值是( )A、 B、 C、 D、6. 将3个1和4个0随机排成一行,则3个1任意两个1都不相邻的概率为()A、 B、 C、 D、7. 已知 , 则( )A、 B、 C、 D、8. 已知函数存在最大值0,则的值为()A、 B、 C、1 D、9. 生物体死亡后,它机体内原有的碳14含量C会按确定的比率衰减(称为衰减率),C与死亡年数t之间的函数关系式为(k为常数),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.若2022年某遗址文物出土时碳14的残余量约为原始量的85%,则可推断该文物属于()
A、月收入的最大值为90万元,最小值为30万元 B、这一年的总利润超过400万元 C、这12个月利润的中位数与众数均为30 D、7月份的利润最大3. 已知复数(其中为虚数单位),则()A、1 B、 C、 D、4. “”是“方程表示椭圆”的()A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分也不必要条件5. 若将函数的图象向右平移个单位后,所得图象对应的函数为奇函数,则的最小值是( )A、 B、 C、 D、6. 将3个1和4个0随机排成一行,则3个1任意两个1都不相邻的概率为()A、 B、 C、 D、7. 已知 , 则( )A、 B、 C、 D、8. 已知函数存在最大值0,则的值为()A、 B、 C、1 D、9. 生物体死亡后,它机体内原有的碳14含量C会按确定的比率衰减(称为衰减率),C与死亡年数t之间的函数关系式为(k为常数),大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.若2022年某遗址文物出土时碳14的残余量约为原始量的85%,则可推断该文物属于()参考数据:;参考时间轴:
 A、战国 B、汉 C、唐 D、宋10. 设球与圆锥的体积分别为 , , 若球的表面积与圆锥的侧面积相等,且圆锥的轴截面为正三角形,则的值是()A、 B、 C、 D、11. 满足不等式的整数解的个数为()A、 B、 C、 D、12. 已知 , 则的大小关系为()A、 B、 C、 D、
A、战国 B、汉 C、唐 D、宋10. 设球与圆锥的体积分别为 , , 若球的表面积与圆锥的侧面积相等,且圆锥的轴截面为正三角形,则的值是()A、 B、 C、 D、11. 满足不等式的整数解的个数为()A、 B、 C、 D、12. 已知 , 则的大小关系为()A、 B、 C、 D、二、填空题
-
13. 已知向量 , , 若与垂直,则.14. 直线与圆:相交于 , 两点,则.15. 如图所示,已知双曲线:的右焦点为 , 双曲线的右支上一点 , 它关于原点的对称点为 , 满足 , 且 , 则双曲线的离心率是.
 16. 已知在中,角 , , 的对边分别为 , , , , 是的中点,若 , 则的最大值为.
16. 已知在中,角 , , 的对边分别为 , , , , 是的中点,若 , 则的最大值为.三、解答题
-
17. 某学校共有1000名学生参加数学知识竞赛,其中男生200人.为了了解该校学生在数学知识竞赛中的情况,采取按性别分层抽样,随机抽取了100名学生进行调查,分数分布在450~950分之间.将分数不低于750分的学生称为“高分选手”.根据调查的结果绘制的学生分数频率分布直方图如图所示.

参考公式: , 其中.
0.15
0.10
0.05
0.025
0.010
0.005
0.001
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)、求的值,并估计该校学生分数的平均数(同一组中的数据用该组区间的中点值作代表);(2)、若样本中属于“高分选手”的男生有10人,完成下列列联表,并判断是否有99.5%的把握认为该校学生属于“高分选手”与“性别”有关.属于“高分选手”
不属于“高分选手”
合计
男生
女生
合计
18. 设数列的前项和为 , 且满足(1)、求数列的通项公式;(2)、设数列满足 , 求数列的前项和.19. 如图,多面体中,是菱形, , 平面 , , 且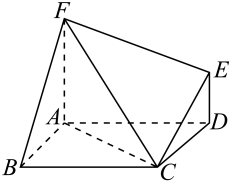 (1)、求证:平面平面;(2)、求二面角的正弦值.20. 如图,已知点是焦点为的抛物线:上一点, , 是抛物线上异于的两点,且直线 , 的倾斜角互补,若直线的斜率为.
(1)、求证:平面平面;(2)、求二面角的正弦值.20. 如图,已知点是焦点为的抛物线:上一点, , 是抛物线上异于的两点,且直线 , 的倾斜角互补,若直线的斜率为. (1)、证明:直线的斜率为定值;(2)、在中,记 , , 求最大值.
(1)、证明:直线的斜率为定值;(2)、在中,记 , , 求最大值.