浙江省台州市仙居县、三门县2021-2022学年八年级上学期期末联考数学试题

试卷更新日期：2022-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列长度的三条线段中，能组成三角形的是（）

A、3，6，10 B、2，2，4 C、3，4，7 D、6，7，8

查看试题解析
3. 下列运算中，正确的是（）

A、 $x^{2} + x^{2} = x^{4}$ B、 $3 x^{2} \cdot 4 x = 12 x^{3}$ C、 $x^{6} \div x^{2} = x^{3}$ D、 ${(- x^{3} y)}^{2} = - x^{6} y^{2}$

查看试题解析
4. 下列各式中与分式 $\frac{- n}{m - n}$ 相等的是（）

A、 $- \frac{n}{n - m}$ B、 $\frac{n}{n - m}$ C、 $\frac{- n}{n - m}$ D、 $- \frac{n}{n + m}$

查看试题解析
5. 一个多边形每一个外角都等于20°，则这个多边形的边数为（）

A、12 B、14 C、16 D、18

查看试题解析
6. 如图，已知 $A B = A D ， A E = A C = B C ， ∠ 1 = ∠ 2 ， ∠ C = 40 °$ ，则 $∠ A D E$ 的度数为（）

A、 $40 °$ B、 $65 °$ C、 $70 °$ D、 $75 °$

查看试题解析
7. 如图，在边长为a的正方形中挖掉一个边长为b的小正方形 $(a > b)$ ，把余下的部分剪成一个矩形，通过计算两个图形（阴影部分）的面积，验证了一个等式是（）

A、 $a^{2} - b^{2} = (a + b) (a - b)$ B、 $(a + b)^{2} = a^{2} + 2 a b + b^{2}$ C、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$ D、 $(a + 2 b) (a - b) = a^{2} + a b - 2 b^{2}$

查看试题解析
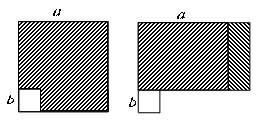8. 学校用24000元和15000元分别购买了相同本数的科普类图书和文学类图书.已知科普类图书平均每本价格比文学类图书的平均每本价格多9元.设文学类图书的平均每本价格为x元，则下列列出的方程中正确的是（）

A、 $\frac{24000}{x} = \frac{15000}{x - 9}$ B、 $\frac{24000}{x - 9} = \frac{15000}{x}$ C、 $\frac{24000}{x} = \frac{15000}{x} + 9$ D、 $\frac{24000}{x + 9} = \frac{15000}{x}$

查看试题解析
9. 如图，下列关于 $∠ A$ ， $∠ B$ ， $∠ C$ ， $∠ 1$ 的关系中一定成立的是（）

A、 $∠ A + ∠ B = ∠ C + ∠ 1$ B、 $∠ A + ∠ 1 = ∠ B + ∠ C$ C、 $∠ A + ∠ B + ∠ C = ∠ 1$ D、 $∠ A + ∠ B + ∠ C + ∠ 1 = 360 °$

查看试题解析
10. 我们知道…，2^-3= $\frac{1}{8}$ ， 2^-2= $\frac{1}{4}$ ， 2^-1= $\frac{1}{2}$ ， 2⁰=1，2¹=2，2²=4，2³=8，….如果要把指数推广到有理数，则2^-0.5=（）

A、 $- 0.5$ B、2 C、 $\frac{1}{\sqrt{2}}$ D、 $\sqrt{2}$

查看试题解析

二、填空题

11. 因式分解： $2 a^{2} - 4 a =$ .

查看试题解析
12. 分式 $\frac{2 x - 3}{2 x + 3}$ 有意义的条件是.

查看试题解析
13. 如图，在 $△ A B C$ 中，直线 $D E$ 是边 $A C$ 的垂直平分线，连接 $A E$ ，若 $A B = 3 ， B C = 5$ ，则 $△ A B E$ 的周长为.

查看试题解析
14. 如图，在 $△ A B C$ 中，D是 $B C$ 上的一点， $C A = C D$ ， $C E$ 平分 $∠ A C B$ ，交 $A B$ 于点E ，连接 $D E$ ，若 $∠ A = 100 °$ ， $∠ B = 45 °$ ，则 $∠ B E D =$ $°$ .

查看试题解析
15. 如图，在 $△ A B C$ 中， $A B = A C$ ， $A D ⊥ B C$ ，垂足为D ， $C E = 3 A E$ ，连接 $B E$ 交 $A D$ 于点F ，连接 $C F$ ，若 $△ C E F$ 的面积为3，则 $△ A B F$ 的面积为， $△ C D F$ 的面积为.

查看试题解析
16. 如图， $△ A B C$ 是等腰直角三角形， $∠ A B C = 90 °$ ，将 $△ A B C$ 沿着一条直线折叠，使顶点A的对应点 $A^{'}$ 刚好落在边 $B C$ 上，这条折痕分别交 $A B$ ， $A C$ 于点D ， E. $∠ A B C$ 的平分线交 $A^{'} D$ 于点F ，连接 $E F$ ，若 $C E = A^{'} B$ ，则 $∠ A^{'} E F =$ $°$ .

查看试题解析

三、解答题

17. 计算：

(1)、 $3^{- 2} + 12^{0}$ ；

(2)、 $\frac{1}{4} x^{2} y^{3} z \div {(2 x y)}^{2}$ .

查看试题解析
18. 计算： ${(2 x - y)}^{2} - {(x - 2 y)}^{2}$ .

查看试题解析
19. 化简： $(\frac{1}{x - 2} - \frac{1}{x + 2}) \div \frac{2}{x - 2}$ ，并求当 $x = 3$ 时这个代数式的值.

查看试题解析
20. 如图， $△ A B C$ 的顶点分别为 $A (1 ， 3) ， B (4 ， 5) ， C (1 ， 5)$ ，先将 $△ A B C$ 以第一象限的角平分线所在直线为对称轴通过轴对称得到 $△ A^{'} B^{'} C^{'}$ ，再将 $△ A^{'} B^{'} C^{'}$ 以x轴为对称轴通过轴对称得到△ $A^{″} B^{″} C^{″}$ .

(1)、画出 $△ A^{″} B^{″} C^{″}$ ；

(2)、写出 $A^{″} ， B^{″} ， C^{″}$ 三点的坐标；

(3)、一般地，某一点 $P (x ， y)$ 经过这样的两次轴对称变换后得到的点 $P^{″}$ 的坐标为.

查看试题解析
21. 如图，四边形 $A B C D$ 中， $A B ∥ C D$ ， $A B = C D$ . $A D$ 与 $C B$ 有什么关系？证明你的结论.

查看试题解析
22. 如图，河l同侧有一块直角三角形的绿化带 $A B C$ ， $∠ C = 90 °$ ， $∠ B = 30 °$ ， $B C = 40 m$ ， $C A ⊥ l$ .A到河l的距离等于 $C A$ 的长度.需要用水管从河l上一点P处分别引水到A ， B两处，并通过安装在这两处的喷水龙头灌溉草地.

(1)、请在河l上画出点P的位置，使得从点P向A ， B两处引水所需的水管总长度最短；

(2)、求至少需要水管多少米（连接处接头长度忽略不计）.

查看试题解析
23. 某公司生产一种工件，通过自动化技术改造，既增加了每周的产量，又提高了产品的优等率.

(1)、技术改造的前后两周，该公司生产的这种产品的优等率分别为 $80 %$ 和 $98 %$ ，这两周生产的产品的平均优等率会是 $\frac{80 % + 98 %}{2} = 89 %$ 吗？设出必要的字母表示相关的量，通过计算说明理由.

(2)、如果技术改造前一周的产量为500件，产品优等率为 $80 %$ ；技术改造后一周的产品的优等率提高到了 $98 %$ .这样，这两周生产的产品的平均优等率达到 $90 %$ .问：技术改造后一周的产量比技术改造前一周增加了多少件？

查看试题解析
24. 如图， $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 30 °$ ，射线 $A M$ 与射线 $A C$ 关于直线 $A B$ 对称.E是 $A M$ 上的一点，连接 $C E$ 交 $A B$ 于点D.

(1)、若 $C E ⊥ A M$ ，求证： $△ A D C$ 是等腰三角形；

(2)、若 $A E = A D$ ，连接 $B E$ ，求 $∠ A B E$ 的度数；

(3)、若 $B E = B C$ ，求 $∠ A C E$ 的度数.

查看试题解析