浙江省台州市椒江区2021-2022学年七年级上学期期末数学试题
试卷更新日期:2022-11-16 类型:期末考试
一、单选题
-
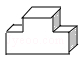
1. 如图所示的工件是由两个长方体构成的组合体,则它的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 2021年11月19号,椒江过江隧道项目新闻发布会召开,项目总投资约41亿,其中数据41亿用科学记数法表示为( )A、 B、 C、 D、3. 如图, , 是数轴上的两个有理数,下面说法中正确的是( )
2. 2021年11月19号,椒江过江隧道项目新闻发布会召开,项目总投资约41亿,其中数据41亿用科学记数法表示为( )A、 B、 C、 D、3. 如图, , 是数轴上的两个有理数,下面说法中正确的是( ) A、 B、 C、 D、4. 下列对的描述错误的是( )A、它是一个单项式 B、它和是同类项 C、它的次数是5 D、它的系数是5. 已知a=b,下列等式不一定成立的是( )A、a+c=b+c B、c﹣a=c﹣b C、ac=bc D、6. 如图,货轮在航行过程中,发现灯塔在它南偏西的方向上,同时货轮在它北偏东的方向上,则此时的大小是( )
A、 B、 C、 D、4. 下列对的描述错误的是( )A、它是一个单项式 B、它和是同类项 C、它的次数是5 D、它的系数是5. 已知a=b,下列等式不一定成立的是( )A、a+c=b+c B、c﹣a=c﹣b C、ac=bc D、6. 如图,货轮在航行过程中,发现灯塔在它南偏西的方向上,同时货轮在它北偏东的方向上,则此时的大小是( ) A、 B、 C、 D、7. 某校男生人数占学生总数的 , 女生的人数是 , 学生的总数是( )A、 B、 C、 D、8. 现有30个数,其中所有正数之和为10,负数之和为 , 这30个数的绝对值之和为( )A、 B、 C、 D、9. 在编写数学谜题时,“”内要求填写同一个数字,若“”内数字为 , 则列出方程正确的是( )A、 B、 C、 D、10. 如图,有3种大小不同的7张正方形纸片和1张长方形纸片②,将它们铺满长方形桌面,重叠部分(图中阴影部分)是个正方形,若要求长方形桌面长与宽的差,只需知道( )
A、 B、 C、 D、7. 某校男生人数占学生总数的 , 女生的人数是 , 学生的总数是( )A、 B、 C、 D、8. 现有30个数,其中所有正数之和为10,负数之和为 , 这30个数的绝对值之和为( )A、 B、 C、 D、9. 在编写数学谜题时,“”内要求填写同一个数字,若“”内数字为 , 则列出方程正确的是( )A、 B、 C、 D、10. 如图,有3种大小不同的7张正方形纸片和1张长方形纸片②,将它们铺满长方形桌面,重叠部分(图中阴影部分)是个正方形,若要求长方形桌面长与宽的差,只需知道( ) A、正方形①的边长 B、长方形②的周长 C、正方形③的边长 D、正方形④的边长
A、正方形①的边长 B、长方形②的周长 C、正方形③的边长 D、正方形④的边长二、填空题
-
11. -3-π (填“”“”“”).12. 若关于的方程与的解互为相反数,则的值为 .13. 图1是2022年1月的月历,图2为月历中任意框出的9个数,请你用一个等式表示 , , 之间的关系: .
 14. 如图,将长方形纸片分别沿 , 折叠,点 , 恰好重合于点 , , 则 .
14. 如图,将长方形纸片分别沿 , 折叠,点 , 恰好重合于点 , , 则 . 15. 如图是“跳格子游戏”用的格子,每个格子都有一个对应的数字.游戏规则是:棋子若停在奇数的格上,则下次沿顺时针方向跳5格;若停在偶数的格上,则下次沿逆时针方向跳1格.若棋子从表示数1的格子开始,第1次跳到6,第2次跳到5,第225次它会跳到表示数的格子上.若次跳动所经过的所有数字之和为459,则 .
15. 如图是“跳格子游戏”用的格子,每个格子都有一个对应的数字.游戏规则是:棋子若停在奇数的格上,则下次沿顺时针方向跳5格;若停在偶数的格上,则下次沿逆时针方向跳1格.若棋子从表示数1的格子开始,第1次跳到6,第2次跳到5,第225次它会跳到表示数的格子上.若次跳动所经过的所有数字之和为459,则 .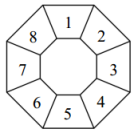
三、解答题
-
16. .17. 计算:(1)、 ;(2)、 ;18. 解方程:(1)、 ;(2)、 .19. 先化简,再求值: , 其中 , .20. 如图,点A,B分别表示数a,b(要求:尺规作图,不写作法,保留作图痕迹).
 (1)、在数轴上作出表示数的点C;(2)、在数轴上作出表示数的点D.21. 食品厂为检测某袋装食品的质量是否符合标准,从袋装食品中抽出样品30袋,每袋以100克为标准质量,超过和不足100克的部分分别用正、负数表示,记录如下:
(1)、在数轴上作出表示数的点C;(2)、在数轴上作出表示数的点D.21. 食品厂为检测某袋装食品的质量是否符合标准,从袋装食品中抽出样品30袋,每袋以100克为标准质量,超过和不足100克的部分分别用正、负数表示,记录如下:与标准质量的差值/克
-4
-2
0
1
2
3
袋数
3
4
6
8
6
3
(1)、在抽测的样品中,任意挑选两袋,它们的质量最大相差多少克?(2)、食品袋中标有“净重克”,这批抽样食品中共有几袋质量合格?请你计算出这30袋食品的合格率;(3)、这批样品的平均质量比每袋的标准质量多(或少)多少克?22. 已知点 , 为线段上两点, , . (1)、如图1,若点是线段中点,求的长;(2)、如图2,若点 , 分别是 , 的中点,求的长.23. 甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,两超市各自推出了不同的优惠方案:
(1)、如图1,若点是线段中点,求的长;(2)、如图2,若点 , 分别是 , 的中点,求的长.23. 甲、乙两家超市以相同的价格出售同样的商品,为了吸引顾客,两超市各自推出了不同的优惠方案:甲超市:在该超市累计购买商品超出300元之后,超出部分按原价的8折优惠;
乙超市:在该超市累计购买商品超出200元之后,超出部分按原价的8.5折优惠.
(1)、当累计购物500元时,选择哪家超市购买更优惠?请说明理由;(2)、当累计购物多少元时,在甲、乙两家超市所需支付的费用相同?(3)、小明发现去甲、乙两家超市买同样的商品,乙超市比甲超市便宜12元,小明选择了去乙超市购买,则小明花的钱是元.24. 如图1,点为直线上一点,将一副三角板的各一锐角顶点放在点上,边 , 分别在射线 , 上,其中 , , , 将三角板绕点以每秒的速度逆时针旋转. (1)、如图2,三角板旋转到的内部.
(1)、如图2,三角板旋转到的内部.①当恰好平分时,求旋转时间以及的度数;
②的度数是否为定值?若是,求出该定值;若不是,请说明理由.
(2)、在三角板开始旋转的同时,三角板绕点以每秒的速度顺时针开始旋转,当三角板旋转时两个三角板都停止运动,在运动过程中,当时,请直接写出所有符合条件的运动时间(本题中所研究的角都是小于等于的角).