浙江省绍兴市上虞区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-11-16 类型:期末考试
一、单选题
-
1. 下面给出的四个三角形都有一部分被遮挡,其中不能判定三角形类型的是( )A、
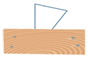 B、
B、 C、
C、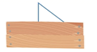 D、
D、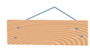 2. 下列图形中,不是轴对称图形的是()A、
2. 下列图形中,不是轴对称图形的是()A、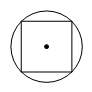 B、
B、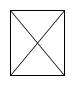 C、
C、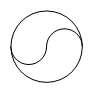 D、
D、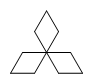 3. 如果m>n,那么下列结论错误的是( )A、m+2>n+2 B、﹣2m>﹣2n C、2m>2n D、m﹣2>n﹣24. 在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标为( )A、 B、 C、 D、5. 不等式组 的解集在数轴上表示为( ).A、
3. 如果m>n,那么下列结论错误的是( )A、m+2>n+2 B、﹣2m>﹣2n C、2m>2n D、m﹣2>n﹣24. 在平面直角坐标系的第四象限内有一点M,到x轴的距离为4,到y轴的距离为5,则点M的坐标为( )A、 B、 C、 D、5. 不等式组 的解集在数轴上表示为( ).A、 B、
B、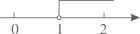 C、
C、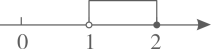 D、
D、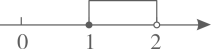 6. 下列命题中,是假命题的是()A、两点确定一条直线 B、对于任何实数x , 有 C、三角形三个内角的和等于180° D、三角形的两边之和大于第三边7. 如图,BD平分∠ABC交AC于点D.若 , 则∠ADB=( )
6. 下列命题中,是假命题的是()A、两点确定一条直线 B、对于任何实数x , 有 C、三角形三个内角的和等于180° D、三角形的两边之和大于第三边7. 如图,BD平分∠ABC交AC于点D.若 , 则∠ADB=( )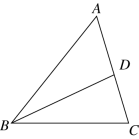 A、100° B、105° C、110° D、120°8. 如图是2×5的正方形网格,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形.则在网格中,能画出且与△ABC成轴对称的格点三角形一共有()个.
A、100° B、105° C、110° D、120°8. 如图是2×5的正方形网格,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形.则在网格中,能画出且与△ABC成轴对称的格点三角形一共有()个.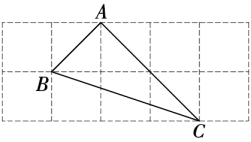 A、1 B、2 C、3 D、49. 已知点A(x , y)在直线上,且.则下列不等式成立的是( )A、 B、 C、 D、10. 早上8点,妈妈把小明送到游泳馆训练,之后马上回家准备午饭,烧好饭后去游泳馆等小明训练结束接其回家,妈妈两次从游泳馆回家的驾车速度相同,在家做饭和在游泳馆等小明的时间也相同.8点开始,妈妈离家的距离y关于时间x的函数图象如图所示,则妈妈从家出发去游泳馆等小明的路途中间的时刻(即图象中CD中点G所在的时刻)为( )
A、1 B、2 C、3 D、49. 已知点A(x , y)在直线上,且.则下列不等式成立的是( )A、 B、 C、 D、10. 早上8点,妈妈把小明送到游泳馆训练,之后马上回家准备午饭,烧好饭后去游泳馆等小明训练结束接其回家,妈妈两次从游泳馆回家的驾车速度相同,在家做饭和在游泳馆等小明的时间也相同.8点开始,妈妈离家的距离y关于时间x的函数图象如图所示,则妈妈从家出发去游泳馆等小明的路途中间的时刻(即图象中CD中点G所在的时刻)为( )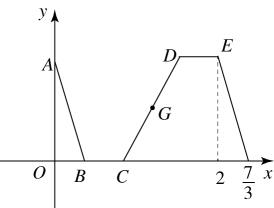 A、9点 B、9点10分 C、9点20分 D、9点30分
A、9点 B、9点10分 C、9点20分 D、9点30分二、填空题
-
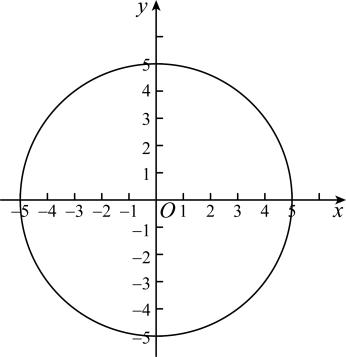
11. 如图,在平面直角坐标系中,以原点为圆心,5个单位长度为半径画圆,则此圆与y轴的两个交点间的距离是.
 12. 已知正比例函 , 当时,.则比例系数k=.13. 某个关于x的不等式的解集在数轴上的表示如图所示,这个不等式的解集是 .
12. 已知正比例函 , 当时,.则比例系数k=.13. 某个关于x的不等式的解集在数轴上的表示如图所示,这个不等式的解集是 . 14. 已知点A(2,5),B( , 3),C(-5,2),D(-0.5,).则在这些点中,在如图所示的直角坐标系阴影区域内的点有.
14. 已知点A(2,5),B( , 3),C(-5,2),D(-0.5,).则在这些点中,在如图所示的直角坐标系阴影区域内的点有.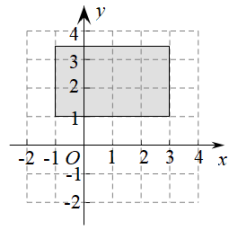 15. 已知线段AB=6cm,作AB的中垂线CD , 垂足为M , 在CD上取点N , 使MN=4cm,连结AN , BN , 则△ABN的周长为cm.16. 如图是折叠式沙发椅的示意图,相关数据标注在图中AE与BD的交点为C , 且∠A , ∠B , ∠E保持不变,为更舒适需调整∠D的大小,使 , 则图中∠D应(填“增加”或“减少”)度.
15. 已知线段AB=6cm,作AB的中垂线CD , 垂足为M , 在CD上取点N , 使MN=4cm,连结AN , BN , 则△ABN的周长为cm.16. 如图是折叠式沙发椅的示意图,相关数据标注在图中AE与BD的交点为C , 且∠A , ∠B , ∠E保持不变,为更舒适需调整∠D的大小,使 , 则图中∠D应(填“增加”或“减少”)度.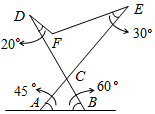 17. 等边△ABC的边长为2,过点C作直线lAB , P为直线l上一点,且 , 则点P到BC所在直线的距离是.18. 如图,等腰直角△ABC中,D为斜边AB的中点,E , F分别为腰AC , BC上(异于端点)的点,DE⊥DF , AB=10,设x=DE+DF , 则x的取值范围是.
17. 等边△ABC的边长为2,过点C作直线lAB , P为直线l上一点,且 , 则点P到BC所在直线的距离是.18. 如图,等腰直角△ABC中,D为斜边AB的中点,E , F分别为腰AC , BC上(异于端点)的点,DE⊥DF , AB=10,设x=DE+DF , 则x的取值范围是.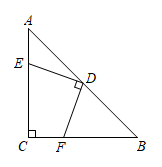
三、解答题
-
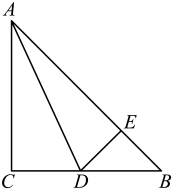
19. 解答下列各题:(1)、解不等式;(2)、把点A(a , -3)向左平移3个单位,所得的点与点A关于y轴对称,求a的值.20. 如图,在△ABC中,∠C=90°,AC=BC=1,AD是∠BAC的平分线,DE⊥AB , 垂足为E.求BE的长.
 21. 如图,正方形EFGH的四个顶点分别在边长为1的正方形ABCD的四条边上.
21. 如图,正方形EFGH的四个顶点分别在边长为1的正方形ABCD的四条边上. (1)、设 , 试求正方形EFGH的面积y关于x的函数式,并写出自变量x的取值范围;(2)、当时,求正方形EFGH的面积.22. 已知,在 中, ,点D,点E在BC上, ,连接 .
(1)、设 , 试求正方形EFGH的面积y关于x的函数式,并写出自变量x的取值范围;(2)、当时,求正方形EFGH的面积.22. 已知,在 中, ,点D,点E在BC上, ,连接 .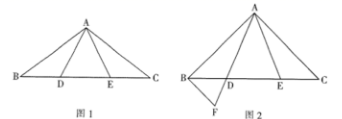 (1)、如图1,求证: ;(2)、如图2,当 时,过点B作 ,交AD的延长线于点F,在不添加任何辅助线的情况下,请直接写出图2中四个等腰三角形,使写出的每个等腰三角形的顶角都等于45°.23. 元旦期间,某移动公司就手机流量套餐推出三种优惠方案,具体如下表所示:A , B , C三种方案,每月所需的费用y(元)与每月使用的流量x(GB)之间的函数关系如图所示(已知).解答下列问题
(1)、如图1,求证: ;(2)、如图2,当 时,过点B作 ,交AD的延长线于点F,在不添加任何辅助线的情况下,请直接写出图2中四个等腰三角形,使写出的每个等腰三角形的顶角都等于45°.23. 元旦期间,某移动公司就手机流量套餐推出三种优惠方案,具体如下表所示:A , B , C三种方案,每月所需的费用y(元)与每月使用的流量x(GB)之间的函数关系如图所示(已知).解答下列问题A方案
B方案
C方案
每月基本费用(元)
20
56
188
每月免费试用流量(GB)
10
m
无限
超出后每GB收费(元)
n
n
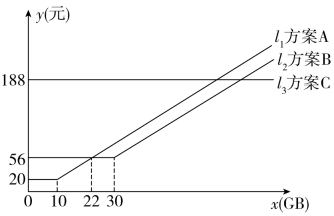 (1)、填空:表中的m= , n=;(2)、在A方案中,若每月使用的流量不少于10GB,求每月所需的费用y(元)与每月使用的流量x(GB)之间的函数关系式;(3)、在这三种方案中,当每月使用的流量超过多少GB时,选择C方案最划算?24. 如图,在射线MB上,MB=10,A是射线外一点,AB=5,且A到射线MB的距离AC=3,动点P从点M出发,沿射线MB方向以1个单位/秒的速度运动,设点P运动的时间为t秒.解答下列问题.
(1)、填空:表中的m= , n=;(2)、在A方案中,若每月使用的流量不少于10GB,求每月所需的费用y(元)与每月使用的流量x(GB)之间的函数关系式;(3)、在这三种方案中,当每月使用的流量超过多少GB时,选择C方案最划算?24. 如图,在射线MB上,MB=10,A是射线外一点,AB=5,且A到射线MB的距离AC=3,动点P从点M出发,沿射线MB方向以1个单位/秒的速度运动,设点P运动的时间为t秒.解答下列问题.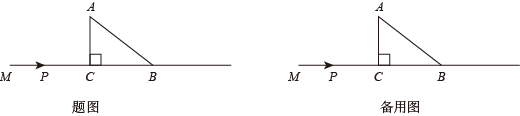 (1)、当t为何值时,△PAB是等腰三角形;(2)、当t为何值时,△PAB是直角三角形.
(1)、当t为何值时,△PAB是等腰三角形;(2)、当t为何值时,△PAB是直角三角形.