浙江省衢州市衢江区2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，点(1，2)所在的象限是（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 下列长度的三条线段能构成三角形的是（　　）

A、1，2，3 B、5，10，13 C、4，5，10 D、2，3，6

查看试题解析
3. 不等式2x≤4的解集在数轴上表示为（　　）

A、 B、 C、 D、

查看试题解析
4. 等腰三角形的底角为50°，则它的顶角度数是（　　）

A、50° B、80° C、65°或80° D、50°或80°

查看试题解析
5. 已知 $△ A B C$ 中， $A C = 3$ ， $A B = 5$ ， $∠ C = 90 °$ ，则 $△ A B C$ 的周长等于（）

A、11 B、 $8 + \sqrt{34}$ C、12 D、13

查看试题解析
6. 能使命题“a＞b ，则a²＞b²”为假命题的是（　　）

A、a＝-2，b＝-1 B、a＝-2，b＝-3 C、a＝3，b＝-2 D、a＝2，b＝-1

查看试题解析
7. 关于一次函数 $y = - x + 1$ 的描述，下列说法正确的是（）

A、图象经过点 $(- 2 ， 1)$ B、图象经过第一、二、三象限 C、y随x的增大而增大 D、图象与y轴的交点坐标是 $(0 ， 1)$

查看试题解析
8. 一辆汽车沿A地北偏东50°方向行驶5千米到达B地，再沿B地南偏东10°方向行驶5千米到达C地，则此时A、C两地相距（　　）千米

A、10 B、5 $\sqrt{3}$ C、5 $\sqrt{2}$ D、5

查看试题解析
9. 对一实数x按如图所示程序进行操作，规定：程序运行从“输入一个实数x”到“判断结果是否大于190？”为一次操作，如果操作恰好进行两次后停止，则x的取值范围是（　　）

A、x＜64 B、x＞22 C、22＜x≤64 D、22＜x＜64

查看试题解析
10. 如图，将三角形纸片ABC沿AD折叠，使点C落在BD边上的点E处.若∠C＝45°，∠B＝30°，AD＝2，则AB²-AC²的值是（　　）

A、8 B、12 C、16 D、24

查看试题解析

二、填空题

11. 写出一个不等式，使它的解为x＞-1，则这个不等式可以是 .

查看试题解析
12. 点A（-2，3）到x轴的距离是 .

查看试题解析
13. 如图，在△ABC中，∠ACD＝125°，∠B＝40°，则∠A的度数是 .

查看试题解析
14. 如图，若Rt△ADE≌Rt△ACB ， AD＝3，AB＝5，则BC的长是.

查看试题解析
15. 某业主贷款22000元购进一台机器，生产某种产品.已知产品的成本每个5元，售价是每个8元，应付的税款和其他费用是售价的10%.若每月能生产、销售2000个产品，问至少个月后能赚回这台机器的贷款.

查看试题解析
16. 如图，在平面直角坐标系中，直线y $= \frac{3}{4}$ x $+ \frac{3}{2}$ 与x轴交于点A ，且经过点B（2，a），在y轴上有一动点P ，直线BC上有一动点M ，已知C（3，0）.

(1)、a＝；

(2)、若△APM是以线段AM为斜边的等腰直角三角形，则点M的坐标是 .

查看试题解析

三、解答题

17. 解不等式组： ${\begin{array}{l} 2 x + 1 \leq 5 ， \\ - 1 + x > 0 ． \end{array}$

查看试题解析
18. 如图，在△ABC中，点A（-3，1），B（-1，0）.

( 1 )根据上述信息在图中画平面直角坐标系，并求出△ABC的面积；

( 2 )在平面直角坐标系中，作出△ABC关于y轴对称图形△A₁B₁C₁.

查看试题解析
19. 如图，在△ABC中，∠B=40°，∠C=50°．

(1)、通过观察尺规作图的痕迹，可以发现直线DF是线段AB的，射线AE是∠DAC的．

(2)、求∠DAE的度数．

查看试题解析
20. 如图， $∠ B A C = 90 °$ ，AD是 $∠ B A C$ 内部一条射线，若 $A B = A C$ ， $B E ⊥ A D$ 于点E， $C F ⊥ A D$ 于点F.求证： $A F = B E$ .

查看试题解析
21. 如图，平面直角坐标系中，直线y $= \frac{2}{3}$ x+2与经过A（4，0），B（0，4）两点的直线交于P ，且与x轴，y轴分别交于点C和点D.

(1)、求直线AB表达式及点P的坐标；

(2)、设点E在y轴负半轴上，且与点A ， B构成等腰三角形，请求写出点E的坐标.

查看试题解析
22. 在一条笔直的公路上，依次有A、C、B三地，甲、乙两人同时出发，甲从A地骑自行车匀速去B地，途经C地时因事停留1分钟，继续按原速骑行至B地，甲到达B地后，立即按原路原速返回A地；乙步行匀速从B地至A地.甲乙两人距A地的距离y（米）与时间x（分）之间的函数关系如图所示，请结合图象回答下列问题：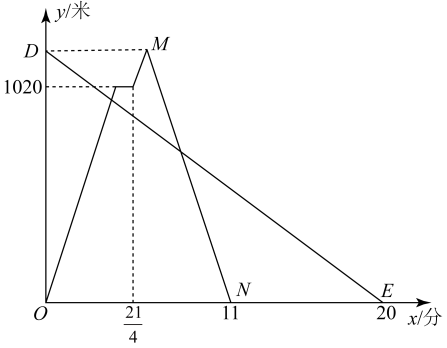

(1)、甲的骑行速度为米/分，点M的坐标为 .

(2)、求甲返回时距A地的距离y（米）与时间x（分）之间的函数表达式（不需要写出自变量的取值范围）；

(3)、甲返回A地的过程中，x为多少时甲追上乙？

查看试题解析
23. 如图是一种单肩包，其背带由双层部分、单层部分和调节扣构成.小文购买时，售货员演示通过调节扣加长或缩短单层部分的长度，可以使背带的长度（单层部分与双层部分长度的和，其中调节扣所占长度忽略不计）加长或缩短，设双层部分的长度为 $x cm$ ，单层部分的长度为 $y cm$ .经测量，得到下表中数据.

双层部分长度 $x (cm)$

2

8

14

20

单层部分长度 $y (cm)$

148

136

124

112

(1)、根据表中数据规律，求出y与x的函数关系式；

(2)、按小文的身高和习惯，背带的长度调为 $130cm$ 时为最佳背带长.请计算此时双层部分的长度；

(3)、设背带长度为 $L cm$ ，求L的取值范围.

查看试题解析
24. 两个顶角相等的等腰三角形，如果具有公共的顶角顶点，并将它们的底角顶点分别对应连接起来得到两个全等三角形，我们把这样的图形称为“手拉手”图形.如图1，在“手拉手”图形中，AB＝AC ， AD＝AE ， ∠BAC＝∠DAE ，连接BD ， CE ，则△ABD≌△ACE.

(1)、请证明图1的结论成立；

(2)、如图2，△ABC和△AED是等边三角形，连接BD ， EC交于点O ，求∠BOC的度数；

(3)、如图3，AB＝BC ， ∠ABC＝∠BDC＝60°，试探究∠A与∠C的数量关系.

查看试题解析

双层部分长度 $x (cm)$	2	8	14	20
单层部分长度 $y (cm)$	148	136	124	112