浙江省宁波市奉化区2021-2022学年八年级上学期期末数学试题
试卷更新日期：2022-11-16 类型：期末考试
一、单选题
-
1. 下列科学防控“新冠肺炎”的图片中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 已知两条线段a＝12cm，b＝5cm，下列线段能和a，b首尾顺次相接组成三角形的是（ ）A、18cm B、12cm C、7cm D、5cm3. 已知a＞b，则下列各式中一定成立的是（ ）A、a﹣b＜0 B、﹣a+1＞﹣b+1 C、a﹣2＞b﹣2 D、ac＞bc4. 在平面直角坐标系xOy中，点M（﹣4，3）到x轴的距离是（ ）A、﹣4 B、4 C、5 D、3.5. 一次函数 的图象大致是（ ）A、
B、
C、
D、
6. 如图，在 和 中， ，添加一个条件，不能证明 和 全等的是（ ）
A、 B、 C、 D、7. 如图，在△ABC中，AB的垂直平分线分别交AB、BC于点D、E，连接AE，若AE＝4，EC＝2，则BC的长是（ ）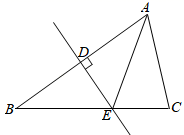
A、2 B、4 C、6 D、88. 某次知识竞赛共20道题，每一题答对得10分，不答得0分，答错扣5分，小聪有一道题没答，竞赛成绩超过90分.设他答对了x道题，则根据题意可列出不等式为（ ）A、10x﹣5（19﹣x）≥90 B、10x﹣5（19﹣x）＞90 C、10x﹣（19﹣x）≥90 D、10x﹣（19﹣x）＞909. 如图， 、 、 、 是四根长度均为5cm的火柴棒，点A、C、E共线.若 ， ，则线段 的长度为（ ）
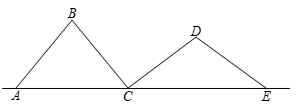A、6 cm B、7 cm C、 D、8cm10. △DEF和△GHK均为等边三角形，将它们按如图1、图2的方式放置在等边三角形ABC内，若求图1、图2中的阴影部分面积的和，则只需知道（ ）
A、△BDE的面积 B、四边形BEFD的面积 C、△ABC面积 D、△DGH的面积二、填空题
-
11. 已知一次函数y＝kx﹣1（k≠0），若y随x的增大而减小，请你写出符合条件的k的一个值：.12. 命题“如果a+b=0，那么a，b互为相反数”的逆命题为.13. 如图，某研究性学习小组为测量学校A与河对岸水上乐园B之间的距离，在学校附近选一点C，利用测量仪器测得∠A＝60°，∠C＝90°，AC＝1km.据此，可求得学校与水上乐园之间的距离AB等于 km.
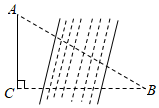14. 如图，在中，是边上的高，平分 ， 交于点E， ， 若的面积为5，则的长为.
15. 如图，函数和的图象相交于点 ， 则关于x的不等式的解为.
16. 如图，在Rt△ABC中，AC＝BC＝1，D是斜边AB上一点（与点A，B不重合），将△BCD绕着点C旋转90°到△ACE，连结DE交AC于点F，若△AFD是等腰三角形，则AF的长为 .
三、解答题
-
17. 解不等式组.18. 已知点分别根据下列条件求出点P的坐标.(1)、点P在x轴上；(2)、点Q的坐标为（1，5），直线PQ∥y轴；19. 如图，D是的边上一点，// ， 交于E点，.
(1)、求证：.(2)、若 ， ， 求的长.20. 如图，△ABC（∠B＞∠A）．
(1)、在边AC上用尺规作图作出点D，使∠CDB=2∠A（保留作图痕迹）；(2)、在（1）的情况下，连接BD，若CB=CD，∠A=35°，求∠C的度数．21. 在平面直角坐标系xOy中，已知点A（2，0），动点P（x，y）在第一象限，且x+y＝8，△OPA的面积为S.(1)、求S关于x的函数表达式和x的取值范围.(2)、求当S＝2时点P的坐标.(3)、OP+PA的最小值为.22. 某班计划购买A、B两款文具盒作为期末奖品.若购买3盒A款的文具盒和1盒B款的文具盒需用22元；若购买2盒A款的文具盒和3盒B款的文具盒需用24元.(1)、每盒A款的文具盒和每盒B款的文具盒各多少元.(2)、某班决定购买以上两款的文具盒共40盒，总费用不超过210元，那么该班最多可以购买多少盒A款的文具盒？23. 为了更好地亲近大自然，感受大自然的美好风光，小聪和小慧去某风景区游览，景区入口与观景点之间的路程为3千米，他们约好在观景点见面.小聪步行先从景区入口处出发，中途休息片刻后继续以原速度前行，此时小慧乘观光车从景区入口处出发，他们沿相同路线先后到达观景点，如图，分别表示小聪与小慧离景区入口的路程y（千米）与小聪离开的时间x（分）之间的关系.根据图象解决下列问题：
(1)、小聪步行的速度是（千米/分），中途休息分钟；(2)、求小慧离景区入口的路程y（千米）关于小聪离开的时间x（分）的函数表达式；(3)、小慧比小聪早几分钟到达观景点？请说明理由.24.
(1)、【证明体验】如图1，在中，为边上的中线，延长至E，使 ， 连接.求证：.(2)、【迁移应用】如图2，在中， ， ， 为的中点，.求面积.
(3)、【拓展延伸】如图3，在中， ， 是延长线上一点， ， F是上一点，连接交于点E，若 ， ， 求的长.