浙江省宁波七中教育集团2021-2022学年八年级上学期期末测试数学试题
试卷更新日期:2022-11-16 类型:期末考试
一、单选题
-
1. 下列汽车标志不是轴对称图形的是()A、
 B、
B、 C、
C、 D、
D、 2. 要说明命题“若 ,则 ”是假命题,能举的一个反例是A、 , B、 , C、 , D、 ,3. 一次函数y=﹣4x+2的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 已知 , 则下列不等式成立的是( )A、 B、 C、 D、5. 在平面直角坐标系中,点平移后能与原来的位置关于y轴对称,则应把点A( )A、向左平移个单位 B、向右平移个单位 C、向下平移个单位 D、向上平移个单位6. 如图,在Rt△ABC中,∠B=90°,分别以A , C为圆心,大于AC长为半径作弧,两弧相交于点M , N , 作直线MN , 与AC , BC分别交于D , E , 连结AE , 若AB=6,AC=10,则△ABE的周长为()
2. 要说明命题“若 ,则 ”是假命题,能举的一个反例是A、 , B、 , C、 , D、 ,3. 一次函数y=﹣4x+2的图象不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 已知 , 则下列不等式成立的是( )A、 B、 C、 D、5. 在平面直角坐标系中,点平移后能与原来的位置关于y轴对称,则应把点A( )A、向左平移个单位 B、向右平移个单位 C、向下平移个单位 D、向上平移个单位6. 如图,在Rt△ABC中,∠B=90°,分别以A , C为圆心,大于AC长为半径作弧,两弧相交于点M , N , 作直线MN , 与AC , BC分别交于D , E , 连结AE , 若AB=6,AC=10,则△ABE的周长为() A、13 B、14 C、15 D、167. 如图是用直尺和圆规作已知角∠AOB平分线OP的示意图,仔细观察,根据三角形全等的知识,说明画出OP的依据是()
A、13 B、14 C、15 D、167. 如图是用直尺和圆规作已知角∠AOB平分线OP的示意图,仔细观察,根据三角形全等的知识,说明画出OP的依据是() A、边角边,全等三角形对应角相等 B、角边角,全等三角形对应角相等 C、边边边,全等三角形对应角相等 D、斜边直角边,全等三角形对应角相等8. 小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )A、
A、边角边,全等三角形对应角相等 B、角边角,全等三角形对应角相等 C、边边边,全等三角形对应角相等 D、斜边直角边,全等三角形对应角相等8. 小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )A、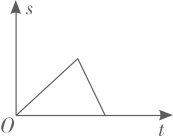 B、
B、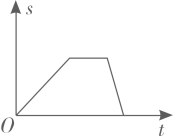 C、
C、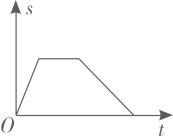 D、
D、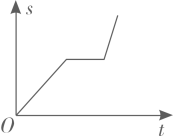 9. 某兴趣小组开展了一次探究活动,过程如下:设 , 现把长度相等的小棒依次摆放在射线AB、AC之间,并使小棒两端分别落在两射线上,从点A1开始,依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.若只能摆放5根小棒,则的范围是( ).
9. 某兴趣小组开展了一次探究活动,过程如下:设 , 现把长度相等的小棒依次摆放在射线AB、AC之间,并使小棒两端分别落在两射线上,从点A1开始,依次向右摆放,其中A1A2为第1根小棒,且A1A2=AA1.若只能摆放5根小棒,则的范围是( ). A、15°<θ<18° B、15°<θ≤18° C、15°≤θ<18° D、15°≤θ≤18°10. 设a , b是任意两个实数,用max{a , b}表示a , b两数中的较大者,例如max{4,3}=4,则max{ , , }的最小值等于( )A、-2 B、1 C、7 D、3
A、15°<θ<18° B、15°<θ≤18° C、15°≤θ<18° D、15°≤θ≤18°10. 设a , b是任意两个实数,用max{a , b}表示a , b两数中的较大者,例如max{4,3}=4,则max{ , , }的最小值等于( )A、-2 B、1 C、7 D、3二、填空题
-
11. 若二次根式 有意义,则x的取值范围是 .12. 化简;.13. 命题“同位角相等,两直线平行”的逆命题是: .14. 已知等腰三角形的一个内角的度数是40°,则它的顶角的度数是 .15. 若一次函数在范围内有最大值17,则k=.16. 已知在△ABC中,AB= 8,BC =5,∠A=30°,则△ABC的面积是.17. 若一元一次不等式的解为 , 则不等式的解为.
三、解答题
-
18.(1)、解不等式组;(2)、计算:.19. 已知:如图∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.求证:MN⊥BD.
 20. 某地计划从甲、乙两个蔬菜基地向A , B两市运送蔬菜.甲、乙两个基地分别可运出80吨和100吨蔬菜.A , B两市分别需要蔬菜110吨和70吨.从甲,乙两基地运往A , B两市的运费单价如下表:
20. 某地计划从甲、乙两个蔬菜基地向A , B两市运送蔬菜.甲、乙两个基地分别可运出80吨和100吨蔬菜.A , B两市分别需要蔬菜110吨和70吨.从甲,乙两基地运往A , B两市的运费单价如下表:A市(元/吨)
B市(元/吨)
甲基地
15
20
乙基地
10
25
设从甲基地运往A市x吨蔬菜时,总运费为y元.
(1)、求y关于x的函数表达式及自变量的取值范围;(2)、当甲基地运往A市多少吨蔬菜时,总运费最省?最省的总运费是多少元?21. 如图,正方形网格中每个小正方形的边长都为1,每一个小格的顶点叫做格点.在4×4的网格中画4个以格点为顶点,且面积等于4的等腰三角形(备注:每个图中各画一个). 22. A、B两地相距480km,甲、乙两人驾车沿同一条公路从A地出发到B地.甲、乙离开A地的路程y(km)与时间x(h)的函数关系如图所示.
22. A、B两地相距480km,甲、乙两人驾车沿同一条公路从A地出发到B地.甲、乙离开A地的路程y(km)与时间x(h)的函数关系如图所示. (1)、分别求出甲、乙离开A地的路程y(km)与时间x(h)的函数解析式及相应自变量的取值范围;(2)、甲出发多少时间后两人相距20km?23. 如图,在△ABC中,AB=2,BC=6,∠B=60°,点P从B点出发向C点运动,在运动过程中,设线段BP的长为x , 设线段AP的长为y.
(1)、分别求出甲、乙离开A地的路程y(km)与时间x(h)的函数解析式及相应自变量的取值范围;(2)、甲出发多少时间后两人相距20km?23. 如图,在△ABC中,AB=2,BC=6,∠B=60°,点P从B点出发向C点运动,在运动过程中,设线段BP的长为x , 设线段AP的长为y. (1)、请填写下表;
(1)、请填写下表;x
0
1
2
3
4
5
6
y
2
2
(2)、在如下平面直角坐标系中,利用表格中的数据画出y关于x的图象;(参考值: , , ) (3)、当AP=2BP时,利用图象判断x的取值范围为( )A、0<x<0.5 B、0.5<x<1 C、1<x<1.5 D、1.5<x<2(4)、当△ABP为钝角三角形时,请直接写出x的取值范围.24. 如图,在平面直角坐标系中,直线分别与x轴,y轴交于A , B两点,把线段AB绕点B顺时针旋转后得到线段BC , 连结AC , OC.
(3)、当AP=2BP时,利用图象判断x的取值范围为( )A、0<x<0.5 B、0.5<x<1 C、1<x<1.5 D、1.5<x<2(4)、当△ABP为钝角三角形时,请直接写出x的取值范围.24. 如图,在平面直角坐标系中,直线分别与x轴,y轴交于A , B两点,把线段AB绕点B顺时针旋转后得到线段BC , 连结AC , OC.
 (1)、当时,求点C的坐标;(2)、当m值发生变化时,△BOC的面积是否保持不变?若不变,计算其大小;若变化,请说明理由;(3)、当S△AOB=2S△BOC时,在x轴上找一点P , 使得△PAB是等腰三角形,求满足条件的所有P点的坐标.25. 定义:如果三角形的两个内角和满足 , 那么我们称这样的三角形为“类直角三角形”.如图,在中, , , .请把这个三角形分割成两个三角形,使得其中一个为“类直角三角形”,并求出这个“类直角三角形”的面积.(备注:要求尺规作图)
(1)、当时,求点C的坐标;(2)、当m值发生变化时,△BOC的面积是否保持不变?若不变,计算其大小;若变化,请说明理由;(3)、当S△AOB=2S△BOC时,在x轴上找一点P , 使得△PAB是等腰三角形,求满足条件的所有P点的坐标.25. 定义:如果三角形的两个内角和满足 , 那么我们称这样的三角形为“类直角三角形”.如图,在中, , , .请把这个三角形分割成两个三角形,使得其中一个为“类直角三角形”,并求出这个“类直角三角形”的面积.(备注:要求尺规作图)