浙江省丽水市莲都区2021-2022学年七年级上学期期末数学试题

试卷更新日期：2022-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 在－5，0，－2，4这四个数中，最小的数是（）

A、－2 B、0 C、－5 D、4

查看试题解析
2. 2021年5月国家统计局公布了第七次人口普查结果，我国人口数约为1412000000，其中数据1412000000用科学记数法表示为（）

A、 $14 .12 \times 10^{8}$ B、 $0.1412 \times 10^{10}$ C、 $1.412 \times 10^{9}$ D、 $1.412 \times 10^{8}$

查看试题解析
3. $2^{3}$ 的意义是（）

A、2×3 B、2＋3 C、2＋2＋2 D、2×2×2

查看试题解析
4. 已知2a＝b＋5，则下列等式中不一定成立的是（）

A、2a－5＝b B、2a＋1＝b＋6 C、a＝ $\frac{b}{2} + \frac{5}{2}$ D、6a＝3b＋5

查看试题解析
5. 如图，射线OA表示北偏东30°方向，射线OB表示北偏西50°方向，则∠AOB的度数是（）

A、60° B、80° C、90° D、100°

查看试题解析
6. 实数x满足 $x^{3} = 71$ ，则下列整数中与x最接近的是（）

A、3 B、4 C、5 D、6

查看试题解析
7. 若 $3 x^{3 m} y^{n}^{－ 1}$ 与 $- x^{3} y$ 是同类项，则m－2n的值为（）

A、1 B、0 C、－1 D、－3

查看试题解析
8. 小王准备从A地去往B地，打开导航，显示两地距离为50km，但导航提供的三条可选路线长却分别为56km，66km，61km（如图）．能解释这一现象的数学知识是（）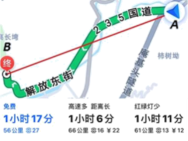

A、两点之间，线段最短 B、垂线段最短 C、两点之间，直线最短 D、两点确定一条直线

查看试题解析
9. 学校组织植树活动，已知在甲处植树的有23人，在乙处植树的有17人，现调20人去支援，使在甲处植树的人数是乙处植树人数的2倍，设应调往甲处x人，则可列方程为（）

A、 $2 (23 + x) = 17 + 20 - x$ B、 $23 + x = 2 (17 + 20 - x)$ C、 $23 + x = 2 (17 + x)$ D、 $23 + 20 - x = 2 (17 + x)$

查看试题解析
10. 长方形ABCD可以分割成如图所示的七个正方形．若AB＝10，则AD的长为（）

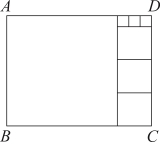A、13 B、11 C、 $\frac{40}{3}$ D、 $\frac{100}{9}$

查看试题解析

二、填空题

11. 2022的相反数为.

查看试题解析
12. 请写出一个无理数．

查看试题解析
13. 定义运算法则： $a \oplus b = a^{2} + a b$ ，例如 $3 \oplus 2 = 3^{2} ＋ 3 \times 2 = 15$ ．若2⊕x＝10，则x的值为．

查看试题解析
14. 如图，P是线段MN上一点，Q是线段PN的中点．若MN=10，MP=6，则MQ的长是．

查看试题解析
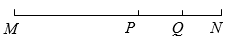15. 请在运算式“6□3□5□9”中的□内，分别填入＋，－，×，÷中的一个符号(不重复使用)，使计算所得的结果最大，则这个最大的结果为．

查看试题解析
16. 某数学兴趣小组在观察等式 $a x^{3} ＋ b x^{2} ＋ c x ＋ d ＝ {(x － 2)}^{3}$ 时发现：当x＝1时， $a ＋ b ＋ c ＋ d ＝ {(1 － 2)}^{3} ＝－ 1$ ；请你解决下列问题：

(1)、－a＋b－c＋d＝；

(2)、8a＋4b＋2c＝．

查看试题解析

三、解答题

17. 计算：

(1)、4＋（－5）×2

(2)、 $\sqrt{9} + {(- 3)}^{2} \times (- \frac{1}{3})$

查看试题解析
18. 解下列方程

(1)、3x＋1＝－2

(2)、 $\frac{y - 1}{3} = 1 - \frac{y + 3}{2}$

查看试题解析
19. 先化简，再求值： $2 (m n - 4 m^{2} - 1) - (3 m^{2} - 2 m n)$ ，其中m＝1，n＝-2.

查看试题解析
20. 如图，已知点A、B、C，按下列要求画出图形．

(1)、作射线BA，直线AC；

(2)、过点B画直线AC的垂线段BH．

查看试题解析
21. 一辆出租车从A站出发，在一条东西走向的道路上行驶，记向东行驶的路程为正，行驶的路程依次为（单位：km）：＋12，－8，＋4，－13，－6，－7．

(1)、通过计算说明出租车是否回到A站；

(2)、若出租车行驶的平均速度为50km/h，则出租车共行驶了多少时间？

查看试题解析
22. 如图，直线AE与CD相交于点B，BF⊥AE．

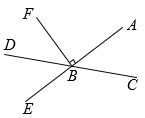(1)、若∠DBE＝60°，求∠FBD的度数；

(2)、猜想∠CBE与∠DBF的数量关系，并说明理由．

查看试题解析

23. 数学活动课上，小聪同学利用列表法探索一次式2x+1、-2x+1的值随着x取值的变化情况．

x	…	-3	-2	-1	0	1	2	3	…
2x+1	…	-5	-3	-1	1				…
-2x+1	…				1	-1	-3	-5	…

(1)、通过计算，完成表格的填写；

(2)、结合表中的数据，当x的值增大时，一次式2x+1，-2x+1的值分别有什么变化？

(3)、请你用类似的方法列表探索二次式

x^{2} + 1

的值随着x取值不断增大的变化情况．

查看试题解析

24. 如图，已知数轴上点A表示的数为10，点B位于点A左侧，AB＝15．动点P从点A出发，以每秒2个单位长度的速度沿数轴向左匀速运动，设运动时间为t秒．

(1)、当点P在A、B两点之间运动时，
①用含t的代数式表示PB的长度；

②若PB＝2PA，求点P所表示的数；

(2)、动点Q从点B出发，以每秒5个单位长度的速度沿数轴向右匀速运动，当点Q到达点A后立即原速返回．若P，Q两点同时出发，其中一点运动到点B时，两点停止运动．求在这个运动过程中，P，Q两点相遇时t的值．

查看试题解析