浙江省丽水市莲都区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-11-16 类型:期末考试
一、单选题
-
1. 在△ABC中,∠A=60°,∠B=50°,则∠C的度数为( )A、60° B、30° C、70° D、50°2. 在以下中国银行、建设银行、工商银行、农业银行图标中,不是轴对称图形的是()A、
 B、
B、 C、
C、 D、
D、 3. 在平面直角坐标系中,点P(1,3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 若x<y , 则下列结论成立的是()A、x+2>y+2 B、-2x<-2y C、3x>3y D、1-x>1-y5. 已知正比例函数y=2x , 下列各点在该函数图象上的是()A、(1,2) B、(2,1) C、(1,) D、(- , 1)6. 不等式的解集在数轴上表示正确的是( )A、
3. 在平面直角坐标系中,点P(1,3)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限4. 若x<y , 则下列结论成立的是()A、x+2>y+2 B、-2x<-2y C、3x>3y D、1-x>1-y5. 已知正比例函数y=2x , 下列各点在该函数图象上的是()A、(1,2) B、(2,1) C、(1,) D、(- , 1)6. 不等式的解集在数轴上表示正确的是( )A、 B、
B、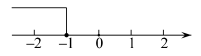 C、
C、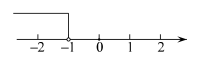 D、
D、 7. 如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是( )
7. 如图,已知AD=AE,添加下列条件仍无法证明△ABE≌△ACD的是( )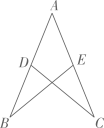 A、AB=AC B、∠B=∠C C、BE=CD D、∠ADC=∠AEB8. 如图,在△ABC中,AB=AC , 分别以点A , C为圆心,大于AC的长为半径画弧,两弧相交于点E、F , 直线EF交BC于点D.连接AD , 已知AC=4,△ABD的周长是10,则BC的长是( )
A、AB=AC B、∠B=∠C C、BE=CD D、∠ADC=∠AEB8. 如图,在△ABC中,AB=AC , 分别以点A , C为圆心,大于AC的长为半径画弧,两弧相交于点E、F , 直线EF交BC于点D.连接AD , 已知AC=4,△ABD的周长是10,则BC的长是( ) A、5 B、6 C、7 D、89. 若一次函数y=(m-1)x+m-2的图象不经过第二象限,则m的取值范围是( )A、m>1 B、m<2 C、1<m<2 D、1<m≤210. 如图,牧童在A处牧马,牧童的家在B处,A , B处到河岸的距离分别是AC=300m,BD=500m,且C , D两地之间的距离为600m.牧童从A处将马牵到河边去饮水,再牵回家,他至少要走的路程是( )
A、5 B、6 C、7 D、89. 若一次函数y=(m-1)x+m-2的图象不经过第二象限,则m的取值范围是( )A、m>1 B、m<2 C、1<m<2 D、1<m≤210. 如图,牧童在A处牧马,牧童的家在B处,A , B处到河岸的距离分别是AC=300m,BD=500m,且C , D两地之间的距离为600m.牧童从A处将马牵到河边去饮水,再牵回家,他至少要走的路程是( ) A、1400m B、m C、1000m D、m
A、1400m B、m C、1000m D、m二、填空题
-
11. 函数自变量x的取值范围是.12. 如图,在△ABC中,∠ACB=90°,CE是△ABC的角平分线,∠AEC=105°,则∠B=°.
 13. 在平面直角坐标系中,将点A(a , 1)先向右平移3个单位,再向下平移2个单位,得到点B(5,b),则ab的值为.14. 某批电子产品进价为300元/件,售价为400元/件.为提高销量,商店准备将这批电子产品降价出售,若要保证单件利润率不低于20%,则最多可降价元.15. 《九章算术》有一问题∶“今有垣高一丈,倚木于垣,上与垣齐.引木却行一尺,其木至地.问木长几何?”其内容可表述为∶“有一面墙,高1丈.将一根木杆斜靠在墙上,使木杆的上端与墙的上端对齐,下端落在地面上,如果使木杆下端从此时的位置向远离墙的方向移动1尺,则木杆上端恰好沿着墙滑落到地面上,则木杆长为尺.”(说明:1丈=10尺)16. 如图,在平面直角坐标系中,一次函数y=-2x+4的图象与x轴、y轴分别交于点A和点B , 过点B的直线BC:y=kx+b交x轴于点C(-8,0).
13. 在平面直角坐标系中,将点A(a , 1)先向右平移3个单位,再向下平移2个单位,得到点B(5,b),则ab的值为.14. 某批电子产品进价为300元/件,售价为400元/件.为提高销量,商店准备将这批电子产品降价出售,若要保证单件利润率不低于20%,则最多可降价元.15. 《九章算术》有一问题∶“今有垣高一丈,倚木于垣,上与垣齐.引木却行一尺,其木至地.问木长几何?”其内容可表述为∶“有一面墙,高1丈.将一根木杆斜靠在墙上,使木杆的上端与墙的上端对齐,下端落在地面上,如果使木杆下端从此时的位置向远离墙的方向移动1尺,则木杆上端恰好沿着墙滑落到地面上,则木杆长为尺.”(说明:1丈=10尺)16. 如图,在平面直角坐标系中,一次函数y=-2x+4的图象与x轴、y轴分别交于点A和点B , 过点B的直线BC:y=kx+b交x轴于点C(-8,0). (1)、k的值为;(2)、点M为直线BC上一点,若∠MAB=∠ABO , 则点M的坐标是.
(1)、k的值为;(2)、点M为直线BC上一点,若∠MAB=∠ABO , 则点M的坐标是.三、解答题
-
17. 解不等式组 , 并把解表示在数轴上.18. 如图,∠D=∠ACB=∠E=90°,AC=BC.求证:△ADC≌△CEB.
 19. 已知点A(2,2),B(-2,2), C(2,-3).
19. 已知点A(2,2),B(-2,2), C(2,-3). (1)、在平面直角坐标系中画出点A , B , C , 判断A , B两点连线与y轴的位置关系;(2)、已知点D(-3,m),若CDx轴,求m的值.20. 某公交车司机统计了月乘车人数x(人)与月利润y(元)的部分数据如下表,假设每位乘客的公交票价固定不变,公交车月支出费用为6000元.(月利润=月收入-月支出费用)
(1)、在平面直角坐标系中画出点A , B , C , 判断A , B两点连线与y轴的位置关系;(2)、已知点D(-3,m),若CDx轴,求m的值.20. 某公交车司机统计了月乘车人数x(人)与月利润y(元)的部分数据如下表,假设每位乘客的公交票价固定不变,公交车月支出费用为6000元.(月利润=月收入-月支出费用)x(人)
…
2500
2750
3000
3500
4000
…
y(元)
…
-1000
-500
0
1000
2000
…
(1)、根据函数的定义,y是关于x的函数吗?(2)、结合表格解答下列问题:①公交车票的单价是多少元?
②当x=2750时,y的值是多少?它的实际意义是什么?
21. 已知:如图,在△ABC中,∠B=30°,∠ACB=45°,AD是BC边上的高线,CE是AB边上的中线. (1)、求证:AE=CD;(2)、求∠ACE的度数.22. 已知一次函数y=kx+b(k≠0)的图象过点(0,1).(1)、若函数图象还经过点(-1,3),
(1)、求证:AE=CD;(2)、求∠ACE的度数.22. 已知一次函数y=kx+b(k≠0)的图象过点(0,1).(1)、若函数图象还经过点(-1,3),①求这个函数的表达式;
②若点P(a , a+3)关于x轴的对称点恰好落在该函数的图象上,求a的值.
(2)、若函数图象与x轴的交点的横坐标满足2<<3,求k的取值范围.23. 项目研究:剪等腰三角形 (1)、动手尝试:
(1)、动手尝试:如图,有甲,乙两张三角形纸片,甲三角形纸片的内角分别为40°,60°,80°;乙三角形纸片的内角分别为35°,40°,105°,你能把每一张三角形纸片剪成两个等腰三角形吗?若能,请画出剪痕并标出各角的度数;若不能,请说明理由.
(2)、项目研究:结合上述尝试,请思考归纳出一张三角形纸片能剪成两个等腰三角形需具备的条件,并画出相应的示意图说明剪法.
24. 已知,一次函数y=x+4的图象与x轴、y轴分别交于点A , 点B , 点C的坐标为(-2,0). (1)、求点A , 点B的坐标;(2)、过点C作直线CD , 与AB交于点D , 且 , 求点D的坐标;(3)、连接BC , 将△OBC沿x轴向左平移得到△O′B′C′ , 再将以A , B , B′ , C′为顶点的四边形沿O′B′剪开得到两个图形.若用这两个图形拼成不重叠且无缝隙的图形恰好是三角形,求△OBC平移的距离.
(1)、求点A , 点B的坐标;(2)、过点C作直线CD , 与AB交于点D , 且 , 求点D的坐标;(3)、连接BC , 将△OBC沿x轴向左平移得到△O′B′C′ , 再将以A , B , B′ , C′为顶点的四边形沿O′B′剪开得到两个图形.若用这两个图形拼成不重叠且无缝隙的图形恰好是三角形,求△OBC平移的距离.