四川省绵阳市游仙区2022-2023学年八年级上学期期中数学试题

试卷更新日期：2022-11-16 类型：期中考试

进入出卷网下载

一、单选题

1. 三角形是指（）

A、由三条线段所组成的封闭图形 B、由不在同一直线上的三条直线首尾顺次相接组成的图形 C、由不在同一直线上的三条线段首尾顺次相接组成的图形 D、由三条线段首尾顺次相接组成的图形

查看试题解析
2. 下列说法不正确的是（）

A、两条直角边对应相等的两个直角三角形全等 B、一锐角和斜边对应相等的两个直角三角形全等 C、斜边和一直角边对应相等的两个直角三角形全等 D、有两边相等的两个直角三角形全等

查看试题解析
3. 设三角形三边之长分别为6，a，2，则a的值可能为（）

A、6 B、4 C、8 D、3

查看试题解析
4. 如图，在△ABC中，AD⊥AB，有下列三个结论：①AD是△ACD的高；②AD是△ABD的高；③AD是△ABC的高．其中正确的结论是（）

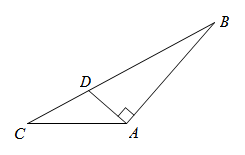A、①和② B、①和③ C、②和③ D、只有②正确

查看试题解析
5. 如下图， $∠ A = 70 °$ ， BP、CP分别平分∠ABC和∠ACB，则∠P的度数是（）

A、125° B、115° C、110° D、35°

查看试题解析
6. 在△ABC中，∠B＝60°，AD是△ABC的角平分线，∠DAC＝31°，则∠C的度数为（）

A、62° B、60° C、92° D、58°

查看试题解析
7. 如图，直线a//b，Rt△ABC 如图放置，若∠1=28°，∠2=80°，则∠B的度数为（）

A、62° B、52° C、38° D、28°

查看试题解析
8. 如图，在正五边形 $A B C D E$ 中，连接 $A D$ ，则 $∠ 1$ 的度数为（）

A、 $30 °$ B、 $36 °$ C、 $45 °$ D、 $72 °$

查看试题解析
9. 如图， $△ A B C ≌ △ A E D$ ，点E在线段BC上， $∠ 1 = 56 °$ ，则 $∠ A E D$ 的大小为（）

A、34° B、56° C、62° D、68°

查看试题解析
10. 如图，在 $△ A B C$ 中， $∠ B = ∠ C$ ， M，N，P分别是边AB，AC，BC上的点，且 $B M = C P$ ， $C N = B P$ ，若 $∠ M P N = 44 °$ ，则 $∠ A$ 的度数为（）

A、 $44 °$ B、 $88 °$ C、 $92 °$ D、 $136 °$

查看试题解析
11. 如图，在△ABC中，AD是高，AE是角平分线，AF是中线．则下列结论错误的是（）

A、BF＝CF B、∠BAF＝∠CAF C、∠B＋∠BAD＝90° D、 $S_{△ A B C} = 2 S_{△ A B F}$

查看试题解析
12. 下列各式中，计算正确的是（）

A、 $7 a - 3 b = 4 a b$ B、 ${(a^{2})}^{3} = a^{5}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 $a^{3} \cdot a = a^{4}$

查看试题解析
13. 下列各式中，计算正确的是（）

A、 $x^{2} + 2 x^{2} = - 2 x^{4}$ B、 ${(3 x^{2} y^{3})}^{2} = 6 x^{4} y^{6}$ C、 ${(- x^{3})}^{3} = - x^{9}$ D、 $x^{2} (x - 1) = x^{3} - 1$

查看试题解析
14. 下列式子中，能用平方差公式运算的是（）

A、 $(- x + y) (y - x)$ B、 $(x + y) (- x - y)$ C、 $(- y + x) (x + y)$ D、 $(x - y) (- x + y)$

查看试题解析
15. 如图有三种不同的纸片，现选取4张拼成了图甲，你能根据面积关系得到下列等式成立的是（）

A、 $a (a + b) = a^{2} + a b$ B、 $a^{2} - b^{2} = (a + b) (a - b)$ C、 ${(a - b)}^{2} = a^{2} - 2 a b + b^{2}$ D、 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$

查看试题解析

二、填空题

16. 已知，三角形的三边长为3，5，m，则m的取值范围是．

查看试题解析
17. 如果等式 ${(a - 1)}^{a + 2} = 1$ ，那么 $a$ 的值为．

查看试题解析
18. 若 $(x + 3) \cdot (x - p) = x^{2} + m x - 27$ ，则 $m + p$ 的值是．

查看试题解析
19. 已知一个长方形的面积是 $4 x^{2} + 2 x$ ，宽为 $2 x$ ，那么它的长为．

查看试题解析
20. 如图，∠2∶∠3∶∠4＝3∶9∶7，则∠1＝°．

查看试题解析
21. 如图，△ABC≌△ADE，AB=8，AC=5，BC=6，则CD= ．

查看试题解析
22. 如图， $∠ D A C = 2 x ， ∠ A C B = 4 x ， ∠ A B C = 3 x ， A D = B C$ ，则 $∠ B A D =$ ．

查看试题解析
23. 如图，在 $Rt Δ A B C$ 中， $∠ C = 90 °$ ， $A D$ 平分 $∠ B A C$ 交 $B C$ 于点 $D$ ．若 $B D ： C D = 3 ： 2$ ，点 $D$ 到 $A B$ 的距离是8，则 $B C$ 的长是．

查看试题解析
24. 一个正方形的边长增加2cm，其面积会增加 $32 {cm}^{2}$ ，则这个正方形的面积是 ${cm}^{2}$ ．

查看试题解析
25. 某工厂原来生产一种边长为a厘米的正方形地砖，现将地砖的一边扩大3厘米，另一边缩短3厘米，改成生产长方形地砖．若材料的成本价为每平方厘米b元，则这种长方形地砖每块的材料成本价与正方形地砖相比减少了元．

查看试题解析

三、解答题

26.

(1)、已知 $a^{m} = 3$ ， $a^{n} = 4$ ，求 $a^{2 m + 3 n}$ 的值；

(2)、已知 $9^{n + 1} - 3^{2 n} = 72$ ，求 $n$ 的值．

查看试题解析
27. 如图，在Rt△ABC中，∠ACB＝90°，∠A＝36°，△ABC的外角∠CBD的平分线BE交AC的延长线于点E，F为AC延长线上的一点，连接DF．

(1)、求∠CBE的度数．

(2)、若∠F＝27°，求证：BE $∥$ DF．

查看试题解析
28. 用10块高度相同长方体小木块垒了两堵与地面垂直的木墙 $A D$ 、 $B E$ ， $A D = 9 c m$ ， $B E = 21 c m$ ，两木墙之间刚好可以放进一个等腰直角三角板 $(A C = B C ， ∠ A C B = 90 °)$ ，点C在 $D E$ 上，点A和B分别与木墙的顶端重合，求两堵木墙之间的距离．

查看试题解析
29. 如图，在 $△ A B C$ 中， $A D$ 是角平分线，点E是边 $A C$ 上一点，且满足 $∠ A D E = ∠ B ， A E = 3$ ， $A D = 5$ ，求 $A B$ 的长．

查看试题解析
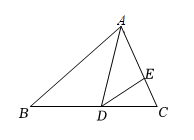30. 如图，某中学校园内有一块长为（3a+2b）米，宽为（2a+b）米的长方形地块，学校计划在中间留一块长为（2a-b）米、宽为2b米的小长方形地块修建一座雕像，然后将阴影部分进行绿化．

(1)、求长方形地块的面积；（用含a，b的代数式表示）

(2)、求修建雕像的小长方形地块的面积；（用含a，b的代数式表示）

(3)、当a＝3，b＝1时，求绿化部分的面积．

查看试题解析
31. 课本再现

(1)、在课本11.2.2章节中，我们学习了三角形内角和定理得出的推论：三角形的外角等于与它不相邻的两个内角的和．
已知： $∠ A C D$ 是 $△ A B C$ 的一个外角（如图1）．求证： $∠ A C D = ∠ A + ∠ B$ ．

证明：如图2，过点C作 $C E ∥ A B$ ．（请完成后面的证明）

(2)、如图3，线段 $A B ， C D$ 相交于点O，连接 $A C ， B D$ ，我们把形如这样的图形称为“8字型”．请仔细观察该图形，直接写出 $∠ A ， ∠ B ， ∠ C ， ∠ D$ 之间的数量关系．

(3)、如图4，由线段组成的一个“风筝”形状，运用（2）中得出的数量关系，解答下列问题．
①试比较 $∠ B + ∠ C$ 与 $∠ A + ∠ D + ∠ E + ∠ F$ 的大小，并说明理由；

②若 $∠ B O F = 120 °$ ，则 $∠ A + ∠ B + ∠ C + ∠ D + ∠ E + ∠ F =$ ▲ ．

查看试题解析