湖南省长沙市长郡教育集团2022-2023学年八年级上学期期中考试数学试题

试卷更新日期：2022-11-16 类型：期中考试

进入出卷网下载

一、单选题

1. “致中和，天地位焉，万物育焉．”对称美是我国古人和谐平衡思想的体现，常被运用于建筑、器物、绘画、标识等作品的设计上，使对称之美惊艳了千年的时光．下列大学的校徽图案是轴对称图形的是（）

A、清华大学 B、北京大学 C、中国人民大学 D、浙江大学

查看试题解析
2. 若一个三角形的两边长分别为3 $cm$ 、6 $cm$ ，则它的第三边的长可能是（）

A、2 $cm$ B、3 $cm$ C、6 $cm$ D、9 $cm$

查看试题解析
3. 下列各式计算正确的是（）

A、 $a^{2} \cdot a^{4} = a^{8}$ B、 ${(2 x y)}^{3} = 6 x^{3} y^{3}$ C、 $a^{6} \div a^{3} = a^{2}$ D、 ${(- a^{3})}^{2} = a^{6}$

查看试题解析
4. 下列图形中，具有稳定性的是（）

A、 B、 C、 D、

查看试题解析
5. 如图是两个全等三角形，图中的字母表示三角形的边长，则 $∠ 1$ 的度数是（）

A、54° B、56° C、60° D、66°

查看试题解析
6. 如图，在等腰 $Δ A B C$ 中， $A B = A C$ ， $∠ A = 40 °$ ， BD是 $∠ A B C$ 的角平分线，则 $∠ A D B$ 的度数等于（）

A、 $70 °$ B、 $100 °$ C、 $105 °$ D、 $120 °$

查看试题解析
7. 如果（2x+m）与（x+3）的乘积中不含x的一次项，那么m的值为（）

A、-6 B、-3 C、0 D、1

查看试题解析
8. 一个多边形的内角和等于外角和的两倍，那么这个多边形是（）

A、三边形 B、四边形 C、五边形 D、六边形

查看试题解析
9. 如图，在等边△ABC中，BD平分∠ABC交AC于点D，过点D作DE⊥BC于点E，且CE=1.5，则AB的长为（）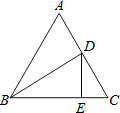

A、3 B、4.5 C、6 D、7.5

查看试题解析
10. 如图，在△ABC中，AB＝8cm，BC＝6cm，AC＝5cm.沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD，则△AED 的周长是（）

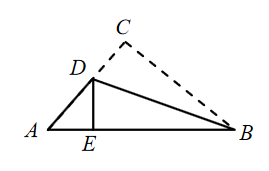A、5cm B、6cm C、7cm D、8cm

查看试题解析
11. 下面四个整式中，不能表示图中阴影部分面积的是（）

A、 $(x + 3) (x + 2) - 2 x$ B、 $x (x + 3) + 6$ C、 $3 (x + 2) + x^{2}$ D、 $x^{2} + 5 x$

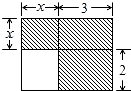查看试题解析
12. 已知a，b，c分别是等腰△ABC三边的长，且满足ac＝12-bc，若a，b，c均为正整数，则这样的等腰△ABC存在（）

A、3个 B、4个 C、5个 D、6个

查看试题解析

二、填空题

13. ${(π - 2)}^{0} =$ ．

查看试题解析
14. 如图，已知 $A B ⊥ B D$ ， $A B ∥ E D$ ， $A B = E D$ ，要说明 $△ A B C ≌ △ E D C$ ，可补充的一个条件为(答案不唯一，写一个即可).

查看试题解析
15. 用直尺和圆规作一个角等于已知角，如图，能得出 $∠ A^{'} O^{'} B^{'} = ∠ A O B$ 的依据是全等三角形判定定理中的．

查看试题解析
16. 如图所示的正方形的方格中，∠1＋∠3-∠2＝度．

查看试题解析
17. 如图，在△ABC中，CD是它的角平分线，DE⊥AC于点 E.若BC＝6cm，DE＝2cm，则△BCD的面积为cm²

查看试题解析
18. 如图，△ABC为等边三角形，点D与点C关于直线AB对称，E，F分别是边BC和AC上的点，BE＝CF，AE与BF交于点G．DG交AB于点H．下列四个结论中：①△ABE≌△BCF；②AG+BG＝DG；③HG+GE＝GF；④△AHF为等边三角形．所有正确结论的序号是．

查看试题解析

三、解答题

19. 计算：

(1)、 $a^{2} \cdot {(- a^{4})}^{3} \div {(a^{3})}^{2}$ ；

(2)、 $(2 x + y) (x - y) - 2 (y^{2} - x y)$ ．

查看试题解析
20. 如图，在平面直角坐标系 $x O y$ 中，△ABC的顶点都在网格线的交点上，点B的坐标为 $(- 2 ， 0)$ ，点C的坐标为 $(- 1 ， 2)$ ．

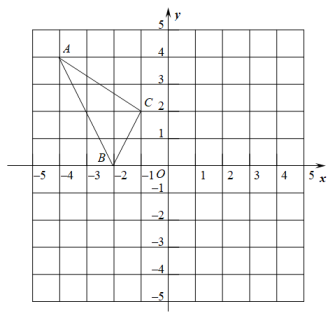(1)、直接写出点A的坐标和点A关于y轴的对称点的坐标，并画出 $△ A B C$ 关于y轴的对称图形 $△ A_{1} B_{1} C_{1}$ ；（不写画法，保留画图痕迹）

(2)、求 $△ A_{1} B_{1} C_{1}$ 的面积．

查看试题解析
21. 先化简，再求值： $x (2 x^{2} - 4 x) - x^{2} (6 x - 3) + x {(2 x)}^{2}$ ，其中 $x = - \frac{1}{2}$ ．

查看试题解析
22. 如图，AB∥CD，AE⊥BD，CF⊥BD，垂足分别是E、F，且BF=DE，求证：AE=CF

查看试题解析
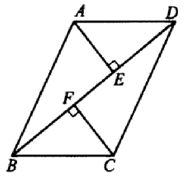23. 如图，AB＝AC，∠BAC＝120°，AB的垂直平分线交BC于点D．

(1)、求∠ADC的度数；

(2)、求证：DC＝2DB．

查看试题解析
24. 如图，点C，E，F，B在同一直线上，点A，D在BC异侧，AB∥CD，AE＝DF，∠A＝∠D．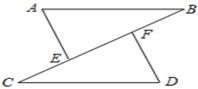

(1)、求证：AB＝CD；

(2)、若AB＝CF，∠B＝40°，求∠D的度数．

查看试题解析
25. 如图，在Rt△ABC中，∠ACB＝90，∠A＝30°，AC＝ $6 \sqrt{3}$ ， BC＝6，CD平分∠ACB交斜边AB于点D，动点P从点C出发，沿折线CA―AD向终点D运动．

(1)、点P在CA上运动的过程中，当CP＝时，△CPD与△CBD的面积相等；（直接写出答案）

(2)、点P在折线CA―AD上运动的过程中，若△CPD是等腰三角形，求∠CPD的度数；

(3)、若点E是斜边AB的中点，当动点P在CA上运动时，线段CD所在直线上存在另一动点M，使两线段MP、ME的长度之和，即MP＋ME的值最小，则此时CP的长度＝．（直接写出答案）

查看试题解析
26. 规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．
从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．

(1)、如图1，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ ，请写出图中两对“等角三角形”；

(2)、如图2，在 $△ A B C$ 中， $C D$ 为 $∠ A C B$ 的平分线， $∠ A = 40 °$ ， $∠ B =60 °$ ．求证： $C D$ 为 $△ A B C$ 的“等角分割线”；

(3)、在 $△ A B C$ 中，若 $∠ A = 50 °$ ， $C D$ 是 $△ A B C$ 的“等角分割线”，请求出所有可能的 $∠ A C B$ 的度数．

查看试题解析