浙江省舟山市普陀区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-11-16 类型:期末考试
一、单选题
-
1. 根据下列已知条件,能画出唯一的的是( )A、 , B、 , , C、 , , D、 , ,2. 如图,下列图案是我国几家银行的标志,其中轴对称的图形有( )



 A、1个 B、2个 C、3个 D、4个3. 下列句子属于命题的是( ).A、正数大于一切负数吗? B、钝角大于直角 C、将 开平方 D、作线段 的中点4. 如图,△ABC中,AB=AC,过点A作DA⊥AC交BC于点D.若∠B=2∠BAD,则∠BAD的度数为( )
A、1个 B、2个 C、3个 D、4个3. 下列句子属于命题的是( ).A、正数大于一切负数吗? B、钝角大于直角 C、将 开平方 D、作线段 的中点4. 如图,△ABC中,AB=AC,过点A作DA⊥AC交BC于点D.若∠B=2∠BAD,则∠BAD的度数为( ) A、18° B、20° C、30° D、36°5. 如图,直线a∥b,AC⊥AB于A,AC交直线b于点C,∠1=50°,则∠2的度数是( )
A、18° B、20° C、30° D、36°5. 如图,直线a∥b,AC⊥AB于A,AC交直线b于点C,∠1=50°,则∠2的度数是( ) A、50° B、40° C、25° D、20°6. 不等式组 的解集在数轴上的表示是( )A、
A、50° B、40° C、25° D、20°6. 不等式组 的解集在数轴上的表示是( )A、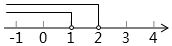 B、
B、 C、
C、 D、
D、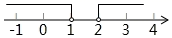 7. 已知点在直线上,则k的值为( )A、 B、 C、4 D、8. 在平面直角坐标系中,点 关于 轴对称的点的坐标是( )A、 B、 C、 D、9. 如图是两个全等的三角形纸片,其三边长之比为 , 按图中方法分别将其对折,使折痕(图中虚线)过其中的一个顶点,且使该顶点所在两边重合,记折叠后不重叠部分面积分别为 , 已知 , 则纸片的面积是( )
7. 已知点在直线上,则k的值为( )A、 B、 C、4 D、8. 在平面直角坐标系中,点 关于 轴对称的点的坐标是( )A、 B、 C、 D、9. 如图是两个全等的三角形纸片,其三边长之比为 , 按图中方法分别将其对折,使折痕(图中虚线)过其中的一个顶点,且使该顶点所在两边重合,记折叠后不重叠部分面积分别为 , 已知 , 则纸片的面积是( ) A、102 B、104 C、106 D、10810. 如图,等腰 的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让 沿这条直线向右平移,直到点A与点E重合为止 设CD的长为x , 与正方形DEFG重合部分 图中阴影部分 的面积为y , 则y与x之间的函数关系的图象大致是( )
A、102 B、104 C、106 D、10810. 如图,等腰 的直角边与正方形DEFG的边长均为2,且AC与DE在同一直线上,开始时点C与点D重合,让 沿这条直线向右平移,直到点A与点E重合为止 设CD的长为x , 与正方形DEFG重合部分 图中阴影部分 的面积为y , 则y与x之间的函数关系的图象大致是( )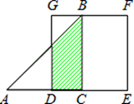 A、
A、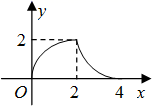 B、
B、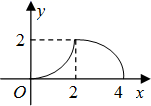 C、
C、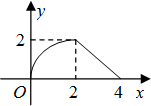 D、
D、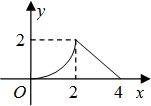
二、填空题
-
11. 已知 , 且 , 设 , 则m的取值范围是.12. 如图,已知等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则∠EFD= .
 13. 如图,如果●的位置是(2,3),◆的位置为(1,1),那么★的位置可表示为.
13. 如图,如果●的位置是(2,3),◆的位置为(1,1),那么★的位置可表示为. 14. 已知一次函数的图像经过点、、则.15. 已知中, , , , 以三边分别向外作三个正方形,连接各点,得到六边形DEFGHI,则六边形DEFGHI的面积为.
14. 已知一次函数的图像经过点、、则.15. 已知中, , , , 以三边分别向外作三个正方形,连接各点,得到六边形DEFGHI,则六边形DEFGHI的面积为. 16. 如图,在平面直角坐标系 中, 为坐标原点, ,点 在 轴上运动,以 为边作等腰 , (点 , , 呈顺时针排列),当点 在 轴上运动时,点 也随之运动.在点 的运动过程中, 的最小值为.
16. 如图,在平面直角坐标系 中, 为坐标原点, ,点 在 轴上运动,以 为边作等腰 , (点 , , 呈顺时针排列),当点 在 轴上运动时,点 也随之运动.在点 的运动过程中, 的最小值为.
三、解答题
-
17. 解不等式组:18. 在中, , 是射线上一点,点在的右侧,线段 , 且 , 连结.
 (1)、如图1,点在线段上,求证:.(2)、如图2,点在线段延长线上,判断与的数量关系并说明理由.19. 如图,平面直角坐标系中,的顶点坐标为:
(1)、如图1,点在线段上,求证:.(2)、如图2,点在线段延长线上,判断与的数量关系并说明理由.19. 如图,平面直角坐标系中,的顶点坐标为: (1)、将向左平移5个单位长度,再向下平移2个单位长度,得.画出 , 并写出的顶点坐标:(2)、求的面积.20. 如图,在平面直角坐标系中,直线l1:y x+1交y轴于点A,直线l2:y x+t分别交y轴,x轴,直线l1于点B,C,D.
(1)、将向左平移5个单位长度,再向下平移2个单位长度,得.画出 , 并写出的顶点坐标:(2)、求的面积.20. 如图,在平面直角坐标系中,直线l1:y x+1交y轴于点A,直线l2:y x+t分别交y轴,x轴,直线l1于点B,C,D. (1)、求点A的坐标,并用含t的代数式表示B,C,D的坐标;(2)、当t>0时,若S△OBC=S△OBD , 求t的值;(3)、P是x轴上的一点,连结AP,DP,若AP=DP,且∠APD=90°,求t的值.21. 如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC.
(1)、求点A的坐标,并用含t的代数式表示B,C,D的坐标;(2)、当t>0时,若S△OBC=S△OBD , 求t的值;(3)、P是x轴上的一点,连结AP,DP,若AP=DP,且∠APD=90°,求t的值.21. 如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC. (1)、求证:△ABE≌△CBD;(2)、若∠CAE=30°,求∠BDC的度数.22. 已知用2辆A型车和1辆B型车装满货物一次可运货11吨;用3辆A型车和2辆B型车装满货物一次可运货19吨,某物流公司现有50吨货物,计划同时租用A型车a辆,B型车b辆,一次运转,且恰好每辆车都装满货物.
(1)、求证:△ABE≌△CBD;(2)、若∠CAE=30°,求∠BDC的度数.22. 已知用2辆A型车和1辆B型车装满货物一次可运货11吨;用3辆A型车和2辆B型车装满货物一次可运货19吨,某物流公司现有50吨货物,计划同时租用A型车a辆,B型车b辆,一次运转,且恰好每辆车都装满货物.根据以上信息,解答下列问题:
(1)、1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?(2)、请你帮该物流公司设计,有几种租车方案?(3)、若A型车每辆需租金100元/次,B型车每辆需租金120元次,请选出最省钱的租车方案,并求出最少租车费.23. 如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边顺时针运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.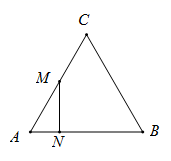 (1)、点M、N运动几秒后,M、N两点重合?(2)、点M、N运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间;(3)、点M、N运动几秒后,可得到直角三角形△AMN?24. 如图,在平面直角坐标系中, , 将线段平移至线段 , 点C在y轴的正半轴上,点D在第一象限内,连接.
(1)、点M、N运动几秒后,M、N两点重合?(2)、点M、N运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间;(3)、点M、N运动几秒后,可得到直角三角形△AMN?24. 如图,在平面直角坐标系中, , 将线段平移至线段 , 点C在y轴的正半轴上,点D在第一象限内,连接. (1)、直接写出图中平行的线段,用“//”表示:;(2)、设点 , 则点D的坐标可表示为;(3)、求出点C,D的坐标;(4)、如图,过点D作x轴的平行线a,点P从点D出发,以每秒1个单位长度的速度沿直线a向左移动,同时,点Q从点A出发,以每秒2个单位长度的速度沿x轴向右移动.
(1)、直接写出图中平行的线段,用“//”表示:;(2)、设点 , 则点D的坐标可表示为;(3)、求出点C,D的坐标;(4)、如图,过点D作x轴的平行线a,点P从点D出发,以每秒1个单位长度的速度沿直线a向左移动,同时,点Q从点A出发,以每秒2个单位长度的速度沿x轴向右移动.①求经过几秒钟后,以Q、O、D、P为顶点的四边形面积;
②在①的条件下,若交y轴于点M,请直接写出点M的坐标.