浙江省舟山市定海区2021-2022学年八年级上学期期末数学试题
试卷更新日期：2022-11-16 类型：期末考试
一、单选题
-
1. 下列四个数学符号中，是轴对称图形的是（ ）A、 B、 C、 D、2. 如图，△ABC中AC边上的高是哪条垂线段.（ ）
A、AE B、CD C、BF D、AF3. 在△ABC中，已知AB=3，BC=4，则AC的长可能是（ ）A、1 B、4 C、7 D、94. 下列选项中a的值，可以作为命题“则”是假命题的反例是（ ）A、 B、 C、 D、5. 将点A向左平移3个单位，再向上平移4个单位得到点B，则点B的坐标是（ ）A、（-5，-7） B、（-5，1） C、（1，1） D、（1，-7）6. 在某一阶段，某商品的销售量与销售价之间存在如下关系：销售价/元
90
100
110
120
130
140
销售量/件
90
80
70
60
50
40
设该商品的销售价为x元，销售量为y件，估计当x=127时，y的值为（ ）
A、63 B、59 C、53 D、437. 关于一次函数y=3x-1的描述，下列说法正确的是（ ）A、图象经过第一、二、三象限 B、函数的图象与x轴的交点是（0，-1） C、向下平移1个单位，可得到y=3x D、图象经过点（1，2）8. 如图，在Rt∆ ABC中，∠B＝90°，作AC的中垂线l交BC于点D，连接AD，若AB＝3，BC＝9，则BD的长为（ ）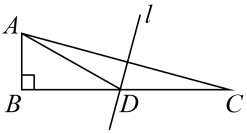
A、6 B、5 C、4 D、39. 对于任意实数p、q，定义一种运算：p@q＝p-q＋pq，例如2@3＝2-3＋2×3.请根据上述定义解决问题：若关于x的不等式组有3个整数解，则m的取值范围为是 （ ）A、-8≤m<-5 B、-8<m≤-5 C、-8≤m≤-5 D、-8<m<-510. 如图，在等腰中， ， ， 于点D，点P是延长线上一点，点O在延长线上， ， 下面的结论：①；②是正三角形；③；④ ， 其中正确的个数是（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
11. “x的5倍与y的差大于1”用不等式表示为.12. 点P（2，3）关于x轴的对称点的坐标为 ．13. 命题“等腰三角形的两个底角相等”的逆命题是 ， 它是命题（填“真”或“假”）14. 如图，直线mn，以直线m上的点A为圆心，适当长为半径画弧，分别交直线m，n于点B、C，连接AC、BC，若∠1＝30°，则∠2＝.
15. 在边长为1的网格图形中，以顶点都是格点的正方形ABCD的边为斜边，向外作四个全等的直角三角形，使四个直角顶点E，F，G，H都是格点，且四边形EFGH为正方形，在图1所示的格点图形中，正方形ABCD的边长为 ， 此时正方形EFGH的面积为52.写出正方形EFGH的面积的所有可能值是（不包括52）.
16. 在平面直角坐标系中，A（2，0），B（0，4），过点B作直线lx轴，点P（a，4）是线l上的动点，以AP为边在AP右侧作等腰Rt∆APQ，使∠APQ＝90°.
(1)、当a＝0时，则点Q的坐标是.(2)、当点P在直线1上运动时，点Q也随之运动，则OQ的最小值是.三、解答题
-
17. 解不等式组 ， 并把解集在数轴上表示出来.
18. 有一张图纸被损坏，但上面有如图的两个标志点A（-3，1），B（-3，-3）可认，而主要建筑C（3，2）破损.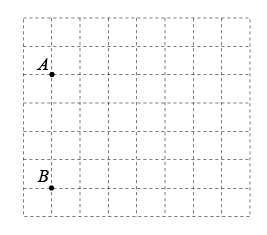
(1)、建立直角坐标系；(2)、标出图中C点的位置；(3)、求出线段AC的长.19. 如图，已知在四边形ABCD中，ADBC，∠A＝90°，AD＝BE，CE⊥BD，垂足为E.
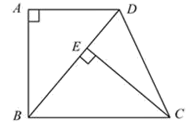(1)、求证：BD＝BC；(2)、若∠DBC＝50°，求∠DCE的度数.20. 如图，直线y=kx+b经过点A（-5，0），B（-1，4）
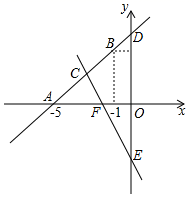(1)、求直线AB的表达式；(2)、求直线CE：y=-2x-4与直线AB及y轴围成图形的面积；(3)、根据图象，直接写出关于x的不等式kx+b＞-2x-4的解集.21. 为响应舟山市创建全国文明城市，某校决定安装垃圾分类的温馨提示牌和垃圾箱，若购买2个温馨提示牌和3个垃圾箱共需550元，且垃圾箱的单价是温馨提示牌单价的3倍.(1)、购买1个温馨提示牌和1个垃圾箱各需多少元？(2)、如果需要购买温馨提示牌和垃圾箱共100个，费用不超过8000元，问：最多购买垃圾箱多少个？22. 小玲和小东姐弟俩分别从家和图书馆同时出发，沿同一条路相向而行，小玲开始跑步中途改为步行，到达图书馆恰好用30分钟.小东骑自行车以300米/分钟的速度直接回家，两人离家的路程y（米）与各自离开出发地的时间x（分钟）之间的函数图象，如图所示：
(1)、家与图书馆之间的路程为多少米？小玲步行的速度为多少？(2)、求小东离家的路程y关于x的函数解析式，并写出自变量的取值范围；(3)、当两人相遇时，他们离图书馆多远？23. 如果有两点到一条直线的距离相等，那么称这条直线为“两点的等距线”.
(1)、如图1，直线CD经过线段AB的中点P，试说明直线CD是点A、B的一条等距线.(2)、如图2，A、B、C是正方形网格中的三个格点，请在网格中作出所有的直线m，使直线m过点C且直线m是“A、B的等距线”.(3)、如图3，∆ABC中，A（1，-2），B（4，-1），C（2，-0.5）.坐标轴上是否存在点P，使S∆APC＝S∆BPC，若存在，求出点P的坐标；若不存在，请说明理由.24.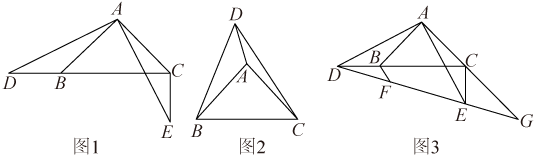
（1）如图1，在Rt∆ABC中，AB＝AC，D是直线BC上的一点，将线段AD绕点A逆时针旋转90°至AE，连接CE，求证：∆ABD≌∆ACE； (1)、如图2，A是∆BDC内一点，∠ABC＝∠ADB＝45°，∠BAC＝90°，BD＝6，线段AD绕点A逆时针旋转90°至AE，点D、E、B恰好共线，求∆BDC的面积；(2)、如图3，在图1的条件下，延长DE，AC交于点G，BF⊥AB交DE于点F，求证：FG＝AE.