浙江省温州市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列冬奥会会徽中，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若三角形两边长分别为7 cm和10 cm，则第三边长可能为（）

A、2 cm B、3 cm C、8 cm D、17 cm

查看试题解析
3. 不等式 $3 x > 6$ 的解为（）

A、 $x > \frac{1}{2}$ B、 $x < \frac{1}{2}$ C、 $x > 2$ D、 $x < 2$

查看试题解析
4. 下列选项中各坐标对应的点，落在如图所示平面直角坐标系阴影区域内的是（）

A、 $(1 ， 2)$ B、 $(2 ， 0)$ C、 $(0 ， 3)$ D、 $(- 1 ， - 1)$

查看试题解析
5. 能说明命题“如果a是任意实数，那么 $\sqrt{a^{2}} = a$ ”是假命题的反例是（）

A、 $a = - 1$ B、 $a = 0$ C、 $a = \sqrt{2}$ D、 $a = 2$

查看试题解析
6. 如图，△ABC≌△DEF，点A，B分别对应点D，E.若∠A=70°，∠B=50°，则∠1等于（）

A、50° B、60° C、70° D、80°

查看试题解析
7. 在平面直角坐标系中，有四个点 $A (4 ， 8)$ ， $B (4 ， 2)$ ， $C (2 ， 4)$ ， $D (- 1 ， - 2)$ ，其中不在同一正比例函数图象上的是（）

A、点A B、点B C、点C D、点D

查看试题解析
8. 如图，已知线段AB，以点A，B为圆心，5为半径作弧相交于点C，D.连结CD，点E在CD上，连结CA，CB，EA，EB.若 $△ A B C$ 与 $△ A B E$ 的周长之差为4，则AE的长为（）

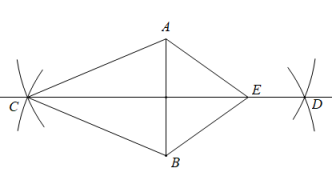A、1 B、2 C、3 D、4

查看试题解析
9. 已知A，B两地相距1680米，甲步行沿一条笔直的公路从A地出发到B地.乙骑自行车比甲晚7分钟从B地出发，沿同一条公路到达A地后立刻以原速度返回，并与甲同时到达B地.甲、乙离A地的距离y（米）与甲行走时间x（分）的函数图象如图所示，则甲出发后两人第一次相遇所需的时间是（）

A、10分钟 B、10.5分钟 C、11分钟 D、11.5分钟

查看试题解析
10. 在活动课上，同学们用4张图1所示的纸片拼出了两个不同的六边形（图2，图3中的空白部分），将两个六边形分割，图形Ⅰ，Ⅱ均为正方形.已知 $B C = \sqrt{10}$ ， $A C = \sqrt{2}$ ，则CD等于（）

A、 $\sqrt{20}$ B、 $\sqrt{23}$ C、5 D、 $\sqrt{26}$

查看试题解析

二、填空题

11. “a的一半与3的和小于-2”用不等式表示为.

查看试题解析
12. 在平面直角坐标系中，点（-1，2）关于y轴对称的点的坐标是.

查看试题解析
13. 在 $△ A B C$ 中， $A B = A C$ ，周长为12.设 $B C = y$ ， $A B = x$ ，则y关于x的函数表达式为.

查看试题解析
14. 如图，等边三角形ABC的角平分线AD，BE交于点O，则 $∠ B O D =$ 度.

查看试题解析
15. 如图，一次函数的图象与y轴交于点 $(0 ， 2)$ .当 $y < 2$ 时，自变量x的取值范围是.

查看试题解析
16. 如图，已知 $A (1 ， 6)$ 为直线 $l ： y = - 2 x + b$ 上一点，先将点A向下平移a个单位长度，再向右平移4个单位长度至点B，再将点B向下平移a个单位长度至点C.若点C恰好落在直线l上，则a的值为.

查看试题解析
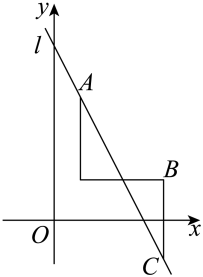17. 如图，在 $△ A B C$ 中，AE是BC边上的中线，过点C作 $C D ⊥ A E$ ，交AE的延长线于点D，连结BD.若 $A B = B D$ ， $△ B C D$ 的面积为10，则 $△ A B C$ 的面积为.

查看试题解析
18. 如图，在长方形球桌ABCD上，母球P在边AB处被击中后依次在边BC，CD，DA上的E，F，G三点反弹，最终停在边AB上的点Q处.若 $B P = 100 c m$ ， $A Q = 60 c m$ ， $C E = B E$ ，则PQ的长cm.

查看试题解析

三、解答题

19. 解不等式组 ${\begin{array}{l} 5 x + 12 \geq 2 ， \\ \frac{2 x - 1}{3} < 1 ， \end{array}$ 并把解表示在数轴上．

查看试题解析
20. 如图，在 $△ A B C$ 中， $A B = A C$ ， D是BC的中点， $D E ⊥ A B$ ， $D F ⊥ A C$ ，点E，F分别为垂足.求证： $D E = D F$ .
针对这道题，三位同学进行了如下讨论
小温：“需要利用全等证明.”
小州：“要证线线段相等，我想到了角平分线.”
小市：“我觉得你们都对，但还有别的方法.”
请你结合上述讨论，选择恰当的方法完成证明.

查看试题解析
21. 在平面直角坐标系中，我们把横、纵坐标都为整数的点称为整点，记顶点都是整点的三角形为整点三角形.如图，已知整点 $A (2 ， 2)$ ， $B (3 ， 5)$ ，请在所给的网格区域（含边界）按要求画整点三角形.

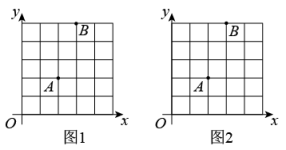(1)、在图1中画一个 $△ A B C$ 使点C的横、纵坐标的平方和等于25.

(2)、在图2中画一个 $△ O B D$ 使点D的横、纵坐标之和等于4，且点A在 $△ O B D$ 的内部.

查看试题解析
22. 如图，直线 $y = x + 3$ 分别交x轴、y轴于点A，B，直线 $y = - 3 x + b$ 经过点B，交x轴于点C，以BC为斜边向左侧作等腰 $R t △ B C D$ .

(1)、求b的值和OC的长.

(2)、连结OD，求 $∠ A O D$ 的度数.

(3)、设点D到AB，AC，BC的距离分别为 $d_{1}$ ， $d_{2}$ ， $d_{3}$ ，求 $d_{1}$ ， $d_{2}$ ， $d_{3}$ 之比.

查看试题解析

23. 项目化成果展示了一款简易电子秤：可变电阻上装有托盘（质量忽略不计），测得物品质量x（kg）与可变电阻y（Ω）的多组对应值，画出函数图象（如图1）.图2是三种测量方案，电源电压恒为8V，定值电阻为30Ω，与可变电阻串联.

【链接】串联电路中，通过两个电阻的电流I相等， $I = \frac{U}{R}$ .可变电阻、定值电阻两端的电压之和为8V，则有 $I (y + 30) = 8$ .

(1)、求y关于x的函数表达式，并写出自变量x的取值范围.

(2)、三个托盘放置不同物品后，电表A，

V_{0}

，

V_{1}

的读数分别为0.1A，6V，4V.请从以下方案中选择一个，求出对应物品的质量是多少kg？

(3)、小明家买了某散装大米65kg，为了检验商家是否存在缺斤少两的情况，请你将大米分批称重，用方案一、二、三来进行检验，设大米为

a (60 < a \leq 65) k g

，前两次称合适的千克数，第3次用含a的代数式表示，请填写下表.

	第1次（方案一）	第2次（方案二）	第3次（方案三）
大米（kg）
读数	I＝ A	$V_{0}$ ＝ V	$V_{1} \geq$ V

查看试题解析