浙江省台州市温岭市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列四个图标中，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列长度的三条线段能组成三角形的是（）

A、3cm、 3cm、6cm B、3cm、5cm、7cm C、2cm、4cm、6cm D、2cm、9cm、6cm

查看试题解析
3. 要使分式 $\frac{x + 1}{x - 1}$ 有意义，则x的取值应满足（）

A、x≠±1 B、x＞1 C、x≠－1 D、x≠1

查看试题解析
4. 下列各式从左到右的变形中，属于因式分解的是（）

A、（x＋3）（x-3）＝x²-9 B、2ab-2ac ＝2a（b-c） C、（m＋1）²＝m²＋2m＋1 D、n²＋2n＋1＝n（n＋2）＋1

查看试题解析
5. 下列运算正确的是（）

A、（-a）² ＝-a² B、2a² -a² ＝ -a² C、a^-1·a³＝a² D、（a-1）² ＝a²

查看试题解析
6. 一个多边形的每一个外角都为72°，这个多边形是（）

A、五边形 B、六边形 C、八边形 D、十边形

查看试题解析
7. 如图，OP平分∠AOB，E为OA上一点，OE＝4，P到OB的距离是2，则△OPE的面积为（）

A、2 B、3 C、4 D、8

查看试题解析
8. 如图，点C在线段BG上的一点，以BC，CG为边向两边作正方形，面积分别是S₁和S₂ ，两正方形的面积和S₁+S₂=40，已知BG=8，则图中阴影部分面积为（）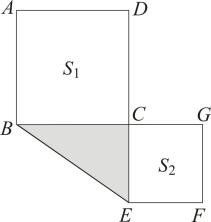

A、6 B、8 C、10 D、12

查看试题解析
9. 如图，玩具车从A点出发，向西走了a米，到达B点，然后顺时针旋转120°，前进b米，到达C点，再顺时针旋转120°，前进c米，到达D点，D点刚好在A点的正北方向，则a、b、c之间的关系为（）

A、a＋c＝b B、2a＝b＋c C、4c＝a＋b D、 $\frac{1}{2}$ a＝b－c

查看试题解析
10. 如图，直角三角形ABC中，AC＝BC，AD是△ABC的角平分线，动点M、N同时从A点出发，以相同的速度分别沿A→C→B和A一B→C方向运动，并在边BC上的点E相遇，连接AE，①AE平分△ABC的周长，②AE是△ABD的角平分线，③AE是△ABD的中线.以上结论正确的有（）

A、①② B、①③ C、②③ D、①②③

查看试题解析

二、填空题

11. 计算：（a+2b）（a﹣2b）=

查看试题解析
12. 若把分式 $\frac{x + 3 y}{2 x}$ 的x、y同时扩大10倍，则分式的值（填变大，变小，不变）

查看试题解析
13. 如图所示的五边形花环是用五个全等的等腰三角形拼成的，则∠BAC的度数为.

查看试题解析
14. 如果等腰三角形的一个角比另一个角大30° ，那么它的顶角是度

查看试题解析
15. 已知 $\frac{a ＋ b}{a - b}$ ＝3²⁰ ， a²－b²＝3²² ，则a－b＝.

查看试题解析
16. 如图，△ABC中，AB＝AC，BC＝ $\sqrt{3}$ ， AB的垂直平分线交BC于点D.且BD＜CD，过点B作射线AD的垂线，垂足为E，则CD $-$ DE＝.

查看试题解析

三、解答题

17. 计算：

(1)、用简便方法计算：101²－99²

(2)、因式分解：2a²＋12ab＋18b²

查看试题解析
18. 先化简，后求值： $\frac{x^{2} - 4 y^{2}}{4 x^{2} - 8 x y}$ ，其中x＝ $- \frac{1}{2}$ ， y＝ $\frac{1}{4}$

查看试题解析
19. 已知：如图，点B、E、C、F在一条直线上，AB∥DE，AB＝DE.BC＝EF；

(1)、求证：△ABC≌△DEF；

(2)、若点E为BC中点，EC＝6，求线段BF的长度.

查看试题解析
20. 如图，D是Rt△ABC斜边BC上的一点，连接AD，将△ACD沿AD翻折得△AFD，恰有AF⊥BC，

(1)、若∠C＝35°，∠BAF＝；

(2)、试判断△ABD的形状，并说明理由.

查看试题解析
21. 如图，图中的小方格都是边长为1的正方形，

(1)、画出△ABC关于y轴的对称图形△A₁B₁C₁ ，并直接写出△A₁B₁C₁的各顶点坐标：

(2)、P为x轴上一动点，连接PB，PC，当PB＋PC的值最小时，请在图中作出点P，（保留作图痕迹）并直接写出点P的坐标为（）.

查看试题解析
22. 杭绍台高铁开通后，相比原有的“杭甬一甬台”铁路，全程平均速度提高了50%，温岭站到杭州东站的里程缩短了50km.行车时间减少了50分钟.测得杭绍台高铁从温岭站到杭州东站全程共s km.

(1)、求杭绍台铁路的平均速度（用含s的式子表示）：

(2)、因设计原因，列车在杭甬线的平均速度与在杭绍台的平均速度相同，杭甬线与甬台线的线路里程之比为4：5，求列车在甬台线的平均速度.

查看试题解析
23. 学习了平方差、完全平方公式后，小聪同学对学习和运用数学公式非常感兴趣，他通过上网查阅，发现还有很多数学公式，如立方和公式：（a＋b）（a²－ab＋b²）＝a³＋b³ ，他发现，运用立方和公式可以解决很多数学问题，请你也来试试利用立方和公式解决以下问题：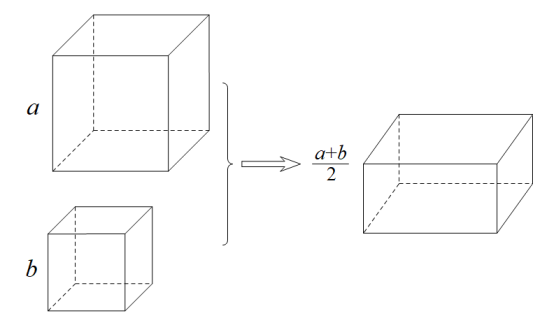

(1)、【公式理解】公式中的字母可以代表任何数、字母或式子
①化简：（a－b）（a²＋ab＋b²）＝；
②计算：（99³＋1）÷（99²－99＋1）＝；

(2)、【公式运用】已知： $\frac{1}{x}$ ＋x＝5，求 $[(\frac{1}{x})^{2} + x] \div (\frac{1}{x} + 1)$ 的值：

(3)、【公式应用】如图，将两块棱长分别为a、b的实心正方体橡皮泥揉合在一起，重新捏成一个高为 $\frac{a + b}{2}$ 的实心长方体，问这个长方体有无可能是正方体，若可能，a与b应满足什么关系？若不可能，说明理由.

查看试题解析
24. 如图1，已知AB＝AC，D是AC上一个动点，E、C位于BD两侧，BD＝BE，∠BAC＝∠DBE；

(1)、当∠BAC＝60°时，如图2，连接AE，求证：AE＝CD；

(2)、当∠BAC＝45°时，
①若DE⊥AB，则∠CDB＝度；
②如图4，连接AE.当∠CDB＝度时，AE最小；

(3)、当∠BAC＝90°时，如图5，连接CE交AB于点M，求 $\frac{C D}{А М}$ 的值.

查看试题解析