浙江省台州市临海市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 某班开展了以迎2022年北京冬奥为主题的海报评比活动.下列海报设计中，属于轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 中科院发现“绿色”光刻胶，精度可达0.00000000014米，数字0.00000000014用科学记数法可表示为（）

A、 $14 \times 1 0^{- 7}$ B、 $1.4 \times 1 0^{- 8}$ C、 $1.4 \times 1 0^{- 9}$ D、 $1.4 \times 1 0^{- 10}$

查看试题解析
3. 若三角形的两边长为2和3，则第三边长可以是（）

A、1 B、3 C、5 D、7

查看试题解析
4. 一个正多边形的每个外角都等于60°，那么它的边数是（）

A、6 B、8 C、10 D、12

查看试题解析
5. 如图，有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度 $A C$ 与右边滑梯的水平长度 $D F$ 相等，那么判定 $△ A B C$ 与 $△ D E F$ 全等的依据是（）

A、 $H L$ B、 $A S A$ C、 $A A S$ D、 $S S S$

查看试题解析
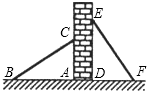6. 下列运算中，计算结果正确的是（）

A、 $m^{10} ÷ m^{2} = m^{5}$ B、 ${(2 m)}^{2} = 2 m^{2}$ C、 $m^{3} \cdot m^{2} = m^{5}$ D、 $m^{3} + m^{2} = m^{5}$

查看试题解析
7. 如图，△ABC中，AB=AC，D是BC中点，下列结论中不正确的是（）

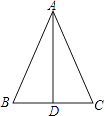A、∠B=∠C B、AD⊥BC C、AD平分∠BAC D、AB=2BD

查看试题解析
8. 如果把分式 $\frac{x}{x - y}$ 中的x，y都扩大为原来的3倍，那么分式的值（）

A、缩小为原来的3倍 B、不变 C、扩大为原来的3倍 D、扩大为原来的9倍

查看试题解析
9. 如图，点E在正方形 $A B C D$ 的边 $A B$ 上的一个动点（不与点A，B重合），以 $A E$ 为边在正方形 $A B C D$ 内部作正方形 $A E F G$ ，延长 $G F$ 交边 $B C$ 于点M，延长 $E F$ 交 $D C$ 于点N，则四边形 $F M C N$ 也是正方形.若 $A B = a$ ， $A E = b$ ，则由这个图形可以说明下列不等式关系一定成立的是（）

A、 $a^{2} - 2 a b + b^{2} < a b$ B、 $a^{2} - 2 a b + b^{2} < 2 a b - b^{2}$ C、 ${(a - b)}^{2} < a^{2} - b^{2}$ D、 $(a + b) (a - b) < b^{2}$

查看试题解析
10. 如图，在 $R t △ A B C$ 中， $∠ A = 90 °$ ， $∠ C = 30 °$ ， $A B = 1$ ， $A C = \sqrt{3}$ ，动点P在边 $A B$ 上，点P关于 $B C$ ， $A C$ 的对称点分别为点E，F，连接 $E F$ ，交 $A C$ ， $B C$ 分别为点M，N.
甲：我发现线段 $E F$ 的最大值为2，最小值为 $\sqrt{3}$ ；
乙：我连接 $P M$ ， $P N$ ，发现 $△ P M N$ 一定为钝角三角形.
则下列判断正确的是（）

A、甲对乙对 B、甲对乙错 C、甲错乙对 D、甲错乙错

查看试题解析

二、填空题

11. 如图所示的自行车架设计成三角形，这样做的依据是三角形具有.

查看试题解析
12. 因式分解： $x^{2} - 4 =$ .

查看试题解析
13. 点P（1，2）关于y轴对称的点的坐标是.

查看试题解析
14. 分式 $\frac{2}{a - 1}$ 有意义的条件是.

查看试题解析
15. 如图，在 $△ A B C$ 中， $C D$ 是 $∠ A C B$ 的平分线，延长 $C D$ 至点E，使 $D E = \frac{1}{2} C D$ ，连接 $B E$ ，若 $A C = 2 B C$ ， $△ B D E$ 的面积为1，则 $△ A B C$ 的面积是.

查看试题解析
16. 如图，在 $△ A B C$ 中，点P为 $A B$ 和 $B C$ 垂直平分线的交点，点Q与点P关于 $A C$ 对称，连接 $P C$ ， $P Q$ ， $C Q$ .若 $△ P C Q$ 中有一个角是50°，则 $∠ B =$ 度.

查看试题解析

三、解答题

17. 计算

(1)、 $202 2^{0} - 2^{- 1}$ ；

(2)、 $x (x - 2) + {(x + 1)}^{2}$ .

查看试题解析
18. 先化简 $\frac{2 x}{{(x - 1)}^{2}} - \frac{2}{{(x - 1)}^{2}}$ ，再从0，1两个数字中选取一个合适的数作为 $x$ 代入求值.

查看试题解析
19. 如图，点B，E，C，F在同一条直线上， $A B = D E$ ， $B E = C F$ ， $∠ B = ∠ D E F$ .求证： $△ A B C ≌ △ D E F$ .

查看试题解析
20. 如图，在 $5 \times 5$ 的网格纸中， $△ A B C$ 的三个顶点都在格点上，请仅用直尺，按要求画图.

(1)、在图1中画出过点B的直线l，使其平分 $△ A B C$ 的面积；

(2)、在图2中画出线段 $B D$ ，使其平分 $∠ A B C$ ，且点D在格点上.

查看试题解析
21. 如图，已知 $△ A B C$ ，点D在边 $A B$ 上.

(1)、求作点D，使点D到点B，C的距离相等；（尺规作图，保留作图痕迹，不写作法）

(2)、连接 $D C$ ，已知 $∠ B = 32 °$ ，求 $∠ A D C$ 的度数.

查看试题解析
22. 把1，3，5，7，9…这一组数按如下规律排放在表格1中，任意选定如图所示方框中4个数，进行交叉相乘再相减的运算，即 $b c - a d$ ，例如： $9 \times 17 - 7 \times 19 = 20$ .完成下列各题：

(1)、计算： $3 \times 11 - 1 \times 13 =$ ；

(2)、猜想： $b c - a d =$ ；

(3)、验证：请你利用整式的运算对以上的规律加以证明；

(4)、拓展，如表2，把1，3，5，7，9…这一组数重新排放在有n列的表格中，则 $b c - a d =$ .（用含n的式子表示）

查看试题解析
23. 某水果商两次去批发市场采购同一种水果，第一次用2000元购进了若干千克，很快卖完，第二次用3000元所购数量比第一次多100千克，且每千克的进价比第一次提高了20%.

(1)、求第一次购买水果的进价；

(2)、求第二次购买水果的数量：

(3)、该水果商按以下方案卖出第二批的水果：先以a元/千克的价格售出m千克，再以8元/千克的价格售出剩余的全部水果，共获利1600元.若a，m均为整数，且a不超过第二次进价的2倍，求a和m的值.

查看试题解析
24. 如图1，已知 $∠ E A F = 30 °$ ，定点P在射线 $A E$ 上，动点B在射线 $A F$ 上，作凸四边形 $A B P C$ ，使 $P C = P B$ ，且 $∠ C P B = 150 °$ .

(1)、如图1，当 $∠ P B A$ 为锐角时.
①若 $∠ P B A = α$ ，试用含 $α$ 的式子表示 $∠ C P A$ ；
②过点C作 $C H ⊥ A P$ 于点H，求证： $C H = \frac{1}{2} A P$ .

(2)、如图2，当点B运动到 $P C ∥ A B$ 时，连接 $B C$ 交 $A P$ 于点K，试用等式表示线段 $P C$ ， $P K$ ， $A B$ 之间的数量关系，并说明理由；

(3)、若点B关于直线 $A P$ 的对称点为点D，连接 $D P$ ， $D C$ ，当 $△ D P C$ 为等腰直角三角形时，请直接写出 $\frac{S_{△ P A C}}{S_{△ P C D}}$ 的值.

查看试题解析