浙江省台州市椒江区2021-2022年八年级上学期期末数学试题
试卷更新日期:2022-11-16 类型:期末考试
一、单选题
-
1. 下面4个手机软件图标为轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 要使分式有意义,则x应满足的条件是( )A、x>1 B、x>-1 C、x≠1 D、x≠-13. 下列计算正确的是( )A、 B、 C、 D、4. 如图,在中, , , 是的平分线,于点H,则的度数是( )
2. 要使分式有意义,则x应满足的条件是( )A、x>1 B、x>-1 C、x≠1 D、x≠-13. 下列计算正确的是( )A、 B、 C、 D、4. 如图,在中, , , 是的平分线,于点H,则的度数是( )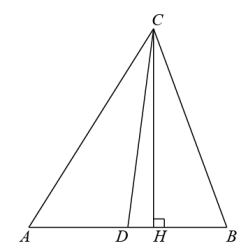 A、 B、 C、 D、5. 小明在学习了全等三角形的相关知识后,发现了一种测量距离的方法.如图,小明直立在河岸边的O处,他压低帽子帽沿,使视线通过帽沿,恰好落在河对岸的A处,然后转过身,保持和刚才完全一样的姿势,这时视线落在水平地面的B处(A,O,B三点在同一水平直线上),小明通过测量O,B之间的距离,即得到O,A之间的距离.小明这种方法的原理是( )
A、 B、 C、 D、5. 小明在学习了全等三角形的相关知识后,发现了一种测量距离的方法.如图,小明直立在河岸边的O处,他压低帽子帽沿,使视线通过帽沿,恰好落在河对岸的A处,然后转过身,保持和刚才完全一样的姿势,这时视线落在水平地面的B处(A,O,B三点在同一水平直线上),小明通过测量O,B之间的距离,即得到O,A之间的距离.小明这种方法的原理是( ) A、 B、 C、 D、6. 如图,在中, , , 平分 , 若 , 则点D到的距离是( )
A、 B、 C、 D、6. 如图,在中, , , 平分 , 若 , 则点D到的距离是( ) A、2 B、3 C、4.5 D、67. 若 , , 则的值是( )A、7 B、18 C、24 D、638. 将一个正三角形、一个正方形、一个正五边形以为公共边如图摆放,则的度数是( )
A、2 B、3 C、4.5 D、67. 若 , , 则的值是( )A、7 B、18 C、24 D、638. 将一个正三角形、一个正方形、一个正五边形以为公共边如图摆放,则的度数是( )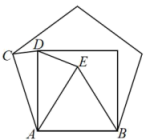 A、 B、 C、 D、9. 设a,b都是不为0的实数,且 , , 定义一种新运算: , 则下面四个结论正确的是( )A、 B、 C、 D、10. 如图,在中, , 过点C作于点D,点E是上一点,将沿着翻折得到 , 连接 , 若E,F,B三点恰好在同一条直线上,则的度数是( )
A、 B、 C、 D、9. 设a,b都是不为0的实数,且 , , 定义一种新运算: , 则下面四个结论正确的是( )A、 B、 C、 D、10. 如图,在中, , 过点C作于点D,点E是上一点,将沿着翻折得到 , 连接 , 若E,F,B三点恰好在同一条直线上,则的度数是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 新冠疫情期间,佩戴口罩是目前核心预防方法之一,口罩能够过滤掉的最小的颗粒直径是0.0000003米,其中0.0000003米用科学记数法表示是米.12. 因式分解:x-xy2=.13. 一个等腰三角形的两边长分别为4cm和9cm,则它的周长为cm.14. 如图,在中, , , 点A的坐标 , 点B的坐标 , 则点C的坐标是.
 15. 如图,在等边中,是的平分线,点E是的中点,点P是上的一个动点,连接 , , 当的值最小时,的度数为.
15. 如图,在等边中,是的平分线,点E是的中点,点P是上的一个动点,连接 , , 当的值最小时,的度数为.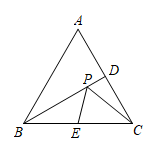 16. 如图,两个正方形的边长分别为a,b,如果 , , 则图中阴影部分的面积是.
16. 如图,两个正方形的边长分别为a,b,如果 , , 则图中阴影部分的面积是.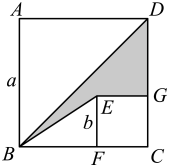
三、解答题
-
17. 计算:(1)、(2)、.18. 先化简,再求值: ,其中 .19. 如图,两条公路 , 相交于点O,在内部有两个村庄C,D.为方便群众接种新冠疫苗,该地决定在内部再启动一个方舱式接种点P,要求同时满足:

(1)到两条公路 , 的距离相等.
(2)到两村庄C,D的距离相等.请你用直尺和圆规作出接种点P的位置(保留作图痕迹).20. 如图,点F,C在线段上,.求证:.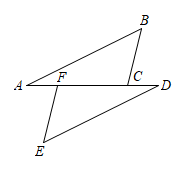 21. 先阅读材料,再解答问题.
21. 先阅读材料,再解答问题.我们已经知道,完全平方公式可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式来表示,例如,就可以用图1或图2等图形的面积表示.
 (1)、请写出图3中所表示得代数恒等式.(2)、试画出一个几何图形,使它的面积能表示代数恒等式:.22. 秋冬季新冠疫情形式严峻,台州某口罩厂接到540万只口罩的紧急生产任务,为了尽快完成任务,该口罩厂实际每天生产的口罩数量比原计划每天多 , 结果提前3天完成任务,那么实际每天生产口罩多少万只?23. 2021年世界机器人大会9月份在北京举行,我国机器人产业迎来升级换代、跨越发展的窗口期.某校机器人兴趣小组开发了一种水陆两栖探测型机器人,它可以准确勘测到目标物相对于自身的方位.某日在如图所示场地训练时,机器人从A地出发,全程沿着正北方向移动,以一定的陆行速度移动到河岸线b上的B地后切换到水栖模式下水,在正北方向的C地上岸后,移动速度比原来的陆行速度降低了 , 到D地后停下.下表是机器人训练过程中记录的部分信息(目标物P固定在河岸线a上,).
(1)、请写出图3中所表示得代数恒等式.(2)、试画出一个几何图形,使它的面积能表示代数恒等式:.22. 秋冬季新冠疫情形式严峻,台州某口罩厂接到540万只口罩的紧急生产任务,为了尽快完成任务,该口罩厂实际每天生产的口罩数量比原计划每天多 , 结果提前3天完成任务,那么实际每天生产口罩多少万只?23. 2021年世界机器人大会9月份在北京举行,我国机器人产业迎来升级换代、跨越发展的窗口期.某校机器人兴趣小组开发了一种水陆两栖探测型机器人,它可以准确勘测到目标物相对于自身的方位.某日在如图所示场地训练时,机器人从A地出发,全程沿着正北方向移动,以一定的陆行速度移动到河岸线b上的B地后切换到水栖模式下水,在正北方向的C地上岸后,移动速度比原来的陆行速度降低了 , 到D地后停下.下表是机器人训练过程中记录的部分信息(目标物P固定在河岸线a上,).
机器人所处位置
A
B
C
D
时间
13:00
13:40
数据丢失
14:40
目标物P相对于当前位置的方位角
北偏东15°
北偏东30°
正东
南偏东45°
(1)、探究线段与之间的数量关系,并证明你的结论.(2)、试求本次训练过程中机器人在水栖模式下过河(段)所用的时间.24. 如图1,在等边中,点D是边上的一点,连接 , 以为边作等边 , 连接. (1)、求证:.(2)、如图2,过A,D,E三点分别作于点F,于点M,于点N.求证:.(3)、如图3, , 垂足为点F,若将点D改为线段上的一个动点,连接 , 以为边作等边 , 连接.当时,直接写出的最小值.
(1)、求证:.(2)、如图2,过A,D,E三点分别作于点F,于点M,于点N.求证:.(3)、如图3, , 垂足为点F,若将点D改为线段上的一个动点,连接 , 以为边作等边 , 连接.当时,直接写出的最小值.