浙江省绍兴市嵊州市2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 下列长度的三条线段，首尾相接能构成三角形的是（　　）

A、1cm，2cm，3cm B、5cm，5cm，5cm C、2cm，5cm，8cm D、1.5cm，1.4cm，2.9cm

查看试题解析
2. 下列交通标志是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 如图所示，一扇窗户打开后，用窗钩AB即可固定，这里所用的几何原理是（）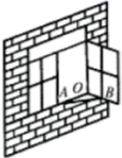

A、两点之间线段最短 B、垂线段最短． C、两定确定一条直线 D、三角形具有稳定性

查看试题解析
4. 如果m＞n，那么下列结论错误的是（）

A、m＋2＞n＋2 B、﹣2m＞﹣2n C、2m＞2n D、m﹣2＞n﹣2

查看试题解析
5. 如图，点B ， F ， C ， E共线，∠B=∠E ， BF=EC ，添加一个条件，不能判断△ABC≌△DEF的是（）

A、AB=DE B、∠A=∠D C、AC=DF D、AC∥FD

查看试题解析
6. 下列各数中，可以用来说明命题“任何偶数都是8的倍数”是假命题的反例是（　　）

A、9 B、16 C、8 D、4

查看试题解析
7. 如图，点 $A 、 B 、 C$ 都在方格纸的格点上，若点A的坐标为 $(0 ， 2)$ ，点B的坐标为 $(2 ， 0)$ ，则点C的坐标是（）

A、 $(2 ， 2)$ B、 $(1 ， 2)$ C、 $(1 ， 1)$ D、 $(2 ， 1)$

查看试题解析
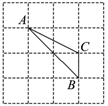8. 已知点A（2，y₁）和点B（a，y₂）在一次函数y＝﹣3x﹣b的图象上，且y₁＞y₂ ，则a的值可能是（）

A、3 B、0 C、﹣1 D、﹣2

查看试题解析
9. 如图，在△ABC中，CA=CB，∠ACB=110°，延长BC到D，在∠ACD内作射线CE，使得∠ECD=15°.过点A作AF⊥CE，垂足为F.若AF= $\sqrt{5}$ ，则AB的长为（　　）

A、 $\sqrt{10}$ B、2 $\sqrt{5}$ C、4 D、6

查看试题解析
10. 如图1，在平面直角坐标系中，长方形ABCD在第一象限，且BC $∥$ x轴，直线y＝ $\frac{1}{2}$ x-3沿x轴负方向平移，在平移过程中，直线被长方形ABCD截得的线段长为l，直线在x轴上平移的距离为m.图2是l与m之间的函数图象，则长方形ABCD的面积为（　　）

A、2 $\sqrt{5}$ B、6 C、8 D、12

查看试题解析

二、填空题

11. 平面直角坐标系中，点A(1，－2)在第象限.

查看试题解析
12. 命题“全等三角形的面积相等”的逆命题是命题．（填入“真”或“假”）

查看试题解析
13. 如图，两根竹竿AB和DB斜靠在墙CE上，量得∠CAB＝33°，∠CDB=21°，则∠ABD的度数为 .

查看试题解析
14. 等腰三角形的两边分别为4和6，则等腰三角形的周长为.

查看试题解析
15. 如图，由图象得方程组 ${\begin{array}{l} 3 x + y = 0 \\ y = x + 4 \end{array}$ 的解为 .

查看试题解析
16. 如图，在△ABC中，AD⊥BC于点D，AD与BE相交于点F，且AC=BF，DF=DC.若∠ABE=15°，则∠DBF的度数为.

查看试题解析
17. 如图，在平面直角坐标系中，已知点A（2，3），B（-2，1），在x轴上找一点P，使PA+PB的值最小，则点P的坐标为.

查看试题解析
18. 关于 $x$ 的不等式组 ${\begin{array}{l} 3 x - a \geq 0 \\ 2 x - b \leq 0 \end{array}$ 只有一个解，则 $a$ 与 $b$ 的关系是．

查看试题解析
19. 如图，在 $△ A B C$ 中， $∠ B A C > 90 °$ ，分别以点A ， B为圆心，以大于 $\frac{1}{2} A B$ 长为半径画弧，两弧交于点D ， E ．作直线DE ，交BC于点M ．分别以点A ， C为圆心，以大于 $\frac{1}{2} A C$ 长为半径画弧，两弧交于点F ， G ．作直线FG ，交BC于点N ．连接AM ， AN ．若 $∠ B A C = α$ ，则 $∠ M A N =$ ．

查看试题解析
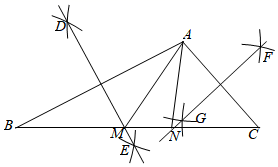20. 如图，在△ABC中，∠ACB=90°，AC=8，BC=6，D是线段AB的中点，P为直线BC上的一动点，连结DP.过点D作ED⊥DP，交直线AC于点E，连结EP.若CP=3，则AE的长为.

查看试题解析

三、解答题

21. 已知点A（2，3），点B与点A关于y轴对称，点C与点A关于x轴对称.

(1)、在所给的平面直角坐标系中作出△ABC.

(2)、求线段BC的长.

查看试题解析
22. 解不等式（组）：

(1)、5x-2＞3（x-2）

(2)、 ${\begin{array}{l} 3 x + 6 \geq 4 \\ \frac{x + 7}{3} > 2 x - 1 \end{array}$

查看试题解析
23. 为庆祝伟大的中国共产党成立100周年，发扬红色传统，传承红色精神，某学校举行了主题为“学史明理，学史增信，学史崇德，学史力行”的党史知识竞赛，一共有25道题，满分100分，每一题答对得4分，答错扣1分，不答得0分.

(1)、若某参赛同学只有一道题没有作答，最后他的总得分为86分，则该参赛同学一共答对了多少道题？

(2)、若规定参赛者每道题都必须作答且总得分大于或等于90分才可以被评为“学党史小达人”，则参赛者至少需答对多少道题才能被评为“学党史小达人”？

查看试题解析
24. 某销售公司推销一种产品，每月付给销售人员的工资有两种方案.
方案一：没有底薪，只付销售提成；

方案二：底薪加销售提成.

设x（件）是推销产品的数量，y（元）是销售人员的月工资.如图所示，y₁为方案一的函数图象，y₂为方案二的函数图象.

(1)、分别求y₁ ， y₂关于x 的函数表达式；

(2)、若该公司某销售人员1月份推销产品的数量没有超过70件，但其1月份的工资超过2000元.公司采用哪种方案给这名销售人员付1月份的工资?

查看试题解析
25.

(1)、【问题提出】已知：如图1，AD⊥DE于点D，BELDE于点E，点C在线段DE上，AC=BC且AC上BC，求证：△ADC≌△CEB.

(2)、【问题解决】
如图2，点D，C，E在直线1上.点A，B在l的同侧，AC⊥BC，若AD=AC=BC=BE=5cm，CD=6cm，求CE的长.

查看试题解析
26. 在平面直角坐标系xOy中，点B的坐标为（0，4 $\sqrt{3}$ ），以OB为边在y轴的右侧作正三角形OAB.AC⊥y轴，垂足为C.

(1)、如图1，求点A的坐标.

(2)、点D在线段AC上，点E是直线AB上一动点，连接DE、以DE为边作正三角形DEF（点D，E，F按逆时针排列）
①如图2，当点E与点A重合时，连接OD，BF.若BF=2 $\sqrt{7}$ ，求点D的坐标.
②若CD=2，点P是直线DF与直线OA的交点，当OP= $\sqrt{3}$ 时，直接写出点E的坐标.

查看试题解析