浙江省宁波市慈溪市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-11-16 类型:期末考试
一、单选题
-
1. 在下列交通标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知三角形的两边长为2,4,则第三边长应为( )A、6 B、5 C、2 D、13. 若 , 则下列式子中一定成立的是( )A、 B、 C、 D、4. 下列各点在一次函数的图象上的是( )A、 B、 C、 D、5. 如图,为测量桃李湖两端AB的距离,南开中学某地理课外实践小组在桃李湖旁的开阔地上选了一点C,测得∠ACB的度数,在AC的另一侧测得∠ACD=∠ACB,CD=CB,再测得AD的长,就是AB的长.那么判定△ABC≌△ADC的理由是( )
2. 已知三角形的两边长为2,4,则第三边长应为( )A、6 B、5 C、2 D、13. 若 , 则下列式子中一定成立的是( )A、 B、 C、 D、4. 下列各点在一次函数的图象上的是( )A、 B、 C、 D、5. 如图,为测量桃李湖两端AB的距离,南开中学某地理课外实践小组在桃李湖旁的开阔地上选了一点C,测得∠ACB的度数,在AC的另一侧测得∠ACD=∠ACB,CD=CB,再测得AD的长,就是AB的长.那么判定△ABC≌△ADC的理由是( ) A、SAS B、SSS C、ASA D、AAS6. 下列命题的逆命题是假命题的是( )A、两直线平行,同位角相等 B、线段垂直平分线上的点到线段两端距离相等 C、对顶角相等 D、等腰三角形两腰上的高线相等7. 如图,已知点A(2,3),B(5,1),若将线段AB平移至A1B1 , A1在y轴正半轴上,B1在x轴上,则A1的纵坐标、B1的横坐标分别为( )
A、SAS B、SSS C、ASA D、AAS6. 下列命题的逆命题是假命题的是( )A、两直线平行,同位角相等 B、线段垂直平分线上的点到线段两端距离相等 C、对顶角相等 D、等腰三角形两腰上的高线相等7. 如图,已知点A(2,3),B(5,1),若将线段AB平移至A1B1 , A1在y轴正半轴上,B1在x轴上,则A1的纵坐标、B1的横坐标分别为( ) A、2,3 B、1,4 C、2,2 D、1,38. 已知不等式的解是 , 下列有可能是函数的图像的是( )A、
A、2,3 B、1,4 C、2,2 D、1,38. 已知不等式的解是 , 下列有可能是函数的图像的是( )A、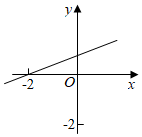 B、
B、 C、
C、 D、
D、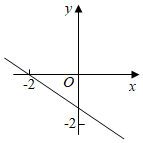 9. 某大型超市购进一批特种水果,运输过程中质量损失 , 假设不计超市其它费用,如果超市要想至少获得的利润,那么这种水果的售价在进价的基础上应至少提高( )A、 B、 C、 D、10. 如图,点A,B分别为x轴、y轴上的动点, , 点M是的中点,点 , , 过C作轴.点P为直线上一动点,则的最小值为( )
9. 某大型超市购进一批特种水果,运输过程中质量损失 , 假设不计超市其它费用,如果超市要想至少获得的利润,那么这种水果的售价在进价的基础上应至少提高( )A、 B、 C、 D、10. 如图,点A,B分别为x轴、y轴上的动点, , 点M是的中点,点 , , 过C作轴.点P为直线上一动点,则的最小值为( ) A、 B、9 C、 D、
A、 B、9 C、 D、二、填空题
-
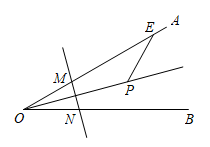
11. 能说明命题:“ , 则”是假命题的反例是.12. 已知y与x成正比例,当时, , 则当时,.13. 等腰三角形的一个内角是 ,则它的顶角度数是 .14. 关于x的一元一次不等式组恰有一个整数解,则m的取值范围是 .15. 如图, , 点P为的角平分线上一点,的垂直平分线交 , 分别于点M,N,点E为上异于点M的一点,且 , 则的面积为.
 16. 如图,在平面直角坐标系中,已知点A在直线:上,点B在直线:上,若是以点B为直角顶点的等腰直角三角形,则点A的坐标为.
16. 如图,在平面直角坐标系中,已知点A在直线:上,点B在直线:上,若是以点B为直角顶点的等腰直角三角形,则点A的坐标为.
三、解答题
-
17. 解一元一次不等式组: .18. 在平面直角坐标系中,已知的位置如图所示.
 (1)、请画出关于y轴对称的(其中点 , , 分别是点A,B,C的对应点,不写画法);(2)、写出点 , , 的坐标.19. 如图,在和中,B,E,C,F在同一直线上,下面给出四个论断:(1)、; (2); (3); (4).
(1)、请画出关于y轴对称的(其中点 , , 分别是点A,B,C的对应点,不写画法);(2)、写出点 , , 的坐标.19. 如图,在和中,B,E,C,F在同一直线上,下面给出四个论断:(1)、; (2); (3); (4).请把上述论断中的三个作为条件,余下的一个作为结论,写出一个真命题,并给出证明.
 20. 已知一次函数的图象过 , 两点.(1)、求该一次函数的表达式;(2)、当时,写出y的取值范围,请说明理由.21. 如图,在中,于点E.
20. 已知一次函数的图象过 , 两点.(1)、求该一次函数的表达式;(2)、当时,写出y的取值范围,请说明理由.21. 如图,在中,于点E. (1)、用直尺和圆规作于点D.(不写作法,保留作图痕迹)(2)、在(1)所画的图中,若.求证:.22. 如图,在等边中, , 点E,F分别为AB,BC的中点,点P从点C出发沿CA的方向运动,到点A停止运动,作线PF,记 , 点E到直线PF的距离.
(1)、用直尺和圆规作于点D.(不写作法,保留作图痕迹)(2)、在(1)所画的图中,若.求证:.22. 如图,在等边中, , 点E,F分别为AB,BC的中点,点P从点C出发沿CA的方向运动,到点A停止运动,作线PF,记 , 点E到直线PF的距离.
 (1)、按照下表中x的值补填完整表格(填准确值):
(1)、按照下表中x的值补填完整表格(填准确值):x
0
0.5
0.75
1
1.5
2
2.5
3
4
y
1.92
1.98
1.92
1.73
1.51
1.31
(2)、在坐标系中描出补全后的表中各组数值所对应的点 , 用光滑曲线连接;并回答变量y是x的函数吗?为什么?(3)、根据上述信息回答:当x在什么范围内时,y随x的增大而减小?当x取何值时,y的值最大,最大值是多少?23. 甲,乙两同学住在同一小区,是某学校的同班同学,小区和学校在一笔直的大街上,距离为2560米,在该大街上,小区和学校附近各有一个公共自行车取(还)车点,甲从小区步行去学校,乙比甲迟出发,步行到取车点后骑公共自行车去学校,到学校旁还车点后立即步行到学校(步行速度不变,不计取还车的时间).设甲步行的时间为x(分),图1中的线段OM和折线分别表示甲、乙同学离小区的距离y(米)与x(分)的函数关系的图象;图2表示甲、乙两人的距离s(米)与x(分)的函数关系的图象(一部分).根据图1、图2的信息,解答下列问题: (1)、分别求甲、乙两同学的步行速度与乙骑自行车的速度;(2)、求乙同学骑自行车时,y与x的函数关系式和a的值;(3)、补画完整图2,并用字母标注所画折线的终点及转折点,写出它们的坐标.24. 如图,M,N分别为锐角边 , 上的点,把沿折叠,点O落在所在平面内的点C处.
(1)、分别求甲、乙两同学的步行速度与乙骑自行车的速度;(2)、求乙同学骑自行车时,y与x的函数关系式和a的值;(3)、补画完整图2,并用字母标注所画折线的终点及转折点,写出它们的坐标.24. 如图,M,N分别为锐角边 , 上的点,把沿折叠,点O落在所在平面内的点C处. (1)、如图1,点C在的内部,若 , , 求的度数.(2)、如图2,若 , , 折叠后点C在直线上方,与交于点E,且 , 求折痕的长.(3)、如图3,若折叠后,直线 , 垂足为点E,且 , , 求此时的长.
(1)、如图1,点C在的内部,若 , , 求的度数.(2)、如图2,若 , , 折叠后点C在直线上方,与交于点E,且 , 求折痕的长.(3)、如图3,若折叠后,直线 , 垂足为点E,且 , , 求此时的长.