浙江省丽水市青田县2021-2022学年八年级上学期期末数学试题

试卷更新日期：2022-11-16 类型：期末考试

进入 出卷网 下载

一、单选题

  • 1. 下列表情中属于轴对称图形的是（    ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 若−2x<5 ， 两边都除以-2，得（  ）
    A、x<−52 B、x>−52 C、x<−25 D、x>−25

    查看试题解析

  • 3. 下列命题中，是假命题的是（    ）
    A、两点之间线段最短 B、对于任意实数x，x2＜0 C、对顶角相等 D、2是无理数

    查看试题解析

  • 4. 等腰三角形的一个外角是80°，则它的底角的度数为（    ）
    A、100° B、100°或40° C、50° D、40°

    查看试题解析

  • 5. 如图，把两根木条AB和AC的一端A用螺栓固定在一起，木条AB自由转动至AB′位置．在转动过程中，下面的量是常量的为（  ）

    A、∠BAC的度数 B、AB的长度 C、BC的长度 D、△ABC的面积

    查看试题解析

  • 6. 如图，已知△ABC≌△DEF，B，E，C，F在同一条直线上.若BF＝8cm，BE＝2cm，则CE的长度（    ）cm.

    A、5 B、4 C、3 D、2

    查看试题解析

  • 7. 如图Rt△ABC中，∠BAC＝90°，分别以边AB，CA，BC向外作正方形，正方形ABIH的面积为25，正方形BDEC的面积为169，则正方形ACFG的面积是（ ）

    A、194 B、144 C、122 D、110

    查看试题解析

  • 8. 把线段“（x，－1）（1≤x≤5）”向左平移2个单位，所得的线段是（    ）
    A、（x，－1）（－1≤x≤3） B、（x＋2，－1）（1≤x≤5） C、（x，－3）（1≤x≤5） D、（x－2，－1）（－1≤x≤3）

    查看试题解析

  • 9. 如图，一直线与两坐标轴的正半轴分别交于A，B两点，P是线段AB上任意一点（不包括端点），过点P分别作两坐标轴的垂线与两坐标轴围成的长方形的周长为6，则该直线的函数表达式是（    ）

    A、y＝x＋3 B、y＝x＋6 C、y＝－x＋3 D、y＝－x＋6

    查看试题解析

  • 10. 在如图所示的方格纸中有四条线段a，b，c，d，通过平移其中两条线段，使得和第三条线段首尾相接组成一个三角形，则能组成三角形的不同平移方法有（    ）

    A、10种 B、11种 C、12种 D、13种

    查看试题解析

二、填空题

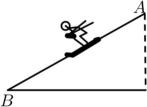
  • 11. 三角形的两边长分别为2cm和3cm，则此三角形第三边的长可以是cm（写出一个符合条件的即可）.

    查看试题解析

  • 12. 一次函数y＝10－2x的比例系数是.

    查看试题解析

  • 13. 如图，一名滑雪运动员沿着倾斜角为30°的斜坡，从A滑行至B，已知AB=100m ， 则这名滑雪运动员的高度下降了米.

    查看试题解析

  • 14. 已知线段AB=3 ， AB∥y轴，若点A的坐标为(1 ， 2) ， 则点B的坐标为.

    查看试题解析

  • 15. 关于x的不等式2x+a⩽1只有3个正整数解，则a的取值范围为。

    查看试题解析

  • 16. 如图，在平面直角坐标系中，边长为2的等边三角形ABC的顶点A，B分别在x轴正半轴和y轴正半轴上运动.

    (1)、当OB＝1时，点C的坐标为；
    (2)、连接OC，则OC的最大值为.

    查看试题解析

三、解答题

  • 17. 解不等式组{x+8>4x−13−5x<x−2(2x−1)

    查看试题解析

  • 18. 如图，四个三角形纸片Rt△ABC，Rt△AB1C1 ， Rt△AB2C2 ， Rt△AB3C3完全重合，并按图示位置摆放.已知BC＝10 ， AB＝1，求四边形CC1C2C3的面积.

    查看试题解析

  • 19. 一个四边形零件ABCD如图所示，通过实际测算得到AE＝170mm，EG＝150mm，GH＝110mm，DF＝150mm，CG＝110mm，BH＝150mm.
     

    (1)、选取适当的比例为 ， 建立适当的直角坐标系；
    (2)、在坐标系中作出这个四边形，并标出各顶点的坐标.

    查看试题解析

  • 20. 如图，已知AD是△ABC的角平分线，DE⊥AB于点E，DF⊥AC于点F，BE＝CF.

    (1)、求证：△ABC是等腰三角形；
    (2)、若AB＝5，BC＝6，求DE的长.

    查看试题解析

  • 21. 已知y是x的一次函数，当x＝－3时，y＝1；当x＝2时，y＝－14.
    (1)、求这个一次函数的表达式；
    (2)、当x＞－2时，求函数y的取值范围.

    查看试题解析

  • 22. 有一家庭工厂投资2万元购进一台机器，生产某种商品.这种商品每个的成本是3元，出售价是5元，应付的税款和其他费用是销售收入的10%.求：
    (1)、生产、销售一个这种商品的利润.
    (2)、至少需要生产、销售多少个这种商品，才能使所获利润（毛利润减去税款和其他费用）超过投资购买机器的费用？

    查看试题解析

  • 23. 如图，直线l∥线段BC，点A是直线l上一动点.在△ABC中，AD是△ABC的高线，AE是∠BAC的角平分线.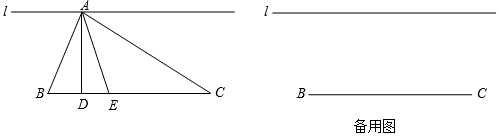

    (1)、如图，若∠ABC＝65°，∠BAC＝80°，求∠DAE的度数；
    (2)、当点A在直线l上运动时，探究∠BAD，∠DAE，∠BAE之间的数量关系，并画出对应图形进行说明.

    查看试题解析

  • 24. 小聪和小慧去某风景区游览，约好在飞瀑见面.上午7：00，小聪乘电动车从古刹出发，沿景区公路（图1）去飞瀑，车速为30km/h.小慧也于上午7：00从塔林出发，骑电动自行车沿景区公路去飞瀑，车速为20km/h.小聪离古刹的路程s1（km）与时间t（h）的函数关系如图2所示.试结合图中信息回答：

    (1)、写出小慧离古刹的路程s2（km）与时间t（h）的函数关系并画出其函数图象.
    (2)、当小聪到达飞瀑时，小慧离飞瀑还有多少千米？
    (3)、出发多少时间时，两人相距5km？

    查看试题解析