浙江省金华市东阳市2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-11-16 类型:期末考试
一、单选题
-
1. 以下是几个银行的图标,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在数轴上表示不等式x-1<0的解集,正确的是()A、
2. 在数轴上表示不等式x-1<0的解集,正确的是()A、 B、
B、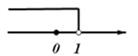 C、
C、 D、
D、 3. 如果 在y轴上,那么点P的坐标是( )A、 B、 C、 D、4. 能说明命题“对于任何实数a,都有 ”是假命题的反例是( )A、 B、 C、 D、5. 若等腰三角形中有两边长分别为4和5,则这个三角形的周长为( )A、13 B、12 C、12或13 D、13或146. 满足下列条件的△ABC中,不是直角三角形的是( )A、∠A:∠B:∠C=1:2:3 B、∠A+∠B=∠C C、∠A:∠B:∠C=3:4:5 D、一个外角等于和它相邻的内角7. 已知A(-3,4),B(2,-3),C(3,-4),D(-5,)与其它三个点不在同一正比例函数图象上的点是( )A、点A B、点B C、点C D、点D8. 如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=28°,则∠CDE=( )
3. 如果 在y轴上,那么点P的坐标是( )A、 B、 C、 D、4. 能说明命题“对于任何实数a,都有 ”是假命题的反例是( )A、 B、 C、 D、5. 若等腰三角形中有两边长分别为4和5,则这个三角形的周长为( )A、13 B、12 C、12或13 D、13或146. 满足下列条件的△ABC中,不是直角三角形的是( )A、∠A:∠B:∠C=1:2:3 B、∠A+∠B=∠C C、∠A:∠B:∠C=3:4:5 D、一个外角等于和它相邻的内角7. 已知A(-3,4),B(2,-3),C(3,-4),D(-5,)与其它三个点不在同一正比例函数图象上的点是( )A、点A B、点B C、点C D、点D8. 如图,在△ABC中,∠B=∠C,D为BC边上的一点,E点在AC边上,∠ADE=∠AED,若∠BAD=28°,则∠CDE=( ) A、 B、 C、 D、9. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于MN长为半径画弧,两弧交点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为( )
A、 B、 C、 D、9. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于MN长为半径画弧,两弧交点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为( )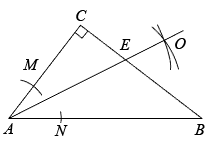 A、8 B、7 C、6 D、510. 如图①,在△ABC中,∠C=90°,∠A=30°,点D是AB边的中点,点P从点A出发,沿着AC-CB运动,到达点B停止.设点P的运动路径长为x,连DP,记△APD的面积为y,若表示y与x有函数关系的图象如图②所示,则△ABC的周长为( )
A、8 B、7 C、6 D、510. 如图①,在△ABC中,∠C=90°,∠A=30°,点D是AB边的中点,点P从点A出发,沿着AC-CB运动,到达点B停止.设点P的运动路径长为x,连DP,记△APD的面积为y,若表示y与x有函数关系的图象如图②所示,则△ABC的周长为( ) A、6+2 B、4+2 C、12+4 D、6+4
A、6+2 B、4+2 C、12+4 D、6+4二、填空题
-
11. 如图所示的两个三角形全等,则∠1的度数是 .
 12. 请你写出一个图像经过点(0,2),且y随x的增大而减小的一次函数解析式.13. 已知点A(m+1,1)与点B(2,n+1)关于x轴对称,则m+n的值为 .14. 函数y=kx+b图象如图所示,则关于x的不等式-kx-b>0的解集为 .
12. 请你写出一个图像经过点(0,2),且y随x的增大而减小的一次函数解析式.13. 已知点A(m+1,1)与点B(2,n+1)关于x轴对称,则m+n的值为 .14. 函数y=kx+b图象如图所示,则关于x的不等式-kx-b>0的解集为 . 15. 如图,在△ABC中,∠ACB=90°,AC=BC=4,动点D从点B出发,沿射线AB方向运动,以CD为边在右侧作等腰Rt△CDE,使∠DCE=90°,DC=EC,取BC中点F,连接EF,当EF的值最小时,AD=.
15. 如图,在△ABC中,∠ACB=90°,AC=BC=4,动点D从点B出发,沿射线AB方向运动,以CD为边在右侧作等腰Rt△CDE,使∠DCE=90°,DC=EC,取BC中点F,连接EF,当EF的值最小时,AD=. 16. 综合实践课上,小聪用一张长方形纸ABCD对不同折法下的折痕进行了探究,已知AB=12,∠CAB=30°,点E,F分别在AB,CD上,且AE=5,
16. 综合实践课上,小聪用一张长方形纸ABCD对不同折法下的折痕进行了探究,已知AB=12,∠CAB=30°,点E,F分别在AB,CD上,且AE=5, (1)、把长方形纸片沿着直线EF翻折,使点A的对应点A′恰好落在对角线AC上,点D的对应点为D′,如图①,则折痕EF长为 ;(2)、在EF,A′D′上取点G,H,沿着直线GH继续翻折,使点E与点F重合,如图②,则折痕GH长为 .
(1)、把长方形纸片沿着直线EF翻折,使点A的对应点A′恰好落在对角线AC上,点D的对应点为D′,如图①,则折痕EF长为 ;(2)、在EF,A′D′上取点G,H,沿着直线GH继续翻折,使点E与点F重合,如图②,则折痕GH长为 .三、解答题
-
17. 解不等式组 , 并将不等式组的解集表示在数轴上.
 18. 如图都是3×3的正方形网格,点A、B、C均在格点上.在给定的网格中,按下列要求画图:
18. 如图都是3×3的正方形网格,点A、B、C均在格点上.在给定的网格中,按下列要求画图: (1)、在图①中,画一条线段MN,使MN与AB关于某条直线对称,且M、N为格点.(2)、在图②中,画一个△DEF,使△DEF与△ABC关于某条直线对称,且D、E、F为格点,并写出符合条件的三角形共有 个.19. 如图,直线y=2x+4与x轴交于点A,与y轴交于点B.
(1)、在图①中,画一条线段MN,使MN与AB关于某条直线对称,且M、N为格点.(2)、在图②中,画一个△DEF,使△DEF与△ABC关于某条直线对称,且D、E、F为格点,并写出符合条件的三角形共有 个.19. 如图,直线y=2x+4与x轴交于点A,与y轴交于点B. (1)、求A,B两点的坐标.(2)、过B点作直线BP与x轴交于点P,且使OP=2OA,求直线BP的函数关系式.20. 如图,Rt△ACB中,∠ACB=90°,AC=BC,E点为线段CB一动点,连接AE,过点A作AF⊥AE且AF=AE,过点F作FD⊥AC于点D,如图①所示.
(1)、求A,B两点的坐标.(2)、过B点作直线BP与x轴交于点P,且使OP=2OA,求直线BP的函数关系式.20. 如图,Rt△ACB中,∠ACB=90°,AC=BC,E点为线段CB一动点,连接AE,过点A作AF⊥AE且AF=AE,过点F作FD⊥AC于点D,如图①所示. (1)、求证:FD=AC.(2)、若点E为BC中点,连BF交AC于点G,如图②,已知CG=1,求BC的长.21. 某校为“防疫知识小竞赛”准备奖品,购进A,B两种文具共40件作为奖品,设购进A种文具x件,总费用为y元.已知A、B文具的费用与x的部分对应数据如下表.
(1)、求证:FD=AC.(2)、若点E为BC中点,连BF交AC于点G,如图②,已知CG=1,求BC的长.21. 某校为“防疫知识小竞赛”准备奖品,购进A,B两种文具共40件作为奖品,设购进A种文具x件,总费用为y元.已知A、B文具的费用与x的部分对应数据如下表.x(件)
8
10
12
A种文具费用(元)
120
150
b
B种文具费用(元)
640
a
560
(1)、将表格补充完整:a=;b=;(2)、求y关于x的函数表达式;(3)、当A种文具的费用不大于B种文具的费用时,求总费用y的最小值.22. 小刚与小慧两人相约末登东舰峰,人距地面的高y(米)与登山时间x(分)之间函数图象如图所示,根据图象所提信息解答下列问题: (1)、小刚登山上升的速度是每分钟米,小慧在A地距地面的高度b为米;(2)、若小慧提速后,登山上升速度是小刚登山上升速度的3倍,请求出小慧登山全程中,距地面高度y(米)与登山时间x(分)之间的函数关系式;(3)、登山多长时间后,两人距地面的高度差为70米?23. 以△ABC的AB,AC为边作△ABD和△ACE,且AD=AB,AE=AC,∠DAB=∠CAE=α.CD与BE相交于O,连接AO,如图①所示.
(1)、小刚登山上升的速度是每分钟米,小慧在A地距地面的高度b为米;(2)、若小慧提速后,登山上升速度是小刚登山上升速度的3倍,请求出小慧登山全程中,距地面高度y(米)与登山时间x(分)之间的函数关系式;(3)、登山多长时间后,两人距地面的高度差为70米?23. 以△ABC的AB,AC为边作△ABD和△ACE,且AD=AB,AE=AC,∠DAB=∠CAE=α.CD与BE相交于O,连接AO,如图①所示. (1)、求证:BE=CD;(2)、判断∠AOD与∠AOE的大小,并说明理由.(3)、在EB上取使F,使EF=OC,如图②,请直接写出∠AFO与α的数量关系.24. 如图,直线y=-x+4交x轴,y轴分别为A、B,点P为x轴上的一个动点,过点P作PG⊥直线AB于点G.
(1)、求证:BE=CD;(2)、判断∠AOD与∠AOE的大小,并说明理由.(3)、在EB上取使F,使EF=OC,如图②,请直接写出∠AFO与α的数量关系.24. 如图,直线y=-x+4交x轴,y轴分别为A、B,点P为x轴上的一个动点,过点P作PG⊥直线AB于点G. (1)、求出点A、B的坐标,以及线段AB长.(2)、当点G与点B重合时,求△PAG的面积.(3)、连OG,当△POG为等腰三角形时,求点P的坐标.
(1)、求出点A、B的坐标,以及线段AB长.(2)、当点G与点B重合时,求△PAG的面积.(3)、连OG,当△POG为等腰三角形时,求点P的坐标.