浙江省湖州市长兴、安吉县2021-2022学年八年级上学期期末考试数学试题

试卷更新日期：2022-11-16 类型：期末考试

进入出卷网下载

一、单选题

1. 已知点 $A$ 的坐标为 $(- 1 ， 3)$ ，则点 $A$ 关于 $x$ 轴的对称点的坐标是（）

A、 $(1 ， - 3)$ B、 $(- 1 ， - 3)$ C、 $(- 1 ， 3)$ D、 $(1 ， 3)$

查看试题解析
2. 若一个三角形的两边长分别是2和4，则第三边的长可能是（　　）

A、1 B、2 C、4 D、6

查看试题解析
3. 已知 $- 2 x > 4$ ，则下列不等式一定成立的是（　　）

A、 $x < - 2$ B、 $x < 2$ C、 $x > - 2$ D、 $x > 2$

查看试题解析
4. 我国传统工艺中，油纸伞制作非常巧妙，其中蕴含着数学知识．如图是油纸伞的张开示意图， $A E = A F$ ， $G E = G F$ ，则 $△ A E G ≌ △ A F G$ 的依据是（）

A、SAS B、ASA C、AAS D、SSS

查看试题解析
5. 下列命题中是真命题的是（　　）

A、绝对值相等的两个数相等 B、两个无理数的和仍是无理数 C、同角的补角相等 D、有公共顶点且相等的两个角是对顶角

查看试题解析
6. 已知一次函数 $y = k x + b$ 的图象经过第一，二，三象限，且与x轴交于点（－2，0），则不等式 $k x + b > 0$ 的解是（　　）

A、 $x > - 2$ B、 $x > 2$ C、 $x < - 2$ D、 $x < 2$

查看试题解析
7. 如图，在3×3的正方形网格中，从空白的小正方形中再选择一个涂黑，使得3个涂黑的正方形成轴对称图形，则选择的方法有（　　）

A、3种 B、4种 C、5种 D、6种

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，按以下步骤作图：①以 $B$ 为圆心，任意长为半径作弧，分别交 $B A$ 、 $B C$ 于 $M$ 、 $N$ 两点；②分别以 $M$ 、 $N$ 为圆心，以大于 $\frac{1}{2} M N$ 的长为半径作弧，两弧相交于点 $P$ ；③作射线 $B P$ ，交边 $A C$ 于 $D$ 点.若 $A B = 10$ ， $B C = 6$ ，则线段 $C D$ 的长为（）

A、3 B、 $\frac{10}{3}$ C、 $\frac{8}{3}$ D、 $\frac{16}{5}$

查看试题解析
9. 如图，点A坐标为 $(0 ， - 2)$ ，直线 $y = - \frac{1}{2} x + 3$ 分别交x轴，y轴于点N，M，点B是线段MN上一点，连结AB.现以AB为边，点A为直角顶点构造等腰直角 $△ A B C$ .若点C恰好落在x轴上，则点B的坐标为（　　）

A、 $(1 ， \frac{3}{2})$ B、 $(2 ， 2)$ C、 $(3 ， \frac{9}{2})$ D、 $(4 ， 5)$

查看试题解析
10. 如图， $Δ A B C$ 是边长为2的等边三角形，M是高 $C D$ 上的一个动点，以 $B M$ 为边向上作等边 $Δ B M N$ ，在点M从点C到点D的运动过程中，点N所经过的路径长是（）

A、2 B、 $\frac{π}{2}$ C、 $\frac{\sqrt{3}}{2} π$ D、 $\sqrt{3}$

查看试题解析

二、填空题

11. “x减去1的值是负数”用不等式表示为.

查看试题解析
12. 在平面直角坐标系中，若点 $P (m + 3 ， 3 - m)$ 在y轴上，则m的值是.

查看试题解析
13. 若一次函数 $y = 3 x + 2$ 的图象经过点 $(- 1 ， y_{1})$ ， $(1 ， y_{2})$ ，则 $y_{1}$ $y_{2}$ （填“＞”，“＜”或“＝”）.

查看试题解析
14. 如图，在 $△ A B C$ 中，AE是 $△ A B C$ 的角平分线，D是AE延长线上一点， $D H ⊥ B C$ 于点H.若 $∠ B = 30 °$ ， $∠ C = 50 °$ ，则 $∠ E D H =$ .

查看试题解析
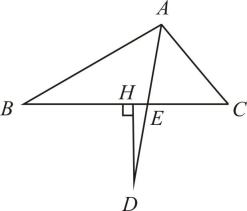15. 如图，已知在四边形ABCD中， $A B ⊥ B C$ ， $D A ⊥ A C$ ， $B C = 3 c m$ ， $A B = 4 c m$ ， $A D = 12 c m$ .若以CD为边，向形外作正 $△ C D E$ ，则 $△ C D E$ 的面积为.

查看试题解析
16. 如图①，在四边形ABCD中，AD∥BC，直线l⊥AB.当直线l沿射线BC方向，从点B开始向右平移时，直线l与四边形ABCD的边分别相交于点E，F.设直线l向右平移的距离为x，线段EF的长y，且y与x的函数关系如图②所示，则四边形ABCD的周长是.

查看试题解析

三、解答题

17. 解不等式组： ${\begin{array}{l} 2 x - 1 < 5 ， \\ \frac{3 x - 1}{2} + 1 \geq x . \end{array}$

查看试题解析
18. 在平面直角坐标系中，点A（1，1），B（4，3），将点A向左平移2个单位长度，再向上平移3个单位长度得到点C.

(1)、在平面直角坐标系中画出△ABC；

(2)、判断△ABC的形状并说明理由.

查看试题解析
19. 如图，在 $△ A B C$ 中， $A B = C B$ ， $∠ A B C = 90 °$ ， F为AB延长线上一点，点E在BC上，且 $B E = B F$ .

(1)、求证： $△ A B E ≌ △ C B F$ ；

(2)、若 $∠ C A E = 20 °$ ，求 $∠ A C F$ 的度数.

查看试题解析
20. 在平面直角坐标系中，一次函数的图象由函数y=x的图象平移得到，且经过点A（1，2）.

(1)、求这个一次函数的解析式；

(2)、若这个一次函数的图象与x轴交于点B，求△AOB的面积.

查看试题解析
21. 已知：如图，在 $△ A B C$ 中，AD是BC边上的高线，CE是AB边上的中线， $D G ⊥ C E$ 于点G， $C D = A E$ .

(1)、求证： $C G = E G$ ；

(2)、若 $A B = 10$ ， $D G = 3$ ，求CE的长.

查看试题解析
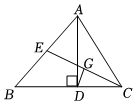22. 在一次机器猫抓机器鼠的展演测试中，鼠先从起点出发，1min后，猫从同一起点出发去追鼠，抓住鼠并稍作停留后，猫抓着鼠沿原路返回.鼠，猫距起点的距离 $y (m)$ 与时间 $x (m i n)$ 之间的关系如图所示.

(1)、在猫追鼠的过程中，猫的平均速度与鼠的平均速度的差是m/min；

(2)、求直线AB的函数表达式；

(3)、求猫返回过程中的平均速度.

查看试题解析
23. 如图，直线 $y = - \frac{4}{3} x + 8$ 与x轴，y轴分别交于A，B两点，点C的坐标为 $(- 6 ， 0)$ ，连接BC，过点О作 $O D ⊥ A B$ 于点D，点Q为线段BC上一个动点.

(1)、求BC，OD的长；

(2)、在线段BO上是否存在一点P，使得 $△ B P Q$ 与 $△ A D O$ 全等？若存在，请求出点P的坐标；若不存在，请说明理由；

(3)、当点C关于OQ的对称点恰好落在 $△ O B D$ 的边上，请直接写出点Q的坐标.

查看试题解析
24. 数学课上，老师在黑板上展示了如下一道探究题：
在 $△ A B C$ 中， $A B = A C = m$ ， $∠ B A C = α$ ，点D，E分别在边AC，AB上，且 $C E = B D$ ，试探究线段AE和线段AD的数量关系.

(1)、初步尝试
如图①，若 $α = 90 °$ ，请探究AE和AD的数量关系，并说明理由.

(2)、类比探究
如图②，若 $α = 120 °$ ，小组讨论后，有小组利用120°的角作垂线构造直角三角形，通过证明两次三角形全等，得到AE和AD的数量关系仍然成立，请你写出推理过程；

(3)、延伸拓展
如图③，将第（2）中的“点E在边AB上”改为“点E在边BA的延长线上”，其它条件不变，请探究AE和AD的数量关系（用含m的式子表示），并说明理由.

查看试题解析