浙江省湖州市德清县2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-11-16 类型:期末考试
一、单选题
-
1. 下面四个图形分别是节能、节水、低碳和绿色食品标志,在这四个标志中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,在△ABC中,AC边上的高线是( )
2. 如图,在△ABC中,AC边上的高线是( ) A、线段DA B、线段BA C、线段BC D、线段BD3. 在下列长度的四根木棒中,能与6cm,9cm长的两根木棒钉成一个三角形的是( )A、1cm B、2cm C、3cm D、4cm4. 若a>b,则下列式子正确的是( )A、b+2>a-2 B、-2017a>-2017b C、4-a>4-b D、5. 在平面直角坐标系中,点 与点 关于 轴对称,则( )A、 , B、 , C、 , D、 ,6. 已知点(﹣1,y1),(4,y2)在一次函数y=3x+a的图象上,则y1 , y2的大小关系是( )A、y1<y2 B、y1=y2 C、y1>y2 D、不能确定7. 能说明命题“若x2≥9,则x≥3”为假命题的一个反例可以是( )A、x=4 B、x=2 C、x=﹣4 D、x=﹣28. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( )
A、线段DA B、线段BA C、线段BC D、线段BD3. 在下列长度的四根木棒中,能与6cm,9cm长的两根木棒钉成一个三角形的是( )A、1cm B、2cm C、3cm D、4cm4. 若a>b,则下列式子正确的是( )A、b+2>a-2 B、-2017a>-2017b C、4-a>4-b D、5. 在平面直角坐标系中,点 与点 关于 轴对称,则( )A、 , B、 , C、 , D、 ,6. 已知点(﹣1,y1),(4,y2)在一次函数y=3x+a的图象上,则y1 , y2的大小关系是( )A、y1<y2 B、y1=y2 C、y1>y2 D、不能确定7. 能说明命题“若x2≥9,则x≥3”为假命题的一个反例可以是( )A、x=4 B、x=2 C、x=﹣4 D、x=﹣28. 如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是( ) A、
A、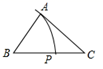 B、
B、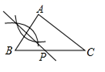 C、
C、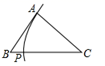 D、
D、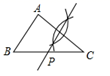 9. 如图, , 两点在正方形网格的格点上,每个方格都是边长为1的正方形,点 也在格点上,且 为等腰三角形,在图中所有符合条件的点 的个数为( )
9. 如图, , 两点在正方形网格的格点上,每个方格都是边长为1的正方形,点 也在格点上,且 为等腰三角形,在图中所有符合条件的点 的个数为( )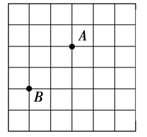 A、7 B、8 C、9 D、1010. 如图,在平面直角坐标系中,点A的坐标为(4,0),点Q是直线yx上的一个动点,以AQ为边,在AQ的右侧作等边△APQ,使得点P落在第一象限,连接OP,则OP+AP的最小值为( )
A、7 B、8 C、9 D、1010. 如图,在平面直角坐标系中,点A的坐标为(4,0),点Q是直线yx上的一个动点,以AQ为边,在AQ的右侧作等边△APQ,使得点P落在第一象限,连接OP,则OP+AP的最小值为( ) A、6 B、4 C、8 D、6
A、6 B、4 C、8 D、6二、填空题
-
11. 命题“内错角相等,两直线平行”的题设是.12. 已知点A的坐标为(3,4),将其向右平移2个单位后的坐标为 .13. 如图,直线经过点和点 , 直线经过点A,则不等式的解集为;
 14. 如图,四边形ABCD中,∠ABC=∠CDA=90°,分别以它的四条边为斜边,向外作等腰直角三角形,其中3个三角形面积分别为2,5,9,则第4个三角形面积为
14. 如图,四边形ABCD中,∠ABC=∠CDA=90°,分别以它的四条边为斜边,向外作等腰直角三角形,其中3个三角形面积分别为2,5,9,则第4个三角形面积为 15.
15.已知平面直角坐标系中,O为坐标原点,点A坐标为(0,8),点B坐标为(4,0),点E是直线y=x+4上的一个动点,若∠EAB=∠ABO,则点E的坐标为
 16. 如图,在△ABC中,AB>AC,∠B=45°,AC=5,BC=4 , E是AB边上一点,将△BEC沿EC所在直线翻折得到△DEC,DC交AB于F,当DE∥AC时,BE的长为 .
16. 如图,在△ABC中,AB>AC,∠B=45°,AC=5,BC=4 , E是AB边上一点,将△BEC沿EC所在直线翻折得到△DEC,DC交AB于F,当DE∥AC时,BE的长为 .
三、解答题
-
17. 如图,已知AC平分∠BAD,AB=AD.求证:∠B=∠D.
 18. 解不等式组:19. 如图所示的象棋棋盘上,若帅位于点(1,0)上,相位于点(3,0)上.
18. 解不等式组:19. 如图所示的象棋棋盘上,若帅位于点(1,0)上,相位于点(3,0)上.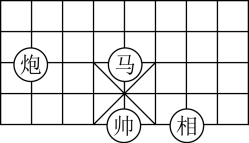 (1)、请在如图所示的网格中建立平面直角坐标系;(2)、炮所在点的坐标是 , 马与帅的距离是;(3)、若要把炮移动到与它关于y轴对称的点的位置,则移动后炮的位置是(用坐标表示).20. 如图,一次函数y=-2x+4的图象分别与x轴、y轴交于点A,B.
(1)、请在如图所示的网格中建立平面直角坐标系;(2)、炮所在点的坐标是 , 马与帅的距离是;(3)、若要把炮移动到与它关于y轴对称的点的位置,则移动后炮的位置是(用坐标表示).20. 如图,一次函数y=-2x+4的图象分别与x轴、y轴交于点A,B.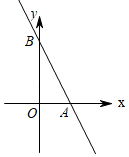 (1)、求△AOB的面积;(2)、在该一次函数图象上有一点P到x轴的距离为6,求点P的坐标.21. 防疫期间,某公司购买 两种不同品牌的免洗洗手液,若购买A种10件, 种5件,共需130元;若购A种5件, 种10件,共需140元.(1)、 两种洗手液每件各多少元?(2)、若购买 两种洗手液共100件,且总费用不超过900元,则A种洗手液至少需要购买多少件?22. 甲、乙两人分别从同一公路上的A,B两地同时出发骑车前往C地,两人行驶的路程y(km)与甲行驶的时间x(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题:
(1)、求△AOB的面积;(2)、在该一次函数图象上有一点P到x轴的距离为6,求点P的坐标.21. 防疫期间,某公司购买 两种不同品牌的免洗洗手液,若购买A种10件, 种5件,共需130元;若购A种5件, 种10件,共需140元.(1)、 两种洗手液每件各多少元?(2)、若购买 两种洗手液共100件,且总费用不超过900元,则A种洗手液至少需要购买多少件?22. 甲、乙两人分别从同一公路上的A,B两地同时出发骑车前往C地,两人行驶的路程y(km)与甲行驶的时间x(h)之间的关系如图所示,请根据图象所提供的信息解答下列问题: (1)、A,B两地相距 km;乙骑车的速度是km/h;(2)、请分别求出甲、乙两人在0≤x≤6的时间段内y与x之间的函数关系式;(3)、求甲追上乙时用了多长时间.23. 在△ABC中,∠BAC=90°,AB=AC.
(1)、A,B两地相距 km;乙骑车的速度是km/h;(2)、请分别求出甲、乙两人在0≤x≤6的时间段内y与x之间的函数关系式;(3)、求甲追上乙时用了多长时间.23. 在△ABC中,∠BAC=90°,AB=AC. (1)、如图1,点D是CA延长线上的一点,点E在线段AB上,且AD=AE,连接BD和CE,延长CE交BD于点F.求证:BD=CE;(2)、在(1)的条件下,若点F为BD的中点,求∠AFD的度数;(3)、如图2,点P是△ABC外一点,∠APB=45°,猜想PA,PB,PC三条线段长度之间存在的数量关系,并证明你的结论.24. 如图,在平面直角坐标系中,直线y=kx+b分别交x轴,y轴于点A(6,0),点B(0,-8),过点D(0,16)作平行于x轴的直线CD,交AB于点C,点E(0,m)在线段OD上,延长CE交x轴于点F,点G在x轴的正半轴上,且AG=AF.
(1)、如图1,点D是CA延长线上的一点,点E在线段AB上,且AD=AE,连接BD和CE,延长CE交BD于点F.求证:BD=CE;(2)、在(1)的条件下,若点F为BD的中点,求∠AFD的度数;(3)、如图2,点P是△ABC外一点,∠APB=45°,猜想PA,PB,PC三条线段长度之间存在的数量关系,并证明你的结论.24. 如图,在平面直角坐标系中,直线y=kx+b分别交x轴,y轴于点A(6,0),点B(0,-8),过点D(0,16)作平行于x轴的直线CD,交AB于点C,点E(0,m)在线段OD上,延长CE交x轴于点F,点G在x轴的正半轴上,且AG=AF. (1)、求直线AB的函数表达式;(2)、当点E恰好是OD的中点时,求△ACG的面积;(3)、是否存在m,使得△FCG是直角三角形?若存在,求m的值;若不存在,请说明理由.
(1)、求直线AB的函数表达式;(2)、当点E恰好是OD的中点时,求△ACG的面积;(3)、是否存在m,使得△FCG是直角三角形?若存在,求m的值;若不存在,请说明理由.