浙江省杭州市萧山区2021-2022学年八年级上学期期末数学试题
试卷更新日期:2022-11-16 类型:期末考试
一、单选题
-
1. 下列各组图形中是全等三角形的一组是( )A、
 B、
B、 C、
C、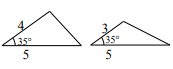 D、
D、 2. 下列语句中是命题的有( )
2. 下列语句中是命题的有( )①线段垂直平分线上的点到线段两端的距离相等;
②作点A关于直线l的对称点
③三边对应相等的两个三角形全等吗?
④角平分线上的点到角两边的距离相等.
A、1个 B、2个 C、3个 D、4个3. 已知下列式子中成立的是( )A、 B、 C、 D、4. 下列尺规作图分别表示:①作一个角的平分线;②作一个角等于已知角;③作一条线段的垂直平分线.其中作法正确的是( )
① ② ③
A、①② B、①③ C、②③ D、①②③5. 一次函数 的图像经过( )A、第一、二、三象限 B、第一、三、四象限 C、第二、三、四象限 D、第一、二、四象限6. 在平面直角坐标系中,点P(-3,6)所在象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 如图,在Rt△ABC中,∠ACB是直角,点D是AB边上的中点,下列成立的有( )①∠A+∠B=90° ②AC2+BC2=AB2 ③2CD=AB ④∠B= 30°
 A、①②④ B、①③ C、②④ D、①②③8. 检测游泳池的水质,要求三次检验的pH的平均值不小于7.2,且不大于7.8.前两次检验,pH的读数分别是7.4,7.9,那么第三次检验的pH应该为多少才能合格?设第3次的pH值为x,由题意可得( )A、 B、 C、 D、9. 如图,在△ABC中,AB=BC,AD⊥BC于点D,CE平分∠ACB交AB于点E,交AD于点P,若∠B=x°,则∠APE的度数为( )
A、①②④ B、①③ C、②④ D、①②③8. 检测游泳池的水质,要求三次检验的pH的平均值不小于7.2,且不大于7.8.前两次检验,pH的读数分别是7.4,7.9,那么第三次检验的pH应该为多少才能合格?设第3次的pH值为x,由题意可得( )A、 B、 C、 D、9. 如图,在△ABC中,AB=BC,AD⊥BC于点D,CE平分∠ACB交AB于点E,交AD于点P,若∠B=x°,则∠APE的度数为( ) A、 B、 C、 D、10. 已知等边△ABC的边长为12,D是AB上的动点,过D作DE⊥BC于点E,过E作EF⊥AC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( )
A、 B、 C、 D、10. 已知等边△ABC的边长为12,D是AB上的动点,过D作DE⊥BC于点E,过E作EF⊥AC于点F,过F作FG⊥AB于点G.当G与D重合时,AD的长是( ) A、9 B、8 C、4 D、3
A、9 B、8 C、4 D、3二、填空题
-
11. 正比例函数y=3x的比例系数是 .12. “等腰三角形底边上的高线与中线互相重合”的逆命题是 . 这个逆命题是命题.(真、假)13. 不等式 的最小负整数解.14. 如图,一次函数的图象与x轴交于点A(3,0),与y轴交于点B(0,4),与正比例函数的图象交于点C,且点C的横坐标为2,则不等式的解集为.
 15. 已知A,B两地相距80km,甲、乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲、乙离开A地的路程s(km)与时间(h)的函数关系的图象,则甲与乙的速度之差为 , 甲出发后经过小时追上乙.
15. 已知A,B两地相距80km,甲、乙两人沿同一条公路从A地出发到B地,乙骑自行车,甲骑摩托车.图中DE,OC分别表示甲、乙离开A地的路程s(km)与时间(h)的函数关系的图象,则甲与乙的速度之差为 , 甲出发后经过小时追上乙.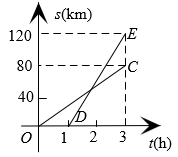 16. 如图,在中, , D为BC的中点,连接AD,E是AB上的一点,P是AD上一点,连接EP、BP, , , 则的最小值是.
16. 如图,在中, , D为BC的中点,连接AD,E是AB上的一点,P是AD上一点,连接EP、BP, , , 则的最小值是.
三、解答题
-
17. 以下是圆圆解不等式组的解答过程:
解:由①,得 , 所以 .
由②,得 , 所以 ,
所以 . 所以原不等式组的解是 .
圆圆的解答过程是否有错误?如果有错误,请写出正确的解答过程.
18. 在① , ② , ③这三个条件中选择其中一个,补充在下面的问题中,并完成问题的解答.
问题:如图,点A、D、B、E在同一条直线上, , , 若 ,
求证:.
19. 已知的三边 , , .(1)、求证:是直角三角形.(2)、利用第(1)题的结论,写出两个直角三角形的边长,要求它们的边长均为正整数.20. 已知函数y=(2m+1)x+m-3.(1)、若函数图象经过原点 , 求m的值; (2)、若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;(3)、若这个函数是一次函数,且图象不经过第四象限,求m的取值范围.21. 如图,在中, , BE平分 , AD为BC边上的高,且 .
, 求m的值; (2)、若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围;(3)、若这个函数是一次函数,且图象不经过第四象限,求m的取值范围.21. 如图,在中, , BE平分 , AD为BC边上的高,且 . (1)、求证:(2)、试判断线段AB与BD,DH之间有何数量关系,并说明理由.22. 某校八年级举行英语演讲比赛,购买A,B两种笔记本作为奖品,这两种笔记本的单价分别是12元和8元.根据比赛设奖情况,需购买笔记本共30本.(1)、设买A笔记本n本,买两种笔记本的总费为w元,写出w(元)关于n(本)的函数关系式;(2)、若所购买A笔记本的数量要不多于B笔记本数量的 ,但又不少于B笔记本数量的 ,购买这两种笔记本各多少时,费用最少?最少的费用是多少元?(3)、若学校根据实际除了A,B两种笔记本外,还需一种单价为10元的C笔记本,若购买的总本数不变,C笔记本的数量是B笔记本的数量的2倍,A笔记本的数量不少于B笔记本的数量,试设计一种符合上述条件购买方案,且使所需费用最少.23.
(1)、求证:(2)、试判断线段AB与BD,DH之间有何数量关系,并说明理由.22. 某校八年级举行英语演讲比赛,购买A,B两种笔记本作为奖品,这两种笔记本的单价分别是12元和8元.根据比赛设奖情况,需购买笔记本共30本.(1)、设买A笔记本n本,买两种笔记本的总费为w元,写出w(元)关于n(本)的函数关系式;(2)、若所购买A笔记本的数量要不多于B笔记本数量的 ,但又不少于B笔记本数量的 ,购买这两种笔记本各多少时,费用最少?最少的费用是多少元?(3)、若学校根据实际除了A,B两种笔记本外,还需一种单价为10元的C笔记本,若购买的总本数不变,C笔记本的数量是B笔记本的数量的2倍,A笔记本的数量不少于B笔记本的数量,试设计一种符合上述条件购买方案,且使所需费用最少.23. (1)、如图①,在中,D为外一点,若AC平分 , 于点E, , 求证:;
(1)、如图①,在中,D为外一点,若AC平分 , 于点E, , 求证:;琮琮同学:我的思路是在AB上取一点F,使得 , 连结CF,先证明≌得到
, 再证明 , 从而得出结论;
宸宸同学:我觉得也可以过点C作边AD的高线CG,由角平分线的性质得出 , 再证明≌ , 从而得出结论.请根据两位同学的思路选择一种写出证明过程.
(2)、如图②,D、E、F分别是等边的边BC、AB,AC上的点,AD平分 , 且.求证:.