2023年春季北师版数学九年级下册第一章 《直角三角形的边角关系》单元检测A
试卷更新日期:2022-11-16 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 如图,从热气球A看一栋楼底部C的俯角是( )
 A、 B、 C、 D、2. 如图,某地修建一座高的天桥,已知天桥斜面的坡度为 , 则斜坡的长度为( )
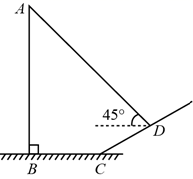
A、 B、 C、 D、2. 如图,某地修建一座高的天桥,已知天桥斜面的坡度为 , 则斜坡的长度为( )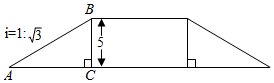 A、 B、 C、 D、3. 如图,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下,在斜坡上的树影BC长为m,则大树AB的高为( )
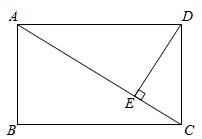
A、 B、 C、 D、3. 如图,坡角为α的斜坡上有一棵垂直于水平地面的大树AB,当太阳光线与水平线成45°角沿斜坡照下,在斜坡上的树影BC长为m,则大树AB的高为( )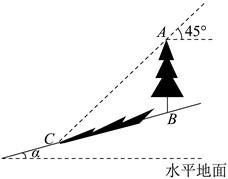 A、 B、 C、 D、4. 如图,在矩形纸片中, , , 将沿折叠到位置,交于点 , 则的值为( )
A、 B、 C、 D、4. 如图,在矩形纸片中, , , 将沿折叠到位置,交于点 , 则的值为( )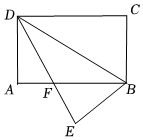 A、 B、 C、 D、5. 如图,已知点B,D,C在同一直线的水平,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β, , 则建筑物AB的高度为( )
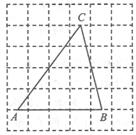
A、 B、 C、 D、5. 如图,已知点B,D,C在同一直线的水平,在点C处测得建筑物AB的顶端A的仰角为α,在点D处测得建筑物AB的顶端A的仰角为β, , 则建筑物AB的高度为( ) A、 B、 C、 D、6. 如图,在正方形方格纸中,每个小正方形的边长都相等,A,B,C,D都在格点处,AB与CD相交于点P,则cos∠APC的值为( )
A、 B、 C、 D、6. 如图,在正方形方格纸中,每个小正方形的边长都相等,A,B,C,D都在格点处,AB与CD相交于点P,则cos∠APC的值为( ) A、 B、 C、 D、7. 如图,在中, , , 点D是AC上一点,连接BD.若 , , 则CD的长为( )
A、 B、 C、 D、7. 如图,在中, , , 点D是AC上一点,连接BD.若 , , 则CD的长为( ) A、 B、3 C、 D、28. 一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m.∠ABC=α.则房顶A离地面EF的高度为( )
A、 B、3 C、 D、28. 一配电房示意图如图所示,它是一个轴对称图形.已知BC=6m.∠ABC=α.则房顶A离地面EF的高度为( )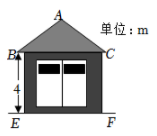 A、 B、 C、 D、9. 矩形纸片中,E为的中点,连接 , 将沿折叠得到 , 连接.若 , , 则的长是( )
A、 B、 C、 D、9. 矩形纸片中,E为的中点,连接 , 将沿折叠得到 , 连接.若 , , 则的长是( )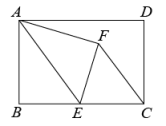 A、3 B、 C、 D、10. 如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )
A、3 B、 C、 D、10. 如图,在平面直角坐标系内有一点P(3,4),连接OP,则OP与x轴正方向所夹锐角α的正弦值是( )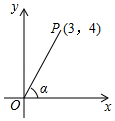 A、 B、 C、 D、
A、 B、 C、 D、二、解答题(共9题,共72分)
-
11. 计算:12. 计算:.13. 2022年北京冬奥会的成功举办激发了人们对冰雪运动的热情.如图是某滑雪场的横截面示意图,雪道分为AB,BC两部分,小明同学在C点测得雪道BC的坡度i=1:2.4,在A点测得B点的俯角∠DAB=30°.若雪道AB长为270m,雪道BC长为260m.
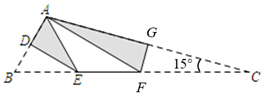
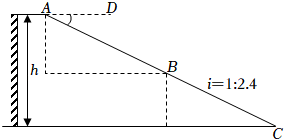 (1)、求该滑雪场的高度h;(2)、据了解,该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求,其中甲设备每小时造雪量比乙设备少35m3 , 且甲设备造雪150m3所用的时间与乙设备造雪500m3所用的时间相等.求甲、乙两种设备每小时的造雪量.14. 如图所示,九(1)班数学兴趣小组为了测量河对岸的古树A、B之间的距离,他们在河边与AB平行的直线l上取相距60m的C、D两点,测得∠ACB=15°,∠BCD=120°,∠ADC=30°.
(1)、求该滑雪场的高度h;(2)、据了解,该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求,其中甲设备每小时造雪量比乙设备少35m3 , 且甲设备造雪150m3所用的时间与乙设备造雪500m3所用的时间相等.求甲、乙两种设备每小时的造雪量.14. 如图所示,九(1)班数学兴趣小组为了测量河对岸的古树A、B之间的距离,他们在河边与AB平行的直线l上取相距60m的C、D两点,测得∠ACB=15°,∠BCD=120°,∠ADC=30°.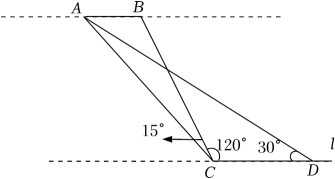 (1)、求河的宽度;(2)、求古树A、B之间的距离.(结果保留根号)15. 如图,已知四边形ABCD为矩形 , ,点E在BC上, ,将△ABC沿AC翻折到△AFC,连接EF.
(1)、求河的宽度;(2)、求古树A、B之间的距离.(结果保留根号)15. 如图,已知四边形ABCD为矩形 , ,点E在BC上, ,将△ABC沿AC翻折到△AFC,连接EF. (1)、求EF的长;(2)、求sin∠CEF的值.16. 如图1所示,某登山运动爱好者由山坡①的山顶点A处沿线段至山谷点处,再从点处沿线段至山坡②的山顶点处.如图2所示,将直线视为水平面,山坡①的坡角 , 其高度为0.6千米,山坡②的坡度 , 于 , 且千米.
(1)、求EF的长;(2)、求sin∠CEF的值.16. 如图1所示,某登山运动爱好者由山坡①的山顶点A处沿线段至山谷点处,再从点处沿线段至山坡②的山顶点处.如图2所示,将直线视为水平面,山坡①的坡角 , 其高度为0.6千米,山坡②的坡度 , 于 , 且千米.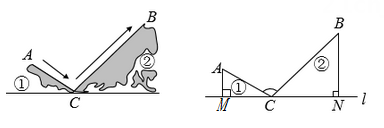 (1)、求的度数;(2)、求在此过程中该登山运动爱好者走过的路程.17. 圭表(如图1)是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标竿(称为“表”)和一把呈南北方向水平固定摆放的与标竿垂直的长尺(称为“圭”),当正午太阳照射在表上时,日影便会投影在圭面上,圭面上日影长度最长的那一天定为冬至,日影长度最短的那一天定为夏至.图2是一个根据某市地理位置设计的圭表平面示意图,表 AC垂直圭BC,已知该市冬至正午太阳高度角(即∠ABC)为37° ,夏至正午太阳高度角(即∠ADC)为84°,圭面上冬至线与夏至线之间的距离(即DB的长)为4米.
(1)、求的度数;(2)、求在此过程中该登山运动爱好者走过的路程.17. 圭表(如图1)是我国古代一种通过测量正午日影长度来推定节气的天文仪器,它包括一根直立的标竿(称为“表”)和一把呈南北方向水平固定摆放的与标竿垂直的长尺(称为“圭”),当正午太阳照射在表上时,日影便会投影在圭面上,圭面上日影长度最长的那一天定为冬至,日影长度最短的那一天定为夏至.图2是一个根据某市地理位置设计的圭表平面示意图,表 AC垂直圭BC,已知该市冬至正午太阳高度角(即∠ABC)为37° ,夏至正午太阳高度角(即∠ADC)为84°,圭面上冬至线与夏至线之间的距离(即DB的长)为4米. (1)、求∠BAD的度数.(2)、求表AC的长(最后结果精确到0.1米).
(1)、求∠BAD的度数.(2)、求表AC的长(最后结果精确到0.1米).(参考数据:sin37°≈ ,cos37°≈ ,tan37°≈ ,tan84°≈ )
18. 小华将一张纸对折后做成的纸飞机如图1,纸飞机机尾的横截面是一个轴对称图形,其示意图如图2,已知AD=BE=10cm,CD=CE=5cm,AD⊥CD,BE⊥CE,∠DCE=40°.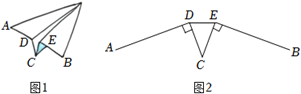 (1)、连结DE,求线段DE的长.(2)、求点A,B之间的距离.
(1)、连结DE,求线段DE的长.(2)、求点A,B之间的距离.(结果精确到0.1cm.参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)
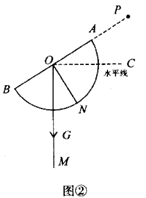
19. 某数学兴趣小组自制测角仪到公园进行实地测量,活动过程如下:(1)、探究原理制作测角仪时,将细线一段固定在量角器圆心 处,另一端系小重物 .测量时,使支杆 、量角器90°刻度线 与铅垂线 相互重合(如图①),绕点 转动量角器,使观测目标 与直径两端点 共线(如图②),此目标 的仰角 .请说明两个角相等的理由.
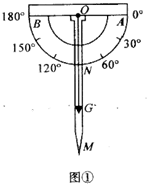
 (2)、实地测量
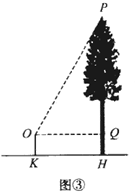
(2)、实地测量如图③,公园广场上有一棵树,为了测量树高,同学们在观测点 处测得顶端 的仰角 ,观测点与树的距离 为5米,点 到地面的距离 为1.5米;求树高 . ( ,结果精确到0.1米)
 (3)、拓展探究
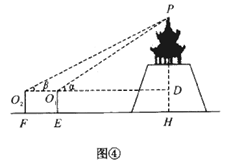
(3)、拓展探究公园高台上有一凉亭,为测量凉亭顶端 距离地面高度 (如图④),同学们讨论,决定先在水平地面上选取观测点 ( 在同一直线上),分别测得点 的仰角 ,再测得 间的距离 ,点 到地面的距离 均为1.5米;求 (用 表示).
三、填空题(每题3分,共18分)
-
20. 阅读材料:余弦定理是描述三角形中三边长度与一个角余弦值关系的数学定理,运用它可以解决一类已知三角形两边及夹角求第三边或者已知三边求角的问题.余弦定理是这样描述的:在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,则三角形中任意一边的平方等于另外两边的平方和减去这两边及这两边的夹角的余弦值的乘积的2倍.
用公式可描述为:a2=b2+c2﹣2bccosA
b2=a2+c2﹣2accosB
c2=a2+b2﹣2abcosC
现已知在△ABC中,AB=3,AC=4,∠A=60°,则BC= .
21. 如图,直角三角形 纸片中, ,点 是 边上的中点,连接 ,将 沿 折叠,点 落在点 处,此时恰好有 .若 ,那么 .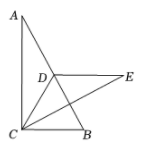 22. 如图,在 正方形网格中, 的顶点 、 、 都在网格线上,且都是小正方形边的中点,则 .
22. 如图,在 正方形网格中, 的顶点 、 、 都在网格线上,且都是小正方形边的中点,则 .