河南省信阳市普通高中2022-2023学年高三上学期理数第一次教学质量检测试卷
试卷更新日期:2022-11-15 类型:高考模拟
一、单选题
-
1. 设集合 , 集合 , 则集合等于( )A、1 B、 C、 D、2. “”是“在上恒成立”的( )A、充分而不必要条件 B、必要而不充分条件 C、充分必要条件 D、既不充分也不必要条件3. 已知命题“存在 , 使等式成立”是假命题,则实数的取值范围( )A、 B、 C、 D、4. 函数在区间的图象大致为( )A、
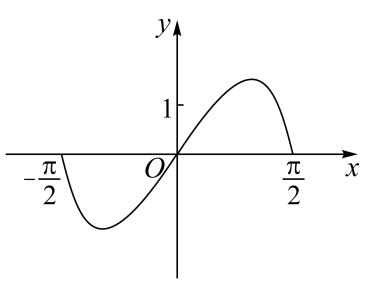 B、
B、 C、
C、 D、
D、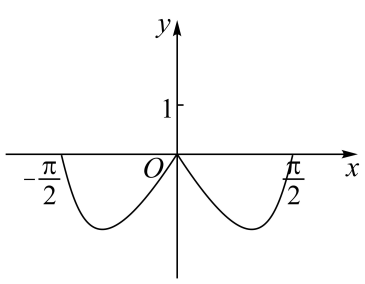 5. 已知角终边所在直线的斜率为 , 则( )A、 B、5 C、 D、6. 为加强环境保护,治理空气污染,某环保部门对辖区内一工厂产生的废气进行了监测,发现该厂产生的废气经过过滤后排放,过滤过程中废气的污染物数量 与时间 的关系为 .如果在前5个小时消除了 的污染物,那么污染物减少 需要花的时间为( )A、7小时 B、10小时 C、15小时 D、18小时7. 已知定义在上的偶函数满足 , 若 , 则( )A、 B、 C、 D、8. 已知函数 的部分图象如图所示,下列说法正确的是( )
5. 已知角终边所在直线的斜率为 , 则( )A、 B、5 C、 D、6. 为加强环境保护,治理空气污染,某环保部门对辖区内一工厂产生的废气进行了监测,发现该厂产生的废气经过过滤后排放,过滤过程中废气的污染物数量 与时间 的关系为 .如果在前5个小时消除了 的污染物,那么污染物减少 需要花的时间为( )A、7小时 B、10小时 C、15小时 D、18小时7. 已知定义在上的偶函数满足 , 若 , 则( )A、 B、 C、 D、8. 已知函数 的部分图象如图所示,下列说法正确的是( )
①函数 的图象关于点 对称②函数 的图象关于直线 对称③函数 在 单调递减④该图象向右平移 个单位可得 的图象
A、①② B、①③ C、①②③ D、①②④9. 已知函数在上单调递减,则实数的取值范围( )A、 B、 C、 D、10. 已知函数 , 若在区间上单调递减,则实数的取值范围( )A、 B、 C、 D、11. 已知实数 ,且 , , ,则( )A、 B、 C、 D、12. 已知函数及其导函数的定义域都为实数集,记若恒有成立,则正确结论共有( )
(1);(2);(3);(4).A、(1)(3) B、(2)(3) C、(1)(2)(4) D、(2)(3)(4)二、填空题
-
13. 已知函数的图象在点处的切线方程是 , 则.14. 已知直线分别与函数和的图象交于点 , , 则 .15. 如图是某商业小区的平面设计图,初步设计该小区为半径是200米,圆心角是120°的扇形 . 为南门位置, 为东门位置,小区里有一条平行于 的小路 ,若 米,则圆弧 的长为米
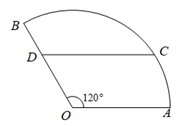 16. 已知 , 函数的最小值为 , 则的取值范围是:.
16. 已知 , 函数的最小值为 , 则的取值范围是:.三、解答题
-
17. 已知 , 设: , 成立;: , 成立,如果“”为真,“”为假,求实数的取值范围.18. 已知函数是偶函数.(1)、求实数的值;(2)、设 , 若函数与的图象有且仅有一个公共点, 求实数的取值范围.19. 在锐角△ABC中,角A,B,C的对边分别为a,b,c,且 .(1)、求角B的大小;(2)、求cosA+cosB+cosC的取值范围.20. 设函数.(1)、若在上存在单调递增区间,求的取值范围;(2)、当时,在上的最小值为 , 求在该区间上的最大值.
