广东省2023年普通高中数学学业水平合格性考试模拟（二）试题

试卷更新日期：2022-11-15 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {1 ， 2 ， 3 ， 4}$ ， $B = {x | x^{2} - 3 < 0}$ ，则 $A ∩ B =$ （）

A、 ${1}$ B、 ${1 ， 2}$ C、 ${1 ， 2 ， 3}$ D、 ${1 ， 2 ， 3 ， 4}$

查看试题解析
2. 下列运算错误的是（）

A、a³+a³=2a⁶ B、a⁶÷a^-3=a⁹ C、a³·a³=a⁶ D、（-2a²）³=-8a⁶

查看试题解析
3. 已知 $\sin 2 α > 0$ ，则（）

A、 $\tan α > 0$ B、 $\sin α > 0$ C、 $\cos α > 0$ D、 $\cos 2 α > 0$

查看试题解析
4. 在四边形ABCD中，给出下列四个结论，其中一定正确的是（）

A、 $\vec{A B} + \vec{B C} = \vec{C A}$ B、 $\vec{A B} - \vec{A D} = \vec{B D}$ C、 $\vec{A B} + \vec{A D} = \vec{A C}$ D、 $\vec{B C} + \vec{C D} = \vec{B D}$

查看试题解析
5. 已知100个数据的第75百分位数是9.3，则下列说法正确的是（）

A、这100个数据中一定有75个数小于或等于9.3 B、把这100个数据从小到大排列后，9.3是第75个数据 C、把这100个数据从小到大排列后，9.3是第75个与第76个数据的平均数 D、把这100个数据从小到大排列后，9.3是第75个与第74个数据的平均数

查看试题解析
6. 从一箱产品中随机地抽取一件，设事件 $A =$ {抽到一等品}，事件 $B =$ {抽到二等品}，事件 $C =$ {抽到三等品}，且已知 $P (A) = 0.65$ ， $P (B) = 0.2$ ， $P (C) = 0.1$ ，则事件“抽到的产品不是一等品”的概率为（）

A、 $0.2$ B、 $0.35$ C、 $0.5$ D、 $0.4$

查看试题解析
7. 在区间(0，＋∞)上不是增函数的函数是（）

A、 $y = 2 x + 1$ B、 $y = 3 x^{2} + 1$ C、 $y = \frac{2}{x}$ D、 $y = 2 x^{2} + x + 1$

查看试题解析
8. 正方体ABCD－A₁B₁C₁D₁中与AD₁垂直的平面是(　　)

A、平面DD₁C₁C B、平面A₁DB₁ C、平面A₁B₁C₁D₁ D、平面A₁DB

查看试题解析
9. 某商场在今年端午节的促销活动中，对6月9日时至14时的销售额进行统计，其频率分布直方图如图所示，已知9时至10时的销售额为3万元，则11时至12时的销售额为（）

A、 $8$ 万元 B、 $10$ 万元 C、 $12$ 万元 D、 $15$ 万元

查看试题解析
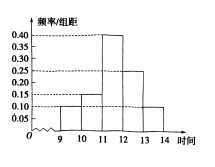10. “ $x > 1$ ”是“ $l o g_{\frac{1}{2}} (x + 2) < 0$ ”的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分又不必要条件

查看试题解析
11. 若函数 $f (x) = s i n (x + φ)$ 是偶函数，则 $φ$ 可取一个值为（）

A、 $- π$ B、 $- \frac{π}{2}$ C、 $\frac{π}{4}$ D、 $2 π$

查看试题解析
12. 若a>0，b>0，a＋2b＝5，则ab的最大值为（）

A、25 B、 $\frac{25}{2}$ C、 $\frac{25}{4}$ D、 $\frac{25}{8}$

查看试题解析
13. 幂函数y=f（x）的图象过点（4，2），则幂函数y=f（x）的图象是（）

A、 B、 C、 D、

查看试题解析
14. 在△ABC中，角 $A ， B ， C$ 的对边分别是 $a ， b ， c$ ，若 $a = \frac{\sqrt{5}}{2} b$ ， $A = 2 B$ ，则 $\cos B =$ （）

A、 $\frac{\sqrt{5}}{3}$ B、 $\frac{\sqrt{5}}{4}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{\sqrt{5}}{6}$

查看试题解析
15. 从一批产品中取出三件，设 $A =$ “三件产品全不是次品”， $B =$ “三件产品全是次品”， $C =$ “三件产品不全是次品”，则下列结论正确的是（）.

A、A与C互斥 B、B与C互斥 C、任两个均互斥 D、任两个均不互斥

查看试题解析

二、填空题

16. 已知向量 $\vec{a}$ 与 $\vec{b}$ 的夹角为60°，| $\vec{a}$ |=2，| $\vec{b}$ |=1，则| $\vec{a}$ +2 $\vec{b}$ |= .

查看试题解析
17. 函数f（x）=x²-2（a-1）x+2在区间 $(- \infty ， 1]$ 上是减函数，则实数a的范围是

查看试题解析
18. 若轴截面为正方形的圆柱的侧面积是 $4 π$ ，则圆柱的体积为．

查看试题解析
19. 在 $Δ A B C$ 中，角 $A ， B ， C$ 的对边分别为 $a ， b ， c$ .若 $c^{2} = {(a + b)}^{2} - 4 ， C = \frac{2 π}{3}$ ，则 $Δ A B C$ 的面积为.

查看试题解析

三、解答题

20. 某班有男生27名，女生18名，用分层抽样的方法从该班中抽取5名学生去敬老院参加献爱心活动.

(1)、求从该班男生、女生中分别抽取的人数；

(2)、为协助敬老院做好卫生清扫工作，从参加活动的5名学生中随机抽取2名，求这2名学生均为女生的概率.

查看试题解析
21. 已知函数 $f (x) = \sqrt{3} s i n 2 x - c o s 2 x$ .

(1)、求函数f（x）的最小正周期和最大值；

(2)、求函数f（x）的单调递减区间.

查看试题解析
22. 已知 $R t △ A B C$ 的斜边为AB，过点A作PA⊥平面ABC，AM⊥PB于M，AN⊥PC于N.求证：

(1)、BC⊥平面PAC；

(2)、PB⊥平面AMN.

查看试题解析