四川省南充市蓬安县2022-2023学年九年级上学期期中数学试题
试卷更新日期:2022-11-15 类型:期中考试
一、单选题
-
1. 下列计算结果是9的是( )A、 B、 C、 D、2. 下列计算结果正确的是( )A、 B、 C、 D、3. 不等式的解集为( )A、 B、 C、 D、4. 方程的解是( )A、2和-1 B、-2和1 C、-2和-1 D、2和15. 若某银行经过两次降息,使三年期存款的年利率由4%降至3.24%,则平均每次降息的百分比是( )A、10% B、9% C、8% D、7%6. 把函数的图像经过平移或旋转后,能与下列函数( )的图像重合A、 B、 C、 D、7. 若方程有两个相等的实数解,则下列方程中无实数解的是( )A、 B、 C、 D、8. 把抛物线向右平移3个单位长度,再向下平移5个单位长度,得到的抛物线是( )A、 B、 C、 D、9. 当时,和大致图像可能是( )A、
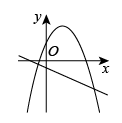 B、
B、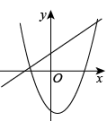 C、
C、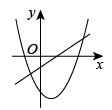 D、
D、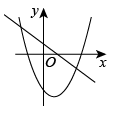 10. 把函数的图象关于直线对称后为函数( )的图象A、 B、 C、 D、
10. 把函数的图象关于直线对称后为函数( )的图象A、 B、 C、 D、二、填空题
-
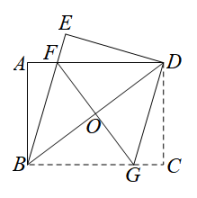
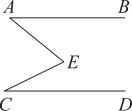
11. 如图, , 若 , , 则∠E= .
 12. 如果关于x的一元二次方程的一个根为3,那么此方程的另一个根为 .13. 由的图象知:当x满足条件时, .14. 已知x+ =5,那么x2+ = .15. 若的值为整数,则正整数a的值为 .16. 关于抛物线 , 给出下列结论:
12. 如果关于x的一元二次方程的一个根为3,那么此方程的另一个根为 .13. 由的图象知:当x满足条件时, .14. 已知x+ =5,那么x2+ = .15. 若的值为整数,则正整数a的值为 .16. 关于抛物线 , 给出下列结论:①当时,抛物线与直线没有交点;
②当时,抛物线与x轴的交点分居在原点的两侧;
③若抛物线在x轴的下方,则a的取值范围为 .
其中正确结论的序号为 .
三、解答题
-
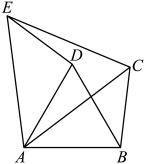
17. 解方程(1)、(2)、18. 指出抛物线的开口方向:写出抛物线的顶点坐标、对称轴方程;当x满足什么条件时,y随x的增大而增大大?当x满足什么条件时,y取最小值多少?当x满足什么条件时,?当x满足什么条件时,?19. 在中,以AB为边作等边 , 以AC为边作等边 , 连接 , 求证: .
 20. 已知方程 .(1)、判断此方程是否有实数根,有几个实数根?(2)、设此方程的两实数根为、 , 且 , 求m的值.21. 过点的直线l与正比例函数的图象交于点、与x轴交于点C.
20. 已知方程 .(1)、判断此方程是否有实数根,有几个实数根?(2)、设此方程的两实数根为、 , 且 , 求m的值.21. 过点的直线l与正比例函数的图象交于点、与x轴交于点C.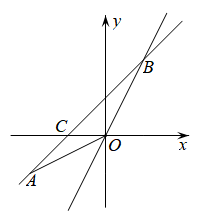 (1)、求直线l、正比例函数的解析式和点C的坐标;(2)、求的面积.22. 以的速度在平地上将一小铁球沿与地面成角的方向击出时,小铁球的飞行路线是一条抛物线.如果不考虑空气的阻力,那么小铁球的飞行高度h(单位:米)与飞行时间t(单位:秒)之间的函数关系是: .(1)、小铁球飞行几秒时,小铁球的高度是25米?(2)、小铁球的飞行高度能否达到45米,若能,需要多少飞行时间?(3)、小铁球在空中飞行了多少时间?23. 某服装店销售A、B两种服装,它们的进价和售价如下表,若老板进A种服装20套和B种服装30套,则需资金18000元;若老板进A种服装30套和B种服装40套,则需要资金25000元.
(1)、求直线l、正比例函数的解析式和点C的坐标;(2)、求的面积.22. 以的速度在平地上将一小铁球沿与地面成角的方向击出时,小铁球的飞行路线是一条抛物线.如果不考虑空气的阻力,那么小铁球的飞行高度h(单位:米)与飞行时间t(单位:秒)之间的函数关系是: .(1)、小铁球飞行几秒时,小铁球的高度是25米?(2)、小铁球的飞行高度能否达到45米,若能,需要多少飞行时间?(3)、小铁球在空中飞行了多少时间?23. 某服装店销售A、B两种服装,它们的进价和售价如下表,若老板进A种服装20套和B种服装30套,则需资金18000元;若老板进A种服装30套和B种服装40套,则需要资金25000元.种类
A
B
进价(元/套)
a
b
售价(元/套)
480
660
(1)、求A、B两种衣服每套的进价;(2)、若老板用不超过36000元的资金进A、B两种服装共100套,则老板按售价卖出这100套服装的最大利润是多少?(3)、根据市场情况,老板在11月份按售价可卖A种服装14套.假设老板按售价每套A种服装每降价10元,就可多卖出一套A种服装,请问当售价定为多少时,老板在11月份卖A种服装获得的利润最大.