广西壮族自治区桂林市灌阳县2022-2023学年八年级上学期期中数学试题

试卷更新日期：2022-11-15 类型：期中考试

进入出卷网下载

一、单选题

1. 无论a取何值，下列分式总有意义的是（）

A、 $\frac{a - 1}{a^{2} + 1}$ B、 $\frac{a + 1}{a^{2}}$ C、 $\frac{1}{a^{2} - 1}$ D、 $\frac{1}{a + 1}$

查看试题解析
2. 下列式子从左到右的变形一定正确的是（）

A、 $\frac{a m}{b m} = \frac{a}{b}$ B、 $\frac{a}{b} = \frac{a c}{b c}$ C、 $\frac{a}{b} = \frac{a^{2}}{b^{2}}$ D、 $\frac{a}{b} = \frac{a - 1}{b - 1}$

查看试题解析
3. 下列计算正确的是（）

A、 $- a^{8} \div a^{4} = - a^{2}$ B、 $a + a^{2} = a^{3}$ C、 $2 a \cdot 3 a = 6 a$ D、 ${(3 a^{2})}^{3} = 27 a^{6}$

查看试题解析
4. 计算： $x + 1 + \frac{1}{1 - x}$ 正确的是（）

A、 $\frac{2 - x^{2}}{x - 1}$ B、 $\frac{2 x - 1}{x - 1}$ C、 $\frac{x^{2} + 1}{1 - x}$ D、 $\frac{2 - x^{2}}{1 - x}$

查看试题解析
5. 碳纳米管的硬度与金刚石相当，却拥有良好的柔韧性，可以拉伸，我国某物理所研究组已研制出直径为0.0000000005米的碳纳米管，将0.0000000005用科学记数法表示为（）

A、 $0.5 \times 1 0^{- 9}$ B、 $5 \times 1 0^{- 9}$ C、 $0.5 \times 1 0^{- 8}$ D、 $5 \times 1 0^{- 10}$

查看试题解析
6. 若三角形的三边长分别为4、x、7，则x的值可以是（）

A、2 B、3 C、8 D、11

查看试题解析
7. 在测量一个小口圆形容器的壁厚时，小明用“X型转动钳”按如图方法进行测量，其中OA＝OD，OB＝OC，测得AB＝5厘米，EF＝6厘米，圆形容器的壁厚是（）

A、 $0.5$ 厘米 B、6厘米 C、2厘米 D、5厘米

查看试题解析
8. 如图，人字梯中间设计一“拉杆”，在使用梯子时，固定拉杆会增加安全性．这样做蕴含的数学道理是（）

A、三角形具有稳定性 B、两点之间线段最短 C、经过两点有且只有一条直线 D、垂线段最短

查看试题解析
9. 下列命题中，是真命题的是（）

A、同位角相等 B、同旁内角相等，两直线平行 C、若 $a^{2} = b^{2}$ ，则 $a = b$ D、对顶角相等

查看试题解析
10. 等腰三角形的一个底角是40°，则它的顶角是（）

A、100° B、40°或70° C、70° D、40°

查看试题解析
11. 如图，在△ABC中，BC=8cm，AB的垂直平分线交AB于点D，交边AC于点E，△BCE的周长等于18cm，则AC的长等于（）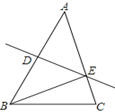

A、8cm B、10cm C、12cm D、14cm

查看试题解析
12. 如图，已知△ABC中，AB＝AC，∠BAC＝90°，直角∠EPF的顶点P是BC中点，两边PE，PF分别交AB，AC于点E，F，当∠EPF在△ABC内绕顶点P旋转时（点E不与A，B重合），以下五个结论正确的个数是（）
①AE＝CF；②∠APE＝∠CPF；③△EPF是等腰直角三角形；④EF＝AP；⑤ $S_{四边形 A E P F} = \frac{1}{2} S_{Δ A B C}$ ．

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

13. 计算 $x^{3} \cdot x^{4} =$ ．

查看试题解析
14. 化简： $\frac{a^{5}}{a^{4}} =$ ．

查看试题解析
15. 等腰三角形的的两边分别为6和3，则它的第三边为．

查看试题解析
16. 已知：如图，AD是△ABC中BC边上的高，∠ABC=42°，AE平分∠BAC，∠ACB=70°，则∠DAE=度．

查看试题解析
17. 如图，D、E、F分别为BC、AD、BE的中点，若△BFD的面积为6，则 △ABC的面积等于.

查看试题解析
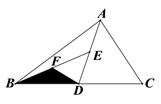18. 如图， $∠ A O B = 60 °$ ，点C是BO延长线时的一点， $O C = 6 c m$ ，动点 $P$ 从点 $C$ 出发沿射线 $C B$ 以 $2 c m / s$ 的速度移动，动点Q从点O出发沿射线 $O A$ 以 $1 c m / s$ 的速度移动，如果点 $P$ 、Q同时出发，用t（s）表示移动的时间，当 $t =$ $s$ 时，△POQ是等边三角形．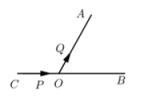

查看试题解析

三、解答题

19. 计算： $| - 7 | + {(- \frac{1}{4})}^{- 1} + (π - 3.14)^{0} - {(\frac{1}{3})}^{- 2}$ ．

查看试题解析
20. 先化简，再求值：（ $\frac{x + 1}{x^{2} - 1}$ + $\frac{x}{x - 1}$ ）÷ $\frac{x + 1}{x^{2} - 2 x + 1}$ ，其中x=2．

查看试题解析
21. 解方程： $\frac{2}{x + 2} + 1 = \frac{x}{x - 1}$ .

查看试题解析
22. 如图，已知 $∠ α$ 和线段c．（不写作法，保留作图痕迹）

(1)、求作 $△ A B C$ ，使 $A C = B C = c$ ， $∠ B = ∠ α$ ；

(2)、作线段 $B C$ 的垂直平分线．

查看试题解析
23. 2014年12月28日“青烟威荣”城际铁路正式开通，从烟台到北京的高铁里程比普快里程缩短了81千米，运行时间减少了9小时，已知烟台到北京的普快列车里程约1026千米，高铁平均时速是普快平均时速的2.5倍．

(1)、求高铁列车的平均时速；

(2)、某日王老师要去距离烟台大约630千米的某市参加14：00召开的会议，如果他买到当日8：40从烟台到该市的高铁票，而且从该市火车站到会议地点最多需要1.5小时．试问在高铁列车准点到达的情况下他能在开会之前赶到吗？

查看试题解析
24. 如图，已知AB=CD，BC=DA，E，F是AC上的两点，且AE=CF.试说明：BF=DE.

查看试题解析
25. 如果记 $y = \frac{x^{2}}{1 + x^{2}} = f (x)$ ，并且 $f (1)$ 表示当 $x = 1$ 时y的值，即 $f (1) = \frac{1^{2}}{1 + 1^{2}} = \frac{1}{2}$ ； $f (\frac{1}{2})$ 表示当 $x = \frac{1}{2}$ 时y的值，即 $f (\frac{1}{2}) = \frac{{(\frac{1}{2})}^{2}}{1 + {(\frac{1}{2})}^{2}} = \frac{1}{5}$ ；…，求 $f (1) + f (2) + f (\frac{1}{2}) + f (3) + f (\frac{1}{3}) + ⋯ + f (n) + f (\frac{1}{n})$ 的值（结果用含n的代数式表示）．

查看试题解析
26. 如图：

(1)、如图1，已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．证明：DE=BD+CE．

(2)、如图2，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC= $α$ ，其中 $α$ 为任意钝角，请问结论DE=BD+CE是否成立？如成立，请你给出证明；若不成立，请说明理由．

查看试题解析