山东省威海市乳山市2022-2023学年八年级上学期期中数学试题

试卷更新日期：2022-11-15 类型：期中考试

进入出卷网下载

一、单选题

1. 我国主要银行的商标设计基本上都融入了中国古代钱币的图案，如图是我国四个银行的商标图案，其中是轴对称图形的有（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析
2. 如图， $A B ∥ D F$ ，且 $A B = D F$ ，添加下列条件，不能判断 $△ A B C ≅ △ F D E$ 的是（）

A、 $A C = E F$ B、 $B E = C D$ C、 $A C ∥ F F$ D、 $∠ A = ∠ F$

查看试题解析
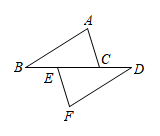3. 如图，为估计池塘两岸 $A ， B$ 间的距离，小明在池塘一侧选取点M，测得 $M A = 15 m$ ， $M B = 11 m$ ，那么 $A B$ 间的距离不可能是（）

A、 $5 m$ B、 $15 m$ C、 $28 m$ D、 $20 m$

查看试题解析
4. 分别以下列各组数据为三角形三边的长度，能构成直角三角形的是（）

A、2，3，4 B、4，5，6 C、7，13，15 D、9，40，41

查看试题解析
5. 小明在平面镜里看到背后墙上电子钟显示的时间如图所示，此刻的实际时间应该是（）

A、21︰05 B、20︰15 C、20︰12 D、21︰50

查看试题解析
6. 如图，将三角板 $D E F$ 的直角放置在 $△ A B C$ 内，恰好三角板的两条直角边分别经过点B，C．若 $∠ A = 55 °$ ，则 $∠ A B D + ∠ A C D$ =（）

A、35 $°$ B、45 $°$ C、55 $°$ D、60 $°$

查看试题解析
7. 如图，将一根长 $20 c m$ 的铅笔放入底面直径为 $9 c m$ ，高为 $12 c m$ 的圆柱形笔筒中，设铅笔露在笔筒外面的长度为 $x c m$ ，则x的最小值是（）

A、5 B、7 C、12 D、13

查看试题解析
8. 如果将长为6cm，宽为5cm的长方形纸片折叠一次，那么这条折痕的长不可能是（）

A、7cm B、5cm C、5.5cm D、8cm

查看试题解析
9. 如图是由单位长度均为1的小正方形组成的网格，A，B，C，D都是网格线的交点，由其中任意三个点连接而成的三角形是直角三角形的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $∠ A = 120 °$ ， $B C = 15$ cm． $A B$ 的垂直平分线交 $A B$ 于点D，交 $B C$ 于点E； $A C$ 的垂直平分线交 $A C$ 于点G，交 $B C$ 于点F． $E F$ 的长为（）

A、3cm B、4cm C、5cm D、6cm

查看试题解析

二、填空题

11. 一个等腰三角形的两边长分别是4和9，则这个等腰三角形的周长是．

查看试题解析
12. 如图，在Rt $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 3$ ， $B C = 4$ ， $A D$ 平分 $∠ C A B$ 交 $B C$ 于D，则 $B D$ = ．

查看试题解析
13. 如图， $A B = A C$ ，点D是 $△ A B C$ 内一点， $∠ D = 110 °$ ， $∠ 1 = ∠ 2$ ，则 $∠ A =$ °．

查看试题解析
14. 如图，是一个两级台阶，它的每一级的长、宽、高分别为 $1.5 m ， 0.3 m ， 0.2 m ，$ A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁从A点沿着台阶面爬到B点的最短路程是m ．

查看试题解析
15. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，点D在直角边 $B C$ 上， $A D$ 平分 $∠ B A C$ ， $D E$ 是 $A B$ 的垂直平分线， $C D = 8 c m$ ，则 $B D$ = $c m$ ．

查看试题解析
16. 图中所示的为“毕达哥拉斯树”的“生长”过程．如图①，一个边长为a的正方形，经过第一次“生长”后在它的上侧长出两个小正方形，且三个正方形所围成的三角形是直角三角形；再经过一次“生长”后变成了图②；如此继续“生长”下去，则第2000次“生长”后，这棵“毕达哥拉斯树”上所有正方形的面积和为．

查看试题解析

三、解答题

17. 如图，将墙面和地平线的一部分分别标记 $E F$ ， $F G$ ，且 $E F ⊥ F G$ ．把长为10m的梯子 $A B$ 斜靠在墙上，梯子底端离墙角6m．如果梯子的顶端下滑了2m，求梯子底部在水平方向滑动的距离BD．

查看试题解析
18. 如图，点 $M ， N$ 分别在 $∠ A O B$ 的边 $O A ， O B$ 上．请以 $M N$ 为底边作出等腰 $△ M N P$ ，且点P到 $∠ A O B$ 的两边的距离相等．（要求：用尺规作图，保留作图痕迹，不用写作法）

查看试题解析
19. 如图，已知点D、B在线段 $A E$ 上， $A D = B E$ ， $A C = D F$ ， $A C ∥ D F$ ．写出线段 $B C$ 与线段 $E F$ 平行的理由．

查看试题解析
20. 如图，∠AOP=∠BOP=15°，PC $∥$ OA，PD⊥OA，PE⊥OB，若PC=4，求PD的长．

查看试题解析
21. 如图，在四边形 $A B C D$ 中， $∠ B = ∠ C = 90 ° ， A B = A D = 24 c m ， B C = 16 c m ， C D = 8 c m$ ，E为 $B C$ 上一点．将四边形沿 $A E$ 折叠，使点 $B ， D$ 重合，求折痕 $A E$ 的长．

查看试题解析
22. 如图，在 $△ A B C$ 中， $B D ⊥ A C$ ， $C E ⊥ A B$ ，垂足分别为点D，E， $B D$ 与 $C E$ 相交于点F．若点F在 $∠ B A C$ 的平分线上，判断 $△ A B C$ 的形状，并说明理由．

查看试题解析
23. 如图， $A D = A C ， A B = A E ， ∠ D A B = ∠ C A E$ ．

(1)、写出 $△ A D E$ 与 $△ A C B$ 全等的理由；

(2)、判断线段 $D F$ 与 $C F$ 的数量关系，并说明理由．

查看试题解析
24. 已知：点P是线段 $A C$ 上一点， $B P = D P$ ， $A B = 3 ， C D = 7$ ．

(1)、如图1，若 $∠ A = ∠ C = ∠ B P D = 90 °$ ，求 $A C$ 的长；

(2)、如图2，若 $∠ A = ∠ C = ∠ B P D \neq 90 °$ ，能否求出 $A C$ 的长？若能，求出 $A C$ 的长；若不能，说明理由．

查看试题解析