山东省青岛市市北区2022-2023学年八年级上学期期中数学试题

试卷更新日期：2022-11-15 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各数是无理数的是（）

A、 $- 1$ B、 $\sqrt{3}$ C、 $6.8$ D、 $\frac{13}{9}$

查看试题解析
2. 在平面直角坐标系中，点 $B (6 ， - 5)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 下列四组数能作为直角三角形三边长的是（）

A、0.1，0.2，0.3 B、1，1，2 C、10，24，26 D、 $3^{2}$ ， $4^{2}$ ， $5^{2}$

查看试题解析
4. 如图， $\sqrt{7}$ 在数轴上对应的点可能是（）

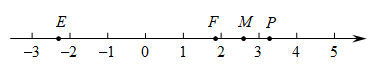A、点E B、点F C、点M D、点P

查看试题解析
5. 下列各点在一次函数 $y = 3 x - 2$ 的图象上的是（）

A、 $(2 ， 3)$ B、 $(0 ， 2)$ C、 $(- 2 ， 0)$ D、 $(3 ， 7)$

查看试题解析
6. 当 $a < - 1$ 时，代数式 $| 1 + a | - \sqrt{a^{2}}$ 的值为（）

A、 $- 1$ B、1 C、 $2 a + 1$ D、 $- 1 - 2 a$

查看试题解析
7. 如图，在“庆国庆，手拉手”活动中，某小组从营地A出发，沿北偏东 $53 °$ 方向走了1200m到达B点，然后再沿北偏西 $37 °$ 方向走了500m到达目的地C点，此时A，C两点之间的距离为（）

A、1000m B、1100m C、1200m D、1300m

查看试题解析
8. 已知正比例函数 $y = k x (k \neq 0)$ 的函数值y随x值的增大而增大，则一次函数 $y = - k x + 2$ 的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. $\sqrt{3}$ 的相反数是．

查看试题解析
10. 如图，等腰三角形 $A B C$ 的面积为．

查看试题解析
11. $2 m - 4$ 和 $6 - m$ 是正数a的两个平方根，则a的值为．

查看试题解析
12. 如图，将直线OA向上平移2个单位，得到一个一次函数的图象，则这个一次函数的表达式为.

查看试题解析
13. 若点 $A (- 3 ， y_{1})$ ， $B (2 ， y_{2})$ 都在一次函数 $y = - x + 1$ 的图象上，则 $y_{1}$ $y_{2}$ ．（填“ $>$ ”或“ $<$ ”）

查看试题解析
14. 如图，在平面直角坐标系中，等边三角形 $O B C$ 的边长为2，则点C关于x轴的对称点的坐标是．

查看试题解析
15. 已知点P在直线 $y = 2 x - 3$ 上，且点P到y轴的距离为1，则点P的坐标为．

查看试题解析
16. 如图已知长方形ABCD中AB=8cm，BC=10cm，在边CD上取一点E，将△ADE折叠使点D恰好落在BC边上的点F，则CE的长为.

查看试题解析

三、解答题

17. 计算

(1)、 $\frac{\sqrt{27} + \sqrt{3}}{\sqrt{3}} - 3$

(2)、 $\sqrt{12} + 2 \sqrt{48}$

(3)、 $(3 \sqrt{2} + \sqrt{5}) (3 \sqrt{2} - \sqrt{5})$

(4)、 $\sqrt{24} - 3 \sqrt{\frac{1}{6}} + \sqrt{6}$

查看试题解析
18. 某新建学校计划在一块面积为 $256 m^{2}$ 的正方形空地上建一个面积为 $150 m^{2}$ 的长方形花园（长方形花园的边与正方形空地的边平行），要求长方形花园的长是宽的2倍．请你通过计算说明该学校能否实现这个计划．

查看试题解析
19. 如图是中国象棋棋盘的一部分，棋子“马”走的规则是沿“日”形的对角线走，例如：图中“马”所在的位置可以直接走到点A或点B处，已知“帅”的坐标为 $(0 ， 0)$ ， A点的坐标为 $(- 2 ， 2)$ ．

(1)、“炮”的坐标为，点B的坐标为．

(2)、“马”从图中的位置出发，不走重复路线，按照“马走日”的规则，走两步后的落点与出发点间的最短距离为．

查看试题解析
20. 如图，在 $△ A B C$ 中，D为 $A B$ 边上一点，已知 $A C = 13$ ， $C D = 12$ ， $A D = 5$ ， $A B = B C$ ．请判断 $△ A C D$ 的形状，并求出 $B C$ 的长．

查看试题解析
21. 疫情防控人人有责，某学校需要购买的消毒液和医用口罩可在甲、乙两个商店买到．已知两个商店消毒液的标价都是每瓶25元，医用口罩的标价都是每包3元，但甲商场的优惠条件是：购买一瓶消毒液送一包医用口罩，其余医用口罩需原价购买；乙商场的优惠条件是：购买消毒液和医用口罩全部打八折，设该校一次性购买40瓶消毒液和m包医用口罩（ $m > 40$ ）的总费用为y（元）．

(1)、分别写出到两个商场购买的总费用y与m之间的关系式；

(2)、当购买150包医用口罩时，选择哪家商店比较合算？请说明理由．

查看试题解析
22. 如图，在正方形网格中，每个小正方形的边长为1，格点三角形 $A B C$ （顶点是网格线的交点的三角形）的顶点A，B，C的坐标分别为 $A (- 1 ， 4)$ ， $B (- 2 ， 1)$ ， $C (1 ， 1)$ ．

(1)、请在如图所示的平面直角坐标系中画出 $△ A B C$ ， $△ A B C$ 的面积是；

(2)、在图中画出 $△ A B C$ 关于x轴对称的 $△ A_{1} B_{1} C_{1}$ ；

(3)、在平面直角坐标系中，对于点 $P (a ， b)$ ， $Q (c ， d)$ ，若点M的坐标为 $M (k a + k c ， k b + k d)$ ，则称点M为P，Q的“k”级融合点，如点 $P (3 ， - 4)$ ， $Q (1 ， 2)$ ，则点P，Q的“2”级融合点的坐标为： $(2 \times 3 + 2 \times 1 ， 2 \times (- 4) + 2 \times 2)$ ，即 $(8 ， - 4)$ ．若点 $A_{2}$ 为 $A_{1}$ ， $B_{1}$ 的“ $- 2$ ”级融合点，则点 $A_{2}$ 的坐标为．

(4)、若点H为B，C的“k”级融合点， $S_{△ B C H} = 6$ ，则k的值为．

查看试题解析
23. 如图，在平面直角坐标系中，一次函数 $y_{1} = x + 2$ 的图象与x轴，y轴分别交于点A、B， $y_{2} = - \frac{1}{3} x + b$ 的图象与x轴，y轴分别交于点D、E，且两个函数图象相交于点 $C (m ， 5)$ ．

(1)、填空：m= ， b=；

(2)、求 $△ A C D$ 的面积；

(3)、在线段 $A D$ 上是否存在一点M，使得 $△ A B M$ 的面积与四边形 $B M D C$ 的面积比为 $4 ： 21$ ？若存在，请求出点M的坐标；若不存在，请说明理由．

(4)、点P在线段 $A D$ 上，连接 $C P$ ，若 $△ A C P$ 是直角三角形，请直接写出所有符合条件的点P坐标．

查看试题解析